ieee浮点数与常规浮点数_浮点数如何工作

ieee浮点数与常规浮点数

It is a pesky fact that computers work in binary approximations while humans tend to think in terms of exact values. This is why, in your high school physics class, you may have experienced “rounding error” when computing intermediate numerical values in your solutions and why, if you open a python terminal and compute 0.1 * 3, you will get a weird result.¹

一个令人讨厌的事实是，计算机以二进制近似的方式工作，而人类则倾向于根据精确值进行思考。 这就是为什么在高中物理课上计算解决方案中的中间数值时，您可能会遇到“取整误差”的原因，并且，如果打开python终端并计算0.1 * 3，您会得到一个奇怪的结果。¹

>>> 0.1 + 0.1 + 0.1
0.30000000000000004

this makes floating point numbers an example of a leaky abstraction. Normally, python and numerical computing libraries like numpy or PyTorch handle this behind the scenes. But understanding the details can help you avoid otherwise unexpected errors and speed up many machine learning computations. For example, Google’s Tensor Processing Units (TPUs) use a modified floating point format to substantially improve computational efficiency while trying to maintain good results.

这使浮点数成为泄漏抽象的一个例子。 通常，python和数值计算库(例如numpy或PyTorch)在后台进行处理。 但是了解细节可以帮助您避免其他意外错误，并加快许多机器学习的计算速度。 例如，Google的Tensor处理单元(TPU)使用修改后的浮点格式，可以在试图保持良好结果的同时大幅提高计算效率。

In this article we’ll dig into the nuts and bolts of floating point numbers, cover the edge cases (numerical underflow and overflow), and close with applications: TPU’s bfloat16 format and HDR imaging. The main background assumed is that you understand how to count in binary, as well as how binary fractions work.

在本文中，我们将深入研究浮点数的基本原理，涵盖边缘情况(数字下溢和溢出)，并介绍以下应用程序：TPU的bfloat16格式和HDR成像。 假定的主要背景是您了解如何对二进制进行计数以及二进制分数的工作方式。

代表整数 (Representing Integers)

Let’s briefly review counting to 5 in binary: 0, 1, 10, 11, 100, 101. Got it? This is great for an unsigned integer; one which is never negative. For example, if we have an 8 bit unsigned integer, we can represent numbers between 00000000 and 11111111. In decimal, that’s between 0 and 2⁸-1=255. For example, most standard image formats are 8-bit color, which is why the “RGB” values go from 0 to 255.

让我们简要回顾一下以5表示的二进制数：0、1、10、11、100、101。知道吗？ 这对于无符号整数很有用; 永不消极的一种。 例如，如果我们有一个8位无符号整数，则可以表示介于00000000和11111111之间的数字。以十进制表示，则是介于0和2⁸-1= 255之间。 例如，大多数标准图像格式都是8位彩色，这就是为什么“ RGB”值从0到255的原因。

Note also that we would typically abbreviate this with a hexadecimal (base 16) representation: 0x00 to 0xFF. The 0x prefix means “this is a hex number”. The hexadecimal digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; so F is essentially short for the four bits “1111” (both 0xF and 1111 are 15 in base-10). Also 8 bits are a byte, so our number is a measly 1 byte. But we won’t focus too much on hexadecimal in this article.

还要注意，我们通常将其缩写为十六进制(基数为16)：0x00至0xFF。 0x前缀表示“这是一个十六进制数字”。 十六进制数字为0、1、2、3、4、5、6、7、8、9，A，B，C，D，E，F; 因此F本质上是四个位“ 1111”的缩写(0xF和1111在base-10中均为15)。 另外8位是一个字节，因此我们的数字仅为1个字节。 但是在本文中，我们不会过多地关注十六进制。

签名整数 (Signed Integers)

Now, you will notice that with an unsigned int, we can’t represent simple numbers like -2. One way you could try to solve this is to make the first bit represent the sign. Say “0” means negative and “1” means positive. Thinking about 4-bit numbers, 0111 would be -7, while 1111 would be +7. However, this has some weird features. For example, 0000 is “-0” while 1000 is “+0”. This is not great: comparing two numbers for equality would get tricky; plus we are wasting space.

现在，您会注意到，对于无符号int，我们无法表示简单的数字，如-2。 您可以尝试解决此问题的一种方法是使第一位代表符号。 说“ 0”表示负数，“ 1”表示正数。 考虑4位数字，0111将为-7，而1111将为+7。 但是，这具有一些奇怪的功能。 例如，0000是“ -0”，而1000是“ +0”。 这不是很好：比较两个数字是否相等会很棘手； 再加上我们在浪费空间。

The standard solution to this is to use Two’s Complement, which is what most implementations use for signed integers. (There is also a little-used One’s Complement). However, this isn’t what we are going to need for floating point numbers, so we won’t delve into it.

对此的标准解决方案是使用Two's Complement ，这是大多数实现用于有符号整数的方式。 (还有一个很少使用的“补语” )。 但是，这不是浮点数所需的，因此我们不会深入研究。

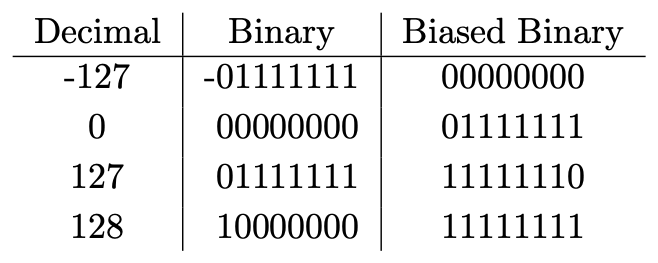
Let’s consider instead a biased representation of a signed 8-bit integer. It’s biased because, well it’s off by a bit. Instead of letting 00000000 represent 0, we will instead use 01111111 to represent 0. This would normally represent 127 in base 10. But we have biased our representation by 127. That means that 00000000 represents –127, while 11111111 represents 128.

让我们考虑一下带符号的8位整数的有偏表示。 这是有偏见的，因为它有点偏离了。 我们将使用01111111表示0，而不是使00000000表示0。通常在基数10中表示127。但是我们将表示形式偏斜了127。这意味着00000000表示–127，而11111111表示128。

双精度浮点数 (Double Precision Floating Point Numbers)

Since most recently produced personal computers use a 64 bit processor, it’s pretty common for the default floating-point implementation to be 64 bit. This is called “double precision” because it is double of the previous-standard 32-bit precision (common computers switched to 64 bit processors sometime in the last decade).

由于最新生产的个人计算机使用64位处理器，因此默认浮点实现是64位是很常见的。 之所以称其为“双精度”，是因为它是以前标准的32位精度的两倍(过去十年中的某个时候，普通计算机切换到64位处理器)。

科学计数法 (Scientific Notation)

For context, the basic idea of a floating point number is to use the binary-equivalent of scientific notation. Your high-school science teachers hopefully drilled into you exactly how to do this (along with a whole bunch about those dreaded signficant figures – sigfigs). For example, the scientific representation of 8191.31 is:

对于上下文，浮点数的基本思想是使用科学计数法的二进制等效项。 希望您的高中理科老师深入研究您的操作方法(以及有关那些令人恐惧的重要人物-sigfigs)。 例如，8191.31的科学表示为：

Scientific Notation for a Miscellaneous Decimal Number

十进制小数的科学计数法

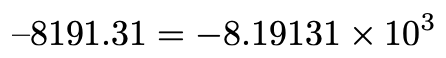
You should notice three key elements. First, a sign (is the number + or -?). Second, we always write the number with a single digit (between 1 and 9 inclusive), followed by a decimal point, followed by a number of digits. Compare that to the below, which are not in scientific notation even though they are true mathematical facts.

您应该注意到三个关键要素。 首先，一个符号(数字为+或-？)。 其次，我们总是用一个数字写数字(1到9之间，包括1和9)，然后是小数点，然后是数字。 将其与以下内容进行比较，尽管它们是真实的数学事实，但它们都不是科学符号 。

Representations NOT in Scientific Notation

表示形式不是科学计数法

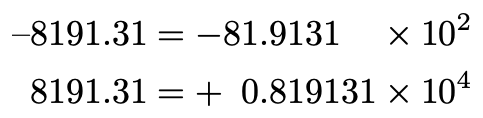
With that in mind, let’s think about what will change when we go to binary. First of all, instead of using 10 as the base of the exponent (also called the radix), we’ll want to use 2. Secondly, instead of decimal fractions, we’ll want to use binary fractions.

考虑到这一点，让我们考虑一下当使用二进制文件时会发生什么变化。 首先，我们要使用2，而不是使用10作为指数的基数(也称为基数)。其次，我们要使用二进制分数，而不是十进制分数。

Binary versus Decimal Scientific Notation

二进制与十进制科学计数法

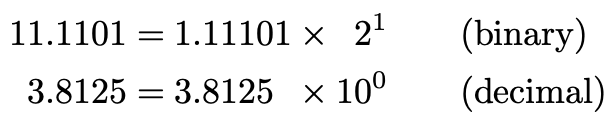
Please note that I have chosen to write the radix (2 or 10) and their exponents (1 or 0 respectively) in their decimal forms while the numbers on the left hand side and the significands are in binary or decimal respectively.

请注意，我选择以小数形式写基数(2或10)和指数(分别为1或0)，而左侧的数字和有效数字分别以二进制或十进制表示。

The binary number 1101 is 13 in base 10. And 13/16 is 0.8125. This is a binary fraction. If you haven’t played with these yet, you should convince yourself of the following:

二进制数1101在基数10中为13。13/ 16为0.8125。 这是二进制分数。 如果您还没有玩过这些，则应该使自己信服以下内容：

Some simple binary fractions

一些简单的二进制分数

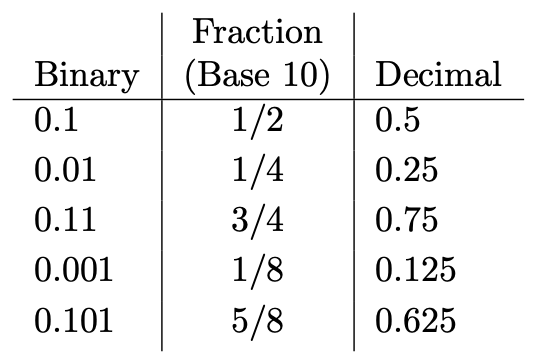
This is the binary version of the fact that 0.3 is 3/10 and 0.55 is 55/100 (which can be further simplified, of course).

这是以下事实的二进制形式：0.3是3/10，而0.55是55/100(当然，可以进一步简化)。

Great. We are now ready to dig into the details of floating point numbers.

大。 现在，我们准备深入研究浮点数。

IEEE 754标准 (The IEEE 754 Standard)

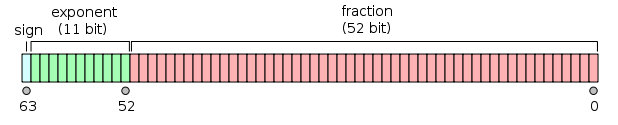
Here is the diagram for the “IEEE 754” standard commonly implemented. The first bit is the sign. 0 is positive and 1 is negative (the opposite of what we naïvely suggested above). There are 11 bits for the exponent and 52 or 53 (depending how you count) bits for the fraction, also called the “mantissa” or “significand”. The sign just works like the flag we saw above, so we’ll go into each of the last two in some depth.

这是通常实现的“ IEEE 754 ”标准的图表。 第一位是符号。 0是正数，而1是负数(与我们上面天真的建议相反)。 指数有11位，小数有52或53(取决于计数方式)位，也称为“尾数”或“有效位数”。 该标志的作用就像我们在上面看到的标志一样，因此我们将深入探讨最后两个标志。

Wikipedia) Wikipedia )

指数 (The Exponent)

The exponent is an 11-bit biased (signed) integer like we saw before, but with some caveats. The bias is 2¹⁰–1=1023, so that the 11 bits 01111111111 represent 0.

指数是一个11位有偏(有符号)整数，就像我们之前看到的一样，但有一些警告。 偏差为2 11-1 = 1023，因此11位01111111111表示0。

This would normally mean that the largest possible exponent is represented by the 11 bits 11111111111 (representing 2¹¹–1–1023=1024) and the smallest possible exponent is represented by the 11 bits 00000000000 (representing –1023).

这通常意味着，最大的可能指数由11个位11111111111(表示2 11-1–1023 = 1024)表示，最小的可能指数由11个位00000000000(表示–1023)表示。

However, as we will discuss:

但是，正如我们将要讨论的：

• The exponent represented by 11111111111 is reserved for infinities and NaNs.
  11111111111表示的指数保留给无限性和NaN。
• The 00000000000 exponent is reserved for representing 0 and something else we’ll get to.
  00000000000指数保留用于表示0以及我们将要达到的其他目标。

This means that the exponent can, in normal circumstances, be between –1022 and 1023 (2046 possible values).

这意味着在正常情况下，指数可以介于–1022和1023之间(可能为2046个值)。

重要意义 (The Significand)

The 52-bit significand represents a binary fraction. If you review the scientific notation section above, you’ll see that whenever we write a binary number in “binary scientific notation,” the leading digit is always 1. (In base 10 it could be between 1 and 9, but 2–9 aren’t binary digits). Since we know the leading digit will always be 1 (with some caveats to be discussed), we don’t need to actually store it on the computer (this would be wasteful). This is why I said the significand is 53 bits “depending on how you count.”

52位有效数字表示二进制分数。 如果您查看上面的科学计数法部分，您会发现，只要我们以“二进制科学计数法”编写二进制数，则前导数字始终为1。(以10为基数，它可能在1到9之间，但在2–9之间不是二进制数字)。 由于我们知道前导数字将始终为1(有一些注意事项需要讨论)，因此我们不需要将其实际存储在计算机上(这很浪费)。 这就是为什么我说有效位数是53位，“取决于您的计数方式”。

In other words, the 52 bits stored on the computer represent the 52 bits that come after the decimal point (or maybe we should call it a “binary point”). A leading 1 is always assumed.

换句话说，计算机上存储的52位代表小数点后的52位(或者也许我们应该称其为“二进制点”)。 始终假定前导1。

普通数字 (Normal Numbers)

I keep mentioning some caveats, and I intend to put them off for as long as possible. A “normal number” is a non-zero number that doesn’t use any of these caveats, and we are in a position to give some examples.

我一直在提一些警告，我打算尽可能拖延它们。 “正常数”是一个不为零的非零数字，我们可以举一些例子。

Recall the three components:

回忆一下三个组成部分：

• 1 bit for the sign
  1位符号
• 11 bits for the exponent, which is (in decimal) between –1022 and +1023. It is represented as a biased integer in the binary encoding.
  指数的11位，在–1022和+1023之间(十进制)。 它在二进制编码中表示为有偏整数。
• 52 bits for the significand.
  有效位为52位。

How would we represent the decimal number 1?

我们将如何表示十进制数字1？

Well, the sign is positive, so the sign bit is 0. (Think of 1 as a flag for “negative”). The exponent is 0. Remembering that the biased representation means we add 1023, we get the binary representation 01111111111. Finally, all the fraction bits are 0. Easy:

好吧，符号为正，所以符号位为0。(将1视为“负”的标志)。 指数为0。请记住，有偏表示表示我们加1023，得到二进制表示01111111111。最后，所有分数位均为0。简便：

Floating-Point Representation of 1

浮点表示形式1

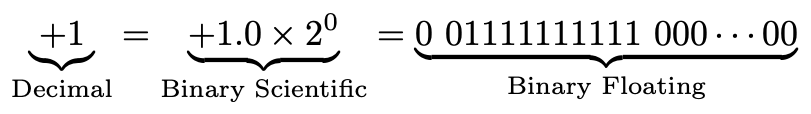
I’ve written the binary floating-point representation with a space separating the three parts. As usual, the radix and exponent in the “binary scientific” representation are actually in base 10.

我编写了二进制浮点表示，并用空格分隔了三个部分。 像往常一样，“二进制科学”表示形式中的基数和指数实际上位于基数10中。

What about a harder example, like 3? 3 is 1.5 times 2 (in decimal), so turning that into a binary fraction, we have 1.1. The exponent 2¹ is represented as 10000000000 accounting for bias.

像3这样的更难的例子呢？ 3是1.5乘以2(十进制)，因此将其转换为二进制分数，得到1.1。 代表偏差的指数2¹表示为10000000000。

What’s the largest (normal) number we can get? We should make the exponent 11111111110 (we can’t make it all ones, that’s reserved), which in decimal is 1023.

我们可以获得的最大(正常)数字是多少？ 我们应该将指数设为11111111110(不能全部保留，这是保留的)，十进制为1023。

The Maximum Floating Point Value

最大浮点值

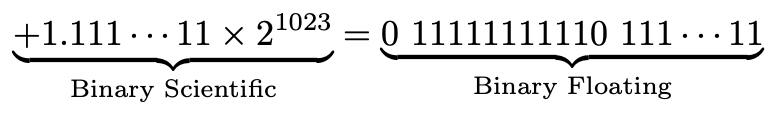
We can compute this:

我们可以计算出：

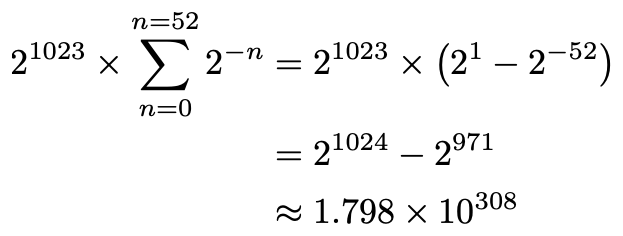
but we can also take advantage of the fact that Python has native arbitrary-precision integer arithmetic to gratuitously write out all 309 digits in base 10:

但是我们还可以利用Python具有本机任意精度整数算术来免费写出以10为底的所有309位的事实：

>>> 2 ** 1024 - 2 ** 971179769313486231570814527423731704356798070567525844996598917476803157260780028538760589558632766878171540458953514382464234321326889464182768467546703537516986049910576551282076245490090389328944075868508455133942304583236903222948165808559332123348274797826204144723168738177180919299881250404026184124858368

The smallest possible float is just the negative of this. But what is the smallest positive (normal) float? We already said the smallest positive exponent is –1022. Make the significand all 0s, and that means the smallest positive normal floating point number is:

最小的浮点数就是这个的负数。 但是最小的正(正常)浮点数是多少？ 我们已经说过最小的正指数是–1022。 使有效位全为0，这意味着最小的正法向浮点数为：

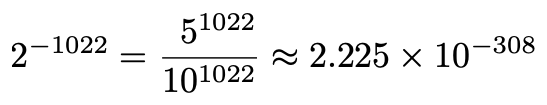
Again, arbitrary precision integer arithmetic means we can exploit the middle fraction to easily get an exact decimal value in all its glory.

再次，任意精度整数算术意味着我们可以利用中间分数轻松地获得所有精度的精确十进制值。

>>> numerator = 5 ** 1022
>>> print('0', str(numerator).rjust(1022, '0'), sep='.')0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002225073858507201383090232717332404064219215980462331830553327416887204434813918195854283159012511020564067339731035811005152434161553460108856012385377718821130777993532002330479610147442583636071921565046942503734208375250806650616658158948720491179968591639648500635908770118304874799780887753749949451580451605050915399856582470818645113537935804992115981085766051992433352114352390148795699609591288891602992641511063466313393663477586513029371762047325631781485664350872122828637642044846811407613911477062801689853244110024161447421618567166150540154285084716752901903161322778896729707373123334086988983175067838846926092773977972858659654941091369095406136467568702398678315290680984617210924625396728515625

You know, just in case you were curious. By the way, you can check all of this on your python + hardware setup with:

你知道，以防万一你好奇。 顺便说一句，您可以使用以下命令在python +硬件设置上检查所有这些：

>>> import sys
>>> sys.float_infosys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)

and essentially every other programming language has a similar feature.

基本上所有其他编程语言都具有类似的功能。

无限和NaN (Infinities and NaNs)

Okay, here’s where things get weird. If all of the exponent bits are 1, then the number represented is either infinite or not a number (NaN):

好的，这是奇怪的地方。 如果所有指数位均为1，则表示的数字为无限或不是数字(NaN)：

• If the fraction bits are all 0, the number is infinite. The sign bit controls whether it is –∞ or +∞.
  如果小数位全为0，则数字为无限。 符号位控制它是–∞还是+∞。
• If the fraction bits are not all 0, the “number” is not a number (NaN). Depending on the first bit it can be either a quiet NaN or a signaling NaN. a quiet NaN propagates (add another number to it and you just get NaN). A signaling NaN is supposed to “throw an error”, roughly speaking.² The remaining bits are typically not used.
  如果分数位不全为0，则“数字”不是数字(NaN)。 根据第一位，它可以是安静的NaN或信令NaN。 安静的NaN传播(向其添加另一个数字，您将得到NaN)。 粗略地说，信号NaN应该“引发错误”。²通常不使用其余位。

The thing I initially found surprising about this is that this is a hardware implementation on commonly used chips. This means, for example, you can use it on a GPU. Why would you want to do that? Well, consider the convenient fact that e to the power of –∞ is 0.

最初使我感到惊讶的是，这是在常用芯片上的硬件实现。 例如，这意味着您可以在GPU上使用它。 你为什么想这么做？ 好吧，考虑一个方便的事实，即–∞的幂的e为0。

>>> from math import exp
>>> minus_infinity = float('-inf')
>>> exp(minus_infinity)0.0

In the paper that introduced the transformer architecture for NLP tasks (the one used by BERT, GPT-2, and their more recent cousins), the training was autoregressive which meant that in the attention module’s softmax layers, certain outputs were required to be 0. But if you look at the formula for the softmax and recall that your high school math teacher told you that “there is no number such that exponentiating to it is 0,” you will see it’s tricky to make a softmax return 0. Unless of course, you make (minus) infinity a number!

在介绍用于NLP任务的变压器架构 (由BERT，GPT-2及其最近的堂兄使用的变压器 )的论文中，训练是自回归的，这意味着在关注模块的softmax层中，某些输出必须为0 。但是，如果您查看softmax的公式，并回想起您的高中数学老师告诉您“没有数字可以使它的幂为0，”您将发现使softmax返回0是很棘手的。当然，您使(负)无穷大！

And, crucially, this is a hardware implementation. If it was a gimmicky Python (or PyTorch, or Numpy) workaround that represented numbers as an object which might sometimes contain a floating point number, this would substantially slow down numerical computations.

而且，至关重要的是，这是一种硬件实现。 如果这是个花哨的Python(或PyTorch或Numpy)解决方法，将数字表示为有时可能包含浮点数的对象，则这将大大减慢数值计算的速度。

Also, the unending complexity of computer hardware is always impressive.

而且，计算机硬件的无限复杂性总是令人印象深刻。

零 (Zero)

But wait, there’s more! We haven’t even described how to represent 0 yet. Using our exponents and our fraction bits, we were only able to make a very small positive number, not actually 0. The solution of course is that if the exponent bits are all 0 and so is the fraction, then the number is 0. In other words, if the exponent bits are 00000000000 and the fraction bits are also all zeros. Note this means that 0 is “signed” – there is both +0 and –0. In Python, they are stored differently, but they are equal to each other.

但是，等等，还有更多！ 我们甚至还没有描述如何表示0。 使用我们的指数和分数位，我们只能得出一个很小的正数，实际上不是0。解决方案是，如果指数位都为0，分数都为零，则数字为0。换句话说，如果指数位是00000000000，而小数位也都是零。 请注意，这意味着0是“有符号的” –同时存在+0和–0。 在Python中，它们的存储方式不同，但是彼此相等。

>>> zero = 0.0
>>> print(zero, -zero)0.0 -0.0>>> zero == -zeroTrue

There are a few edge cases where things get weird though. When trying to compute an angle with atan2, you will see that they are in fact represented differently:

在一些极端情况下，事情变得怪异。 尝试使用atan2计算角度时，您会发现它们实际上以不同的方式表示：

>>> from math import atan2
>>> zero = 0.0
>>> print(atan2(zero,  zero), 
>>>       atan2(zero, -zero))0.0 3.141592653589793

次正规数 (Subnormal Numbers)

The final case to cover is when all the exponent bits are 0, but the fraction bits are not 0. If we have a representation that doesn’t use some possible bit sequences, we are wasting space. So why not use it to represent even smaller numbers? These numbers are called subnormal (or denormal) numbers.

最后要讨论的情况是所有指数位均为0，但分数位不为0。如果我们有一个不使用某些可能的位序列的表示形式，那是在浪费空间。 那么，为什么不使用它来代表更小的数字呢？ 这些数字称为非正规(或非正规)数字。

Basically, the rule is that the exponent is still considered to have its minimal value (–1022) and instead of our “binary scientific” notation always starting with a 1 (as in 1.001), we assume instead that it starts with a 0. So we can have 0.001 times 2 to the power of –1022. This lets us represent numbers up with an exponent 52 less (as small as –1074). Thus:

基本上，该规则是，该指数仍被认为具有最小值(–1022)，而不是总是以1(如1.001)开头的“二进制科学”表示法，而是假定它以0开头。因此，我们可以得到–1022的幂的0.001乘2。 这使我们可以用减少52的指数(小至–1074)来表示数字。 从而：

>>> 2 ** -1074
5e-324>>> 2 ** -1075
0.0>>> 2 ** -1075 == 0
True

The benefits of subnormal numbers are that, when you subtract two different normal floats, you are guaranteed to get a non-zero result. The cost is lost precision (there is no precision stored in the leading 0s – remember how sigfigs work?). This is called gradual underflow. As floats get smaller and smaller, they gradually lose precision.

次普通数的好处是，当您减去两个不同的普通浮点数时，可以保证得到一个非零的结果。 代价是失去了精度(前导0中没有精度存储–请记住sigfigs是如何工作的？)。 这称为逐渐下溢 。 随着浮子越来越小，它们逐渐失去精度。

Without subnormal numbers you would have to flush to zero, losing all your precision at once and significantly increasing the chance that you’ll accidentally end up dividing by 0. However, subnormal numbers significantly slow down calculations.

如果没有低于标准的数字，您将不得不冲洗为零 ，立即失去所有精度，并显着增加了意外地将结果除以0的机会。但是，低于标准的数字会大大降低计算速度。

应用领域 (Applications)

Okay, we spent all this time talking about floating point numbers. Besides some weird edge case about 0.1 * 3 that never really comes up, who cares?

好的，我们一直都在谈论浮点数。 除了一些从未真正出现过的怪异的边缘情况(约0.1 * 3)，谁在乎呢？

张量处理单元(TPU) (Tensor Processing Units (TPUs))

Besides the 64-bit float we explored at length, there are also 32-bit floats (single precision) and 16-bit floats (half-precision) commonly available. PyTorch and other numerical computing libraries tend to stick to 32-bit floats by default. Half the size means the computations can be done faster (half as many bits to crunch).

除了我们详细探讨的64位浮点数之外，还有通常可用的32位浮点数(单精度)和16位浮点数(半精度)。 PyTorch和其他数值计算库在默认情况下倾向于使用32位浮点数。 一半的大小意味着可以更快地完成计算(要处理的位数减少一半)。

But lower precision comes with a cost. With a standard half-precision float (5 exponent bits, 10 significand bits), the smallest number bigger than 1 is about 1.001. You can’t represent the integer 2049 (you have to pick either 2050 or 2048; and no decimals in between either). 65535 is the largest possible number (or close, depending on precise implementation details).

但是降低精度需要付出代价。 对于标准的半精度浮点数(5个指数位，10个有效位位)，最小的数字大于1约为1.001。 您不能代表2049整数(您必须选择2050或2048；并且两者之间都不能选择小数)。 65535是最大数目(或接近，取决于精确的实现细节)。

Google’s Tensor Processing Units instead use a modified 16-bit format for multiplication as part of their many optimizations for deep-learning tasks. The 8-bit exponent with 7-bit significand has just as many exponent bits as a 32-bit floating point number. And it turns out that in deep learning applications, this matters more than the significand bits. Also, when multiplying, the exponents can be added (easy) while the significand bits have to be multiplied (harder). Making the significand smaller makes the silicon that multiplies floats about 8 times smaller.

Google的Tensor处理单元使用经过修改的16位格式进行乘法运算，这是其针对深度学习任务进行的许多优化措施的一部分。 具有7位有效数字的8位指数具有与32位浮点数一样多的指数位。 事实证明，在深度学习应用程序中，这比有效位更为重要。 同样，在相乘时，可以将指数相加(容易)，而有效位必须相乘(更难)。 减小有效位数会使相乘的硅浮子小8倍左右。

Plus, the TPU float format flushes to zero instead of using subnormal numbers to boost speed.

另外，TPU浮点格式将刷新为零，而不是使用次标准数来提高速度。

高动态范围(HDR)图像 (High Dynamic Range (HDR) Images)

If you read the Google blog post about their custom 16-bit float format, you’ll see they talk about “dynamic range.” In fact, this something similar is going on with HDR images (like the ones you can capture on your phone).

如果您阅读有关其自定义16位浮点格式的Google 博客文章 ，就会发现他们谈论的是“动态范围”。 实际上，HDR图像(例如您可以在手机上捕获的图像)正在发生类似的情况。

A standard image uses an 8-bit RGB encoding. Those 8 bits represent an unsigned integer between 0 and 255. The problem with this is that the relative precision (% jump between consecutive values) is much worse when it’s darker. For example, between a (decimal) pixel value of 10 and 11, there is a 10% jump! But for bright values, the relative difference between 250 and 251 is just 0.4%.

标准图像使用8位RGB编码。 这8位代表0到255之间的无符号整数。问题在于，相对精度(连续值之间的百分比跳变)在较暗时会更差。 例如，在(十进制)像素值10和11之间，存在10％的跳变！ 但是对于明亮的值，250和251之间的相对差仅为0.4％。

Now the human eye is more sensitive to changes in brightness with dark tones than with bright ones. Meaning the fixed-precision representation is the opposite of what we’d want. Thus, a standard digital or phone camera shooting a JPEG or similar adjusts its sensitivity by recording relatively more precision in the darker tones using a gamma encoding.

现在，人眼对暗色调的亮度变化比对亮色调更敏感。 意思是固定精度表示与我们想要的相反。 因此，拍摄JPEG或类似图像的标准数码相机或电话相机通过使用伽玛编码以较暗的色调记录相对较高的精度来调整其灵敏度。

The downside to this is that, even if you add bits (say with a 16-bit RBG image), you don’t necessarily gain as much precision in the parts of your image that are bright.

不利的一面是，即使您添加位(例如使用16位RBG图像)，也不一定会在图像的明亮部分获得太多的精度。

So, an HDR image uses floating point numbers to represent the pixels! This allows a high “dynamic” range (the exponent can be high or low) while still maintaining relative precision across all brightness scales. Perfect for keeping the data from scenes with high contrast. For example in the Radiance HDR format, the exponent is shared across the three colors (channels) in each pixel.

因此，HDR图像使用浮点数表示像素！ 这样可以实现较高的“动态”范围(指数可以高或低)，同时在所有亮度范围内仍保持相对精度。 完美保留高对比度场景中的数据。 例如，在“ 辐射HDR”格式中，指数在每个像素的三种颜色(通道)之间共享。

结论 (Conclusion)

This might be more than you ever wanted to know about floating point numbers. With any luck, you won’t encounter too much numerical under-flow or over-flow that can’t be solved with a simple log-sum-exp or arbitrary-precision integers. But if you do, you’ll be well-prepared! Hopefully, you are also well-positioned to think about just how much precision you need in your machine-learning models as well.

这可能比您想了解的浮点数更多。 幸运的是，您不会遇到太多的数字下溢或上溢，而用简单的log-sum-exp或任意精度的整数则无法解决。 但是，如果这样做，您将做好充分的准备！ 希望您也有能力考虑一下在机器学习模型中还需要多少精度。

笔记 (Notes)

[1] Note: this article assumes a relatively standard setup. It is possible (though uncommon) your results could differ depending on your hardware and software implementation.

[1]注意：本文假设使用相对标准的设置。 根据硬件和软件的实现，结果可能(尽管不常见)可能有所不同。

[2] I mean, you Python interpreter is allowed to throw an error, crash, and then stop doing things. Your CPU can’t do that exactly: it has to stay alive.

[2]我的意思是，您允许Python解释器引发错误，崩溃并停止运行。 您的CPU无法完全做到这一点：它必须保持生命。

翻译自: https://towardsdatascience.com/how-floating-point-numbers-work-1429907b6d1d

ieee浮点数与常规浮点数