为什么随机性是信息-CSDN博客

用位思考 (Thinking in terms of Bits)

Imagine you want to send outcomes of 3 coin flips to your friend's house. Your friend knows that you want to send him those messages but all he can do is get the answer of Yes/No questions arranged by him. Let's assume the arranged question: Is it head? You will send him the sequence of zeros or ones as an answer to those questions which is commonly known as a bit(binary digit). If Zero represents No and one represents Yes and the actual outcome of the toss was Head, Head, and Tail. Then you would need to send him 1 1 0 to convey your facts(information). so it costs us 3 bits to send those messages.

我想像一下，您想将3次硬币翻转的结果发送到您朋友的房子。您的朋友知道您想向他发送这些消息，但是他所能做的就是得到他安排的是/否问题的答案。让我们假设一个安排好的问题：是头吗？您将把零或一的序列发送给他，作为对这些问题的解答(通常称为位(二进制数字))。如果零代表否，一个代表是，并且折腾的实际结果是头，头和尾。然后，您需要向他发送1 1 0来传达您的事实(信息)。因此发送这些消息要花费我们3位。

How many bits does it take to make humans?

做一个人需要多少位？

Our entire genetic code is contained in a sequence of 4 states T, A, G, C in DNA. Now we would need 2 bits (00,01,10,11) to encode these states. And multiplied by 6 billion letters of genetic code in the genome yields 1.5 GB of information. So we can fit our entire genetic code on a single DVD.

我们的整个遗传密码包含在DNA的4种状态T，A，G，C中。现在我们将需要2位(00,01,10,11)来编码这些状态。乘以基因组中60亿个字母的遗传密码可产生1.5 GB的信息。因此，我们可以将整个遗传密码放在一张DVD中。

多少信息？ (How much Information?)

Suppose I flip a fair coin with a 50% chance of getting head and a 50% chance of getting tails. Similarly now instead of a fair coin, I flip a biased coin with head on both sides. What do you think in which case I am more certain about the outcome of the toss? Obviously the answer would be a biased coin. It is because in the case of the fair coin I am uncertain about the outcome because none of the possibilities are more likely to happen than the other while in biased coin I am not uncertain about the outcome because I know I will get heads.

小号 uppose我翻转一个公平的硬币获得头部的几率为50％和获得尾巴的几率为50％。现在，类似地，我用偏头硬币在两头都翻转而不是公平的硬币。在这种情况下，您认为我对投掷的结果有何把握？答案显然是有偏见的。这是因为在公平硬币的情况下，我不确定结果，因为没有一种可能性比另一种可能性更大；而在有偏见的硬币中，我不确定结果，因为我知道我会获得正面的。

Let's look at the other way. Would you be surprised if I told you the coin with head on both sides gave head as an outcome? No. Because you did not learn anything new with that statement. Outcomes did not give you any further information. On the other hand, when the coin is fair you have the least knowledge of what will happen next. So each toss gives you the new information.

让我们看看另一种方式。如果我告诉您两侧都带硬币的硬币作为结果给了您，您会感到惊讶吗？不。因为您没有从该声明中学到任何新知识。结果未提供任何进一步的信息。另一方面，当代币公平时，您对接下来将要发生的事情的了解最少。因此，每次折腾都会为您提供新的信息。

So the intuition behind quantifying information is the idea of measuring how much surprise there is in an event. Those events that are rare (low probability) are more surprising and therefore have more information than those events that are common (high probability).

因此，量化信息背后的直觉是测量事件中有多少惊喜的想法。那些罕见的事件(低概率)比那些常见的事件(高概率)更令人惊讶，因此具有更多的信息。

Low Probability Event: High Information (surprising)

低概率事件 ：高信息( 令人惊讶)

High Probability Event: Low Information (unsurprising)

高概率事件 ：低信息( 不足为奇 )

As a prereqisite, If you want to learn about basic probability theory, I wrote about that here.

作为先决条件，如果您想了解基本概率论，我在这里写过。

So information seems to be randomness. So if we want to know how much information does something contains we need to know how random and unpredictable it is. Mathematically, Information gained by observing an event X with probability P is given by:

因此，信息似乎是随机的。因此，如果我们想知道某物包含多少信息，就需要知道它是多么随机和不可预测。在数学上， 通过观察概率为P的事件X获得的信息由下式给出 ：

By plugging the values in the formula, we can clearly see information contained in certain events like observing head by tossing a coin with heads on both sides is 0 while the uncertain event leads to more information after it is observed. So this definition satisfies the basic requirement that it is a decreasing function of p.

通过插入公式中的值，我们可以清楚地看到某些事件中包含的信息，例如通过掷一个硬币，使硬币的正反两面都是正面，而观察正面，则不确定事件会导致更多信息。因此，该定义满足了它是p的递减函数的基本要求。

But You may have the question …………..

但是您可能有一个问题…………..

Why the logarithmic function?

为什么是对数函数？

And what is the base of the logarithm?

对数的底是什么？

As an answer to the second question, You can use any base of the logarithm. In information theory, we use base 2 in which case the unit of information is called a bit.

作为第二个问题的答案，您可以使用任何对数的底数。在信息论中，我们使用以2为底的情况，在这种情况下，信息的单位称为位。

The answer to the first question is that the resulting definition has several elegant resulting properties, and it is the simplest function that provides these properties. One of these properties is additivity. If you have two independent events (i.e., events that have nothing to do with each other), then the probability that they both occur is equal to the product of the probabilities with which they each occur. What we would like is for the corresponding information to add up.

第一个问题的答案是，生成的定义具有多个优美的生成属性，而这是提供这些属性的最简单函数。这些属性之一是可加性。如果您有两个独立的事件(即彼此无关的事件)，则它们都发生的概率等于它们各自发生的概率的乘积 。 我们希望将相应的信息加起来。

For instance, the event that it rained in Kathmandu yesterday and the event that the number of views in this post is independent, and if I am told something about both events, the amount of information I now have should be the sum of the information in being told individually of the occurrence of the two events.

例如，昨天在加德满都下雨的事件，以及该帖子中的视图数量是独立的事件，并且如果被告知有关这两个事件的信息，那么我现在拥有的信息量应该是被分别告知两个事件的发生。

The logarithmic definition provides us with the desired additivity because given two independent events A and B

对数定义为我们提供了所需的可加性，因为给定了两个独立的事件A和B

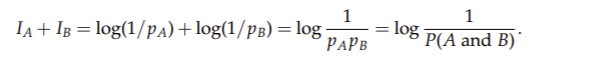
熵 (Entropy)

Entropy is the average(expected) amount of information conveyed by identifying the outcome of some random source.

Ëntropy是信息的平均(预期)量传送通过识别一些随机源的结果。

It is simply the sum of several terms, each of which is the information of a given event weighted by the probability of that event occurring.

它只是几项的总和，每一项都是给定事件的信息，由该事件发生的概率加权。

Like information, it is also measured in bits. If we use log2 for our calculation we can interpret entropy as the number of bits it would take us on average to encode our information.

像信息一样，它也以位为单位。如果我们使用l og 2进行计算，我们可以将熵解释为编码我们的信息平均需要的位数。

In the important special case of two mutually exclusive events (i.e., exactly one of the two events can occur), occurring with probabilities p and 1 − p, respectively, the entropy is:

在两个互斥事件的重要特殊情况下(即恰好可以发生两个事件之一)，它们分别以概率p和1-p发生，熵为：

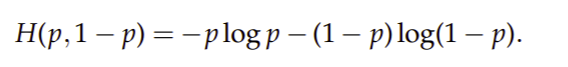
带走 (Takeaway)

Information is randomness. The more uncertain we are about the outcome of an event the more information we will get after observing an event.
信息就是随机性。我们对事件的结果越不确定，观察事件后我们将获得更多的信息。
The equation for calculating the range of Entropy: 0 ≤ Entropy ≤ log(n), where n is the number of outcomes
计算熵范围的公式：0≤熵≤log(n)，其中n是结果数
Entropy 0(minimum entropy) occurs when one of the probabilities is 1 and the rest are 0’s.
当其中一个概率为1且其余概率为0时，发生熵0(最小熵)。
Entropy log(n)(maximum entropy) occurs when all the probabilities have equal values of 1/n.
当所有概率都具有等于1 / n的值时，就会出现熵log(n)(最大熵)。