人工智能中的minimax算法

Algorithms can search the game trees to determine the best move to make from the current state. The most well known is called the Minimax algorithm. The minimax algorithm is a useful method for simple two-player games. It is a method for selecting the best move given an alternating game where each player opposes the other working toward a mutually exclusive goal. Each player knows the moves that are possible given a current game state, so for each move, all subsequent moves can be discovered.

一个lgorithms可以搜索游戏树来确定从当前状态做出最好的举动。 最著名的称为Minimax算法。 minimax算法是用于简单的两人游戏的有用方法。 在给定交替游戏的情况下，这是一种用于选择最佳移动的方法，其中，每个玩家都反对另一个玩家，朝着互斥目标努力。 每个玩家都知道在当前游戏状态下可能发生的移动，因此对于每个移动，都可以发现所有后续移动。

At each node in the tree (possible move) a value defining the goodness of the move toward the player winning the game can be provided. So at a given node, the child nodes (possible moves from this state in the game) each have an attribute defining the relative goodness of the move. It’s an easy task then to choose the best move given the current state. But given the alternating nature of two-player games, the next player makes a move that benefits them (and in zero-sum games, results in a deficit for the alternate player).

在树中的每个节点(可能的移动)上，可以提供一个值，该值定义了朝着赢得游戏的玩家的移动的良好性。 因此，在给定节点上，子节点(游戏中从该状态开始的可能移动)均具有定义移动相对优势的属性。 然后，根据当前状态选择最佳移动是一项容易的任务。 但是，鉴于两人游戏的交替性质，下一位玩家会采取有利于他们的举动(在零和游戏中，会导致另一位玩家出现亏损)。

The ply of a node is defined as the number of moves needed to reach the current state (game configuration). The ply of a game tree is then the maximum of the plies of all nodes.

节点的层数定义为达到当前状态(游戏配置)所需的移动次数。 那么，游戏树的层数就是所有节点的层数的最大值。

Minimax can use one of two basic strategies. In the first, the entire game tree is searched to the leaf nodes (end-games), and in the second, the tree is searched only to a predefined depth and then evaluated. Let’s now explore the minimax algorithm in greater detail.

Minimax可以使用两种基本策略之一。 首先，将整个游戏树搜索到叶子节点(最终游戏)，然后在第二步中，仅搜索树到预定深度，然后进行评估。 现在让我们更详细地研究minimax算法。

When we employ a strategy to restrict the search depth to a maximum number of nodes (do not search beyond N levels of the tree), the look ahead is restricted and we suffer from what is called the horizon effect. When we can’t see beyond the horizon, it becomes easier to make a move that looks good now, but leads to problems later as we move further into this subtree.

当我们采用一种策略来将搜索深度限制为最大数量的节点时(不要搜索超过树的N个层)，向前的视线就受到了限制，并且受到所谓的“水平效应”的影响。 当我们看不到视野之外时，现在进行看起来不错的移动变得容易，但是当我们进一步移入此子树时，则会导致问题。

Minimax is a depth-first search algorithm that maintains a minimum ora maximum value for successor nodes at each node that has children. Uponreaching a leaf node (or the max depth supported), the value of the nodeis calculated using an evaluation (or utility) function. Upon calculating anode’s utility, we propagate these values up to the parent node based onwhose move is to take place.

Minimax是一种深度优先搜索算法，该算法在具有子节点的每个节点上为后继节点保持最小值或最大值。 到达叶节点(或支持的最大深度)后，使用评估(或效用)函数计算该节点的值。 在计算阳极的效用后，我们根据发生的移动将这些值传播到父节点。

For our move, we’ll use the maximum value as our determiner for the best move to make. For our opponent, the minimum value is used.

对于我们的举动，我们将使用最大值作为确定最佳举动的决定因素。 对于我们的对手，使用最小值。

At each layer of the tree, the child nodes area is scanned anddepending on whose move is to come, the maximum value is kept (in the caseof our move), or the minimum value is kept (in the case of the opponent’smove). Since these values are propagated up in an alternating fashion, wemaximize the minimum, or minimize the maximum. In other words, weassume that each player makes the move next that benefits them the most.The basic algorithm for minimax is shown in the below figure 1.1.

在树的每一层，将扫描子节点区域，并根据要移动的对象来决定，保留最大值(对于我们的移动而言)，或保留最小值(对于对手的移动) 。 由于这些值以交替的方式向上传播，因此我们使最小值最大化或使最大值最小化。 换句话说，我们假设每个玩家接下来的动作都是对他们最大的好处。下图1.1显示了minimax的基本算法。

minimax游戏树搜索的基本算法： (Basic algorithm for minimax game tree search:)

minimax( player, board )if game_won( player, board ) return winfor each successor boardif (player == X) return maximum of successor boardsif (player == O) return minimum of successor boardsendend

minimax(player，board)if game_won(player，board)为每个后继boardif返回winif(player == X)返回后继boardif的最大值if(player == O)返回后继boardend的最小值

FIGURE 1.2: End-game tree for a game of Tic-Tac-Toe.

图1.2：井字游戏的最终游戏树。

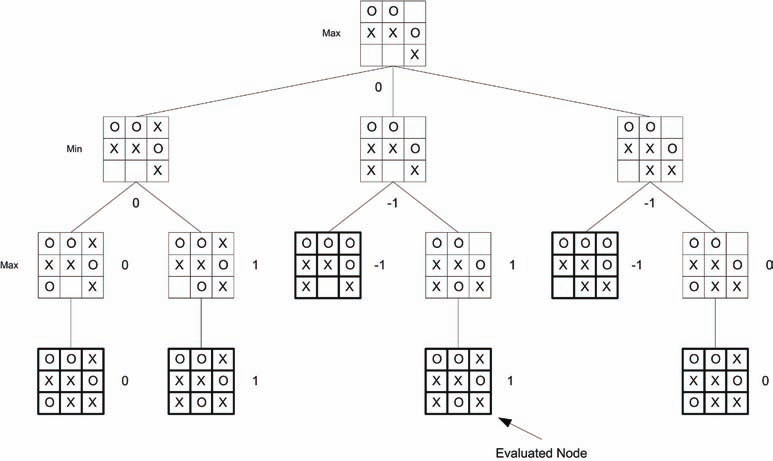
To understand this approach, look at the Figure 1.2. The end-game for a particular Tic-Tac-Toe board configuration. Both X and O have played three turns, and now it’s X’s turn. We traverse this tree in depth-first order, and upon reaching either a win/lose or draw position, we set the score for the board. We’ll use a simple representation here, -1 representing a loss, 0 for a draw, and 1 for a win. The boards with bold lines define the win/loss/ draw boards where the score is evaluated. When all leaf nodes have been evaluated, the node values can be propagated up based on the current player.

要了解这种方法，请查看图1.2。 特定Tic-Tac-Toe棋盘配置的最终游戏。 X和O都玩了三回合，现在是X的回合。 我们以深度优先的顺序遍历这棵树，并在到达赢/输或平局的位置上，确定棋盘的得分。 我们在这里使用简单的表示形式，-1表示亏损，0表示平局，1表示获胜。 带有粗线的棋盘定义了在其中评估得分的赢/输/平局。 评估完所有叶子节点后​​，可以根据当前播放器向上传播节点值。

At layer 2 in the game tree, it’s O’s turn, so we minimize the children and score the parent with the smallest value. At the far left portion of the game tree, the values 0 and 1 are present, so 0 is kept (the minimum) and stored in the parent. At layer 1 in the tree, we’re looking at the maximum, so out of node scores 0, -1, and -1, we keep 0 and store this at the parent (the root node of our game tree).

在游戏树的第2层，轮到O了，所以我们最小化子级，并以最小的值给父级评分。 在游戏树的最左侧，存在值0和1，因此保留0(最小值)并将其存储在父级中。 在树的第1层，我们正在查看最大值，因此在节点得分0，-1和-1中，我们保持0并将其存储在父级(游戏树的根节点)中。

With the scores having been propagated to the root, we can now make the best move possible. Since it’s our move, we’re maximizing, so we look for the node with the largest score (the left-most node with a value of 0), and we take this position. Our opponent (who is minimizing) then chooses the minimum node value (left-most node in tree depth 2). This leaves us with our final move, resulting in a draw.

随着分数传播到根源，我们现在可以采取最佳行动。 由于这是我们的举动，因此我们正在最大化，因此我们寻找得分最高的节点(最左边的节点，值为0)，然后采取此位置。 我们的对手(正在最小化)然后选择最小节点值(树深度2中最左侧的节点)。 这让我们留下了最后的一步，导致了平局。

Note that in a game where perfect information is available to each player, and no mistakes are made, the end-result will always be a draw. We’ll demonstrate a program to play Tic-Tac-Toe to show how this algorithm can be constructed. Like any tree algorithm, it can be built simply and efficiently using recursion.

请注意，在每个玩家都能获得完美信息且没有犯错误的游戏中，最终结果将始终是平局。 我们将演示一个播放井字游戏的程序，以演示如何构造该算法。 与任何树算法一样，可以使用递归简单有效地构建它。

An alternative to building the entire search tree is to reduce the depth of the search, which implies that we may not encounter leaf nodes. This is also known as an imperfect information game and can result in sub- optimal strategies of play. The advantage of reducing the search tree is that game play can occur much more quickly and minimax can be used for games of higher complexity (such as Chess or Checkers).

构建整个搜索树的另一种方法是减少搜索的深度，这意味着我们可能不会遇到叶节点。 这也被称为不完美的信息游戏，可能导致游戏策略不佳。 减少搜索树的优点是可以更快地进行游戏，并且minimax可以用于复杂程度较高的游戏(如国际象棋或西洋跳棋)。

Recursively searching an entire game tree can be a time (and space) consuming process. This means that minimax can be used on simple games such as Tic-Tac-Toe, but games such as Chess are far too complex to build an entire search tree. The number of board configurations for Tic-Tac-Toe is around 24,683. Chess is estimated to have on the order of 10 100 board configurations a truly massive number.

递归搜索整个游戏树可能是一个耗时(和空间)的过程。 这意味着minimax可以用于诸如井字游戏之类的简单游戏，但是诸如国际象棋之类的游戏过于复杂而无法构建整个搜索树。 井字游戏的板配置数量约为24,683。 据估计，国际象棋有大约10100种电路板配置，数量确实很多。

翻译自: https://medium.com/ai-in-plain-english/the-minimax-algorithm-in-artificial-intelligence-a6f0f108cc38