不相交集adt_不相交集联合发现

最新推荐文章于 2024-11-13 17:26:18 发布

weixin_26728245

最新推荐文章于 2024-11-13 17:26:18 发布

阅读量162

点赞数

文章标签： python

原文链接：https://medium.com/@shawnlyu.official/disjoint-set-union-find-ce1935b197d2

版权

不相交集adt

Source: https://shawnlyu.com/algorithms/disjoint-set-union-find/

资料来源： https : //shawnlyu.com/algorithms/disjoint-set-union-find/

In computer science, a disjoint-set data structure … is a data structure that stores a collection of disjoint (non-overlapping) sets. … It provides operations for adding new sets, merging sets (replacing them by their union), and finding a representative member of a set.

在计算机科学中，不相交集数据结构…是一种存储不相交(不重叠)集的集合的数据结构。 ......它提供了操作添加新集，合并组(由他们代替他们的工会)，并找到一组有代表性的成员。

Source: https://en.wikipedia.org/wiki/Disjoint-set_data_structure

资料来源： https : //en.wikipedia.org/wiki/Disjoint-set_data_structure

Disjoint Set helps to group distinct elements into a collection of disjoint sets. There are two major functions associated with it: finding the set that a given element belongs to and merging two sets into one (Cormen, Thomas H., and Thomas H. Cormen. Introduction to Algorithms). This post will introduce the implementations of two functions union(u,v) and find(p), and provide more details using Leetcode 200. Number of Islands as an example.

不相交集有助于将不同的元素分组为不相交集的集合。与之关联的主要功能有两个：查找给定元素所属的集合，并将两个集合合并为一个集合(Cormen，Thomas H.和Thomas H. Cormen。算法介绍)。这篇文章将介绍两个函数union(u，v)和find(p)的实现，并使用Leetcode 200提供更多详细信息。以岛屿数为例。

`find(p)` ， `union(u,v)`和优化 (`find(p)`, `union(u,v)`, and optimization)

There are two optimizations in the two functions: path compression and merge by rank.

这两个功能有两个优化：路径压缩和按等级合并。

`find(p)`和路径压缩 (`find(p)` and path compression)

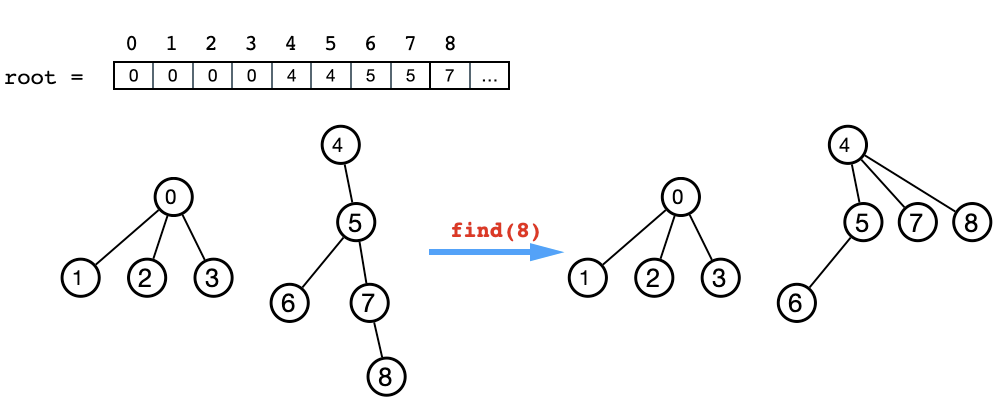
Given an element p, find(p) will return the representative of the set that p belongs to. Initially, we have an array root indicating the root of each element. Therefore, we can recursively or iteratively search for the root of p through root.

给定元素p ， find(p)将返回p所属集合的代表。最初，我们有一个数组root指示每个元素的根。因此，我们可以通过root递归或迭代地搜索p root 。

root=[0,0,0,0,4,4,5,5,7]
# recursively
def find(p):
    if root[p]!=p:
        return find(root[p])
    return p
# iteratively
def find(p):
    while root[p]!=p:
        p = root[p]
    return p

We can add path compression as optimization. While we are searching for the root of p, we can assign the root to the elements along the path. Also there will be two ways of implementing this.

我们可以添加路径压缩作为优化。在搜索p的根时，可以将根分配给路径上的元素。也将有两种方法来实现这一点。

# recursively
def find(p):
    if root[p]!=p:
        root[p] = find(root[p])
    return root[p]
# iteratively
def find(p):
    node = p
    while node!=root[node]:
        node = root[node]
    while p!=node:
        par = root[p]
        root[p] = node
        p = par
    return p

`union(u,v)`并按等级合并 (`union(u,v)` and merge by rank)

Given two elements u and v, union(u,v) merges the sets that u and vbelong to accordingly into one. To avoid the case shown below, we can add merge by rank as optimization.

给定两个元素u和v ， union(u,v)将u和v所属的集合相应地合并为一个。为了避免出现以下情况，我们可以添加按等级合并作为优化。

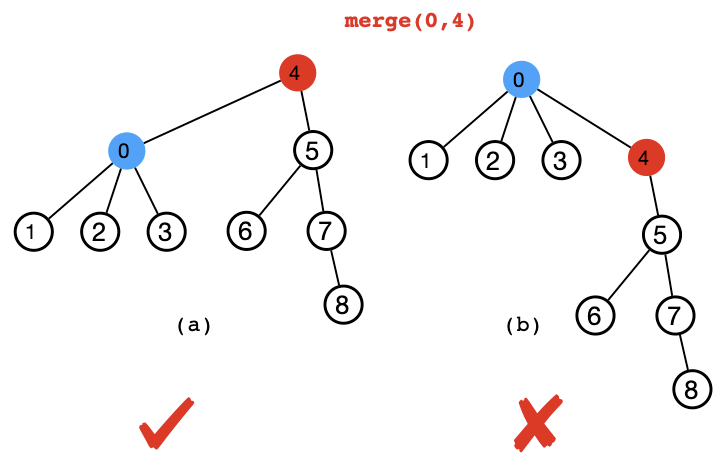
We can have an array rank indicating the height of each node and when we merge two sets, we would always seek to put the set with lower rank under the set with a higher rank.

我们可以有一个数组rank指示每个节点的高度，并且当我们合并两个集合时，我们总是试图将等级较低的集合放在等级较高的集合之下。

def union(u,v):
    u_root = find(u)
    v_root = find(v)
    if rank[u_root]>rank[v_root]:
        root[v_root] = u_root
    elif rank[u_root]<rank[v_root]:
        root[u_root] = v_root
    else:
        root[v_root] = u_root
        rank[u_root] += 1

复杂性 (Complexities)

Without path compression and merge by rank, the time complexity for find(p) could be O(n)O(n) and

如果没有路径压缩和按等级合并，则find(p)的时间复杂度可能为O(n) O ( n )和

Leetcode200。岛屿数(Leetcode 200. Number of Islands)

Initially, we would assign all '1' element as an isolated island. While we are iterating from top to bottom and from left to right, if we find its right neighbour or its neighbour below is also '1', we can conduct union(u,v). Remember to deduct 1 from the total number of the island when we merge two sets.

最初，我们将所有'1'元素分配为一个孤立的岛。当我们从上到下，从左到右进行迭代时，如果我们发现它的右邻居或下面的邻居也是'1' ，我们可以进行union(u,v) 。当我们合并两个集合时，请记住从岛的总数中减去1 。

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        if not grid or not grid[0]: return 0
        row,col = len(grid),len(grid[0])
        root = [i for i in range(row*col)]
        ranks = [0]*(row*col)
        cnt = 0
        for r in range(row):
            for c in range(col):
                # count each '1' as an isolated island
                if grid[r] == '1':
                    cnt += 1
        def find(p):
            # add path compression
            if root[p]!=p:
                root[p] = find(root[p])
            return root[p]
         
        def union(u,v):
            # add merge by rank
            nonlocal cnt
            u_root = find(u)
            v_root = find(v)
            if u_root == v_root: return
            if ranks[u_root] > ranks[v_root]: root[v_root] = u_root
            elif ranks[u_root] < ranks[v_root]: root[u_root] = v_root
            else:
                root[v_root] = u_root
                ranks[u_root] += 1
            # remember to deduct 1 from the total number of islands
            cnt -= 1
             
        for r in range(row):
            for c in range(col):
                if grid[r] == '0': continue
                # union connected '1's
                if r+1<row and grid[r+1] == '1': union(r*col+c,(r+1)*col+c)
                if c+1<col and grid[r] == '1': union(r*col+c,r*col+c+1)
        return cnt