动态表单设计与实现_通过动态编程实现更好的表单设计

动态表单设计与实现

Programming web forms is not usually associated with recursive algorithms or optimization techniques, but in this article we will show a problem that we faced, and how we managed to solve it with an efficient algorithm, by applying recursion and Dynamic Programming: building nice-looking forms!

Web表单编程通常不与递归算法或优化技术相关联，但是在本文中，我们将展示我们面临的问题，以及如何通过应用递归和动态编程来设法用有效的算法解决它：构建美观形式！

问题：建立一个好的表格 (The Problem: Building a nice form)

Let’s talk about the problem. The client needed to be able to produce multiple forms onscreen, with different sets of fields. Since the number of forms would be growing all the time, a “form creator” was desired: it would take a “form description” (basically, a list of fields in a specified order) as input and produce the right screen form as output. For example, the form fragment shown below could be produced by our system.

让我们谈谈这个问题。 客户需要能够在屏幕上生成具有不同字段集的多种表单。 由于表单的数量一直在增长，因此需要一个“表单创建者”：它将以“表单描述”(基本上是指定顺序的字段列表)作为输入，并生成正确的屏幕表单作为输出。 例如，下面显示的表单片段可以由我们的系统生成。

The goal for the algorithm: build a nice form like this, with properly justified fields

该算法的目标：构建一个具有适当对齐字段的类似形式的漂亮表单

However, there was a problem, an extra condition: the form had to “look nice”, applying justification to get even margins. But (there’s always a but) the widths of the fields were not necessarily such that all rows would be full, so you’d need to break rows and stretch fields to achieve the desired look.

但是，有一个问题，一个额外的条件：表格必须“看起来不错”，并应用对齐来获得均匀的边距。 但是(总是有一个but)字段的宽度并不一定要使所有行都填满，因此您需要断开行并拉伸字段才能获得所需的外观。

If you know about the internal details of the TEX typesetting system, you may be aware of the Knuth-Plass algorithm line-breaking algorithm that tackles the question of splitting paragraphs “nicely”. What we are doing here is at heart the same problem (in fact we could have based our logic on the mentioned algorithm) but we want to focus on the path to arrive at a valid algorithm.

如果您知道TEX排版系统的内部细节，您可能会知道Knuth-Plass算法的换行算法，可以很好地解决段落分割问题。 我们在这里所做的本质上是一个相同的问题(实际上，我们可以根据所提到的算法来建立逻辑)，但是我们希望专注于获得有效算法的路径。

To better understand the problem, let’s imagine we had five fields, with widths 7, 2, 5, 3, and 6 respectively, to be displayed in rows with a width of 10.

为了更好地理解问题，让我们假设我们有五个字段，分别以7、2、5、3和6的宽度显示在宽度为10的行中。

These are the five blocks we must fit in rows of width 10

这是我们必须适合宽度为10的行的五个块

How can we proceed? Some little experimentation shows that you cannot manage with fewer than 3 rows, and that 4 or more rows lead to too much wasted space. (Actually there won’t be “empty space” in the rows, since we won’t leave spaces around blocks, but rather make them wider to fit. In any case, we do have to know how much empty space will be left on each row, in order to then decide how to expand the blocks on it.)

我们该如何进行？ 一些小的实验表明，您管理的行数不能少于3行，并且4行或更多行会导致过多的空间浪费。 (实际上，行中不会有“空白空间”，因为我们不会在块周围留出空间，而是将它们扩大以适合放置。在任何情况下，我们都必须知道还剩下多少空白空间。每行，然后决定如何扩展其上的块。)

So, how can we fit these blocks in three rows? The first possibility would be applying a “greedy” algorithm: fit as many blocks in a row as possible, before moving to a new row. With this approach, we’d get the following layout.

那么，如何将这些块分成三排？ 第一种可能性是应用“贪婪”算法：在移至新行之前，在一行中尽可能多地容纳块。 通过这种方法，我们将获得以下布局。

A first layout for our blocks, produced by a “greedy” algorithm

由“贪婪”算法生成的块的第一个布局

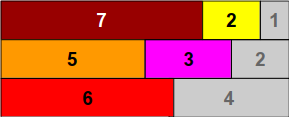
But this is not the only possibility! If we don’t include the 2-block in the first row, and move it to the next row instead, it leads to different alternatives. For example, we could totally fill the second row with the 2-, 5-, and 3-blocks, and get another layout.

但这不是唯一的可能性！ 如果我们不在第一行中包含2块，而是将其移至下一行，则会导致不同的选择。 例如，我们可以用2、5和3块完全填充第二行，并获得另一种布局。

An alternative second layout

另一种第二布局

And there’s one more layout: instead of filling the second row, we could move the 3-block to the last row, and this would be the result.

还有另一种布局：我们可以将3块移动到最后一行，而不是填充第二行，这就是结果。

A third possibility

第三种可能性

We can also look at solutions with 4 or 5 rows, but they require adding too much empty space — though we’ll qualify below what we mean by this.

我们也可以查看具有4或5行的解决方案，但是它们需要添加太多的空白空间-尽管我们的条件要低于此含义。

What’s the preferred solution — which one should be considered best? We need to establish a metric to decide which layout is to be considered the optimum one. We have to define a formula to calculate a row-wise cost, in terms of how many extra padding we added. Given the option, we prefer adding smaller spaces in many rows, than adding bigger spaces in few rows. So, let’s define the cost per row as the added space but squared, and the total cost will then be the sum of all the row costs.

首选的解决方案是什么-应该被认为是最好的解决方案？ 我们需要建立一种度量标准，以决定哪种布局被认为是最佳布局。 我们必须定义一个公式，根据添加的额外填充量来计算逐行成本。 给定该选项，我们宁愿在多行中添加较小的空间，而不是在几行中添加较大的空间。 因此，让我们将每行的成本定义为增加的空间但平方，然后总成本将是所有行成本的总和。

Why square the numbers? Imagine you had 2 spaces to add: if you add all of them in a single row, the cost would be 2²=4, but if you added 1 space to two lines, the cost would be just 1²+1²= 2. Squaring the numbers before adding them makes having many small numbers preferrable to having fewer larger ones. Obviously, squaring is not the only possible way to get numbers to behave the way we want (why not cubing? or exponentiating?) but it’s a simple solution that works well, so let’s use it.

为什么对数字求平方？ 假设您要添加2个空格：如果将所有空格都添加到一行中，则成本为2²= 4，但是如果您向两行添加1个空格，则成本仅为1²+1²= 2。在添加数字之前，使许多小数字比少一些大数字更可取。 显然，平方不是让数字表现出我们想要的方式(为什么不求积还是求幂？)的唯一可能方法，但是它是一个行之有效的简单解决方案，因此让我们使用它。

With this definition, the cost for the first layout would be 1²+2²+4²= 1+4+16= 21, the second cost would be 3²+0²+4²= 9+0+16= 25, and the third cost 3²+3²+1²= 9+9+1= 19. Thus, we’d consider the latter to be the one our algorithm should produce… but how do we code that? Let’s turn to this.

按照这种定义，第一个布局的成本为1²+2²+4²= 1 + 4 + 16 = 21，第二个成本为3²+0²+4²= 9 + 0 + 16 = 25，第三个成本为3² +3²+1²= 9 + 9 + 1 = 19.因此，我们认为后者是我们的算法应该产生的那种……但是我们如何编码呢？ 让我们转向这个。

解决方案：动态编程算法 (The Solution: a Dynamic Programming algorithm)

How can we solve find the appropriate row breaks for our form? A very obvious (and awful!) way to do is would be trying out all possible break points between blocks, and see which combination looks better — but the number of combinations to test grows exponentially with the number of blocks, so this approach is totally out of the question. We must do better!

我们如何解决找到适合我们表格的换行符？ 一种非常明显的方法(很糟糕！)是尝试使用块之间的所有可能的断点，并查看哪种组合看起来更好-但是要测试的组合的数量与块的数量成指数增长，所以这种方法是完全毫无疑问。 我们必须做得更好！

Assume we have a list of block widths; in our case, [7, 2, 5, 3, 6]. We also have a maximum width to achieve in each row: MW. Let’s think recursively: what’s the best way of distributing padding among the blocks? Let’s make it general: if we want to distribute a fragment of the blocks from position p to position q in an optimal way, we can use the logic below — and applying it with p pointing to the first block and q to the last block would solve our original problem.

假设我们有一个块宽度列表； 在我们的例子中是[7、2、5、3、6]。 在每一行中，我们还具有一个最大宽度： MW 。 让我们递归地思考：在块之间分配填充的最佳方法是什么？ 让我们概括地说：如果我们要以最佳方式分配从位置p到位置q的块片段，则可以使用下面的逻辑-将其应用于p指向第一个块，将q指向最后一个块将解决我们原来的问题。

1. sum the widths of all fields from p to q inclusive; call this sum s

   将所有字段的宽度相加，从p到q(含)； 把这个和S

2. if s is not greater than MW, the cost of this fragment is (MW-s)², and there’s nothing more to be done; we cannot do any better by splitting the fragment in two or more rows.

   如果s不大于MW ，则此片段的成本为( MW - s )²，且无更多操作可做； 我们无法通过将片段分成两行或更多行来做得更好。

3. if s exceeds MW, we need to add some row breaks… but where? The solution is recursive: try splitting the fragment in two pieces in all possible ways (the first piece would go from p to r, and the second from r+1 to q) and see which split produces the lowest cost; that’s your solution.

   如果s超过MW ，我们需要添加一些换行符...但是在哪里？ 解决方案是递归的：尝试以所有可能的方式将片段分成两部分(第一部分从p到r ，第二部分从r + 1到q )，看看哪个分割产生最低的成本； 那是您的解决方案。

Can we code this? Sure; in JavaScript, the following would do. (The code isn’t complete; for example, we’re neither recording what breaks we found, nor actually padding fields — let’s just focus on finding the best breaks, our main problem here.) Let’s assume we have a totalWidth(x,y) function that calculates the sum of the widths of blocks x through y.

我们可以编码吗？ 当然; 在JavaScript中，可以做到以下几点。 (代码不完整；例如，我们既没有记录发现的中断，也没有填充字段-我们只专注于找到最好的中断，这是我们的主要问题。)假设我们有一个totalWidth(x， y)函数，计算块x到y的宽度之和 。

const costOfFragment = (p, q) => {
  const s = totalWidth(p, q);  // fits in single row?
  if (s <= MW) return (MW - s) ** 2;  // no fit; try row breaks
  let opt = Infinity;
  for (let r = p; r < q; r++) {
    const try = costOfFragment(p, r) + costOfFragment(r + 1, q);
    if (try < c) opt = try;
  }
  return opt;
};

If the fields fit in a single row, we return the cost without any further do. Otherwise, we start trying out different row breaks using r, and we calculate the cost of a possible line break in try, by recursively calling costOfFragment. The best (lowest) achieved total is stored in opt.

如果这些字段适合一行，我们将不做任何进一步的处理就返回成本。 否则，我们将开始使用r尝试不同的行中断，并通过递归调用costOfFragment来计算try中可能发生的行中断的代价 。 达到的最佳(最低)总数存储在opt中 。

This logic works! Let’s see how we’d process our five blocks from above to make them fit in 10-width rows. Starting with the five blocks, we’d have to try four possible splits, since the blocks don’t fit in a single row.

这种逻辑有效！ 让我们看看如何处理上面的五个块，以使其适合10宽度的行。 从五个块开始，我们将不得不尝试四个可能的拆分，因为这些块无法容纳在一行中。

All possible ways to split our blocks in rows

所有可能的将行拆分为块的方法

The diagram above shows all the possible splits that would be attempted; let’s add the information about costs, to find what would be the best solution. Numbers in red are costs, calculated according to our squaring and summing definition.

上图显示了所有可能的分割尝试； 让我们添加有关成本的信息，以找到最佳解决方案。 红色数字是费用，是根据我们的平方和总和定义计算的。

Each split, with its associated cost; the total final cost would be 19

每次拆分及其相关成本； 最终总费用为19

Let’s recap the rules for costs:

让我们回顾一下费用规则：

• if you don’t have a split, to cost is the added space, squared: for instance, at the bottom left corner you have a single [5] which costs 25 (you need to add 5 spaces to get 10), a [3,6] which costs 1 (1 added space, squared), a [5,3] which costs 4 (2 added spaces, squared), and a [6] which costs 16 (4 added spaces, squared).
  如果您没有拆分，则成本为增加的空间(平方)：例如，在左下角，您有一个[5]，其成本为25(您需要添加5个空间才能得到10)， 3,6]花费1(1个增加的空间，平方)，[5,3]花费4(2个增加的空间，平方)，而[6]花费16(4个增加的空间，平方)。
• the total cost of a series of rows is just the sum of the individual splits — for example, if you split [5,3,6] in two rows with [5] and [3,6], the cost is 26 (25 from the 5 and 1 from the 3+6), and if you split it in [5,3] and [6], the cost is 20 (16 plus 4).
  一系列行的总成本只是各个拆分的总和-例如，如果将[5,3,6]分为[5]和[3,6]两行，则成本为26(25从5和1从3 + 6)，如果将其拆分为[5,3]和[6]，则成本为20(16加4)。
• if you have a split, the cost is the minimum cost of all the possible splits in rows. As an example, again near the bottom left corner, the cost for splitting [5,3,6] is 20, the minimum cost of its two possible splits, with individual costs of 26 and 20
  如果您有拆分，则成本是所有可能的拆分行中的最低成本。 例如，再次在左下角附近，分割[5,3,6]的成本为20，这是两次可能分割的最低成本，单个成本分别为26和20

Our logic produces the result we discussed above, and the optimum solution for our five blocks costs 19, and requires three lines: one with the 7-block alone, other with the 2- and 5-blocks, and the last with the 3- and 6-blocks. Great!

我们的逻辑产生了我们上面讨论的结果，五个块的最佳解决方案成本为19，并且需要三行：一个单独包含7个块，另一个包含2和5块，最后一个包含3个行和6块。 大！

But…

但…

通过动态编程进行优化 (Optimizing through Dynamic Programming)

There’s a problem with the process above… the algorithm is slow — mainly because it redoes several calculations over and over. The diagram below shows that; each colored block is calculated more than once.

上面的过程有一个问题……算法很慢-主要是因为它一遍又一遍地重做了一些计算。 下图显示了这一点； 每个彩色块的计算均不止一次。

All colored splits were calculated twice or more — unefficient!

所有彩色分割均计算两次或更多次-效率低下！

We can do better, by applying Dynamic Programming: a technique to solve a complex problem by breaking it down into simpler versions of the same problem, whose solutions are stored somewhere, to avoid having to re-do calculations.

通过应用动态编程 ，我们可以做得更好：通过将复杂的问题分解为相同问题的更简单版本来解决复杂问题的技术，该解决方案的解决方案存储在某个地方，而无需重新进行计算。

In our case, how can we skip repeating calls? We could obviously create and update a cache of results by hand, but we don’t need to do so, because this is a problem that we already know how to solve: memoizing! Basically, if you take a function and memoize it, you get a new one that behaves identically, except that it will cache calculated results; if you call the memoized function with parameters that you had already passed before, it won’t do any calculations and return the value from the cache instead.

在我们的情况下，如何跳过重复通话？ 显然，我们可以手工创建和更新结果缓存，但是我们不需要这样做，因为这是我们已经知道如何解决的问题： 记忆 ！ 基本上，如果您使用一个函数并将其记忆化，则您会得到一个行为相同的新函数，只是它将缓存计算的结果。 如果您使用之前已经传递过的参数来调用备忘录的函数，则它将不进行任何计算，而是从缓存中返回该值。

We already saw another usage of memoizing to optimize API calls; check my Memoize JavaScript Promises for Performance article for that. We developed a memoizing function of our own there, but you can also opt for the very efficient fast-memoize library instead, among other possibilities.

我们已经看到了备忘录的另一种用法，以优化API调用。 请查看我的“ 为性能记住Memoize JavaScript Promise”一文。 我们在那里开发了自己的记忆功能，但是您还可以选择非常高效的快速记忆库。

How much work would we avoid? The diagram below shows the enhanced results: all grey blocks need no recalculation, and in particular the arrows point to places where no recursion was even needed, because the work had already been done.

我们将避免多少工作？ 下图显示了增强的结果：所有灰色块都无需重新计算，尤其是箭头指向甚至不需要递归的位置，因为该工作已经完成。

The Dynamic Programming solution avoids recalculating the blocks in grey

动态编程解决方案避免了重新计算灰色块

In the diagram above, blocks in grey are those that do not need to be recomputed, because the necessary work was already done before and saved. If you compare this figure with the previous ones, you’ll notice that two parts of the diagram (where the green arrows are) do not appear any longer — those are calls that were not needed because of the caching.

在上图中，灰色块是不需要重新计算的块，因为之前已经完成了必要的工作并保存了它们。 如果将该图与之前的图进行比较，您会注意到该图的两个部分(绿色箭头所在的位置)不再出现​​-这些是由于缓存而不需要的调用。

In terms of coding, the change is minimal.

在编码方面，变化很小。

const costOfFragment = memoize((p: number, q: number) => {
  .
  . no changes here!
  .
});

That does it! The optimized algorithm does minimal work, and finds a nice split quickly.

做到了！ 经过优化的算法所做的工作最少，并且可以快速找到合适的分割。

摘要 (Summary)

We described an actual problem derived from a client’s request, and how we managed to solve it in an optimized way by applying Dynamic Programming and memoization, to go from a correct-but-slow algorithm to an also-correct-but-fast one, with minimal changes. This same techniques can be applied in many other contexts, for equally good performance enhancements; an all around win!

我们描述了一个来自客户请求的实际问题，以及我们如何通过应用动态编程和备注来以一种优化的方式设法解决该问题，从而从正确但缓慢的算法转变为又正确但快速的算法，变化最小。 相同的技术可以应用在许多其他情况下，以实现同样良好的性能增强。 全方位获胜！

翻译自: https://medium.com/globant/better-form-design-through-dynamic-programming-4287857056f4

动态表单设计与实现