t-sne 流形
Principal Component Analysis is a powerful method, but it often fails in that it assumes that the data can be modelled linearly. PCA expressed new features as linear combinations of existing ones by multiplying each by a coefficient. To address the limitations of PCA, various techniques have been created by apply for data with different specific structures. Manifold learning, however, seeks to find a method that can generalize to all structures of data.
主成分分析是一种强大的方法,但是它经常失败,因为它假定可以线性建模数据。 PCA通过将每个特征乘以一个系数,将新特征表示为现有特征的线性组合。 为了解决PCA的局限性,通过应用具有不同特定结构的数据已创建了各种技术。 但是,流形学习试图找到一种可以推广到所有数据结构的方法。
Different structures of data refer to its different attributes within the data. For instance, it may be linearly separable, or it may be very sparse. Relationships within the data may be tangent, parallel, enveloping, or orthogonal to others. PCA works well on a very specific subset of data structures, since it operates on the assumption of linearity.
数据的不同结构引用数据中其不同的属性。 例如,它可能是线性可分离的,或者可能非常稀疏。 数据内的关系可以是相切的,平行的,包络的或正交的。 PCA在非常具体的数据结构子集上运行良好,因为它在线性假设下运行。
To put things in context, consider 300 by 300 pixel headshots. Under perfect conditions, each of the images would be centered perfectly, but in reality, there are many additional degrees of freedom to consider, such as lighting or the tilt of the face. If we were to treat a headshot as a point in 90,000 dimensional space, changing various effects like tilting the head or looking in a different direction move it nonlinearly through space, even though it is the same object with the same class.
为了说明问题,请考虑300 x 300像素的爆头。 在理想条件下,每个图像都将完美居中,但实际上,要考虑许多其他自由度,例如光照或面部倾斜。 如果我们将爆头视为90,000维空间中的一个点,则改变它的各种效果(例如倾斜头部或朝不同的方向看),即使它是同一类别的同一对象,也会在空间中非线性地移动它。
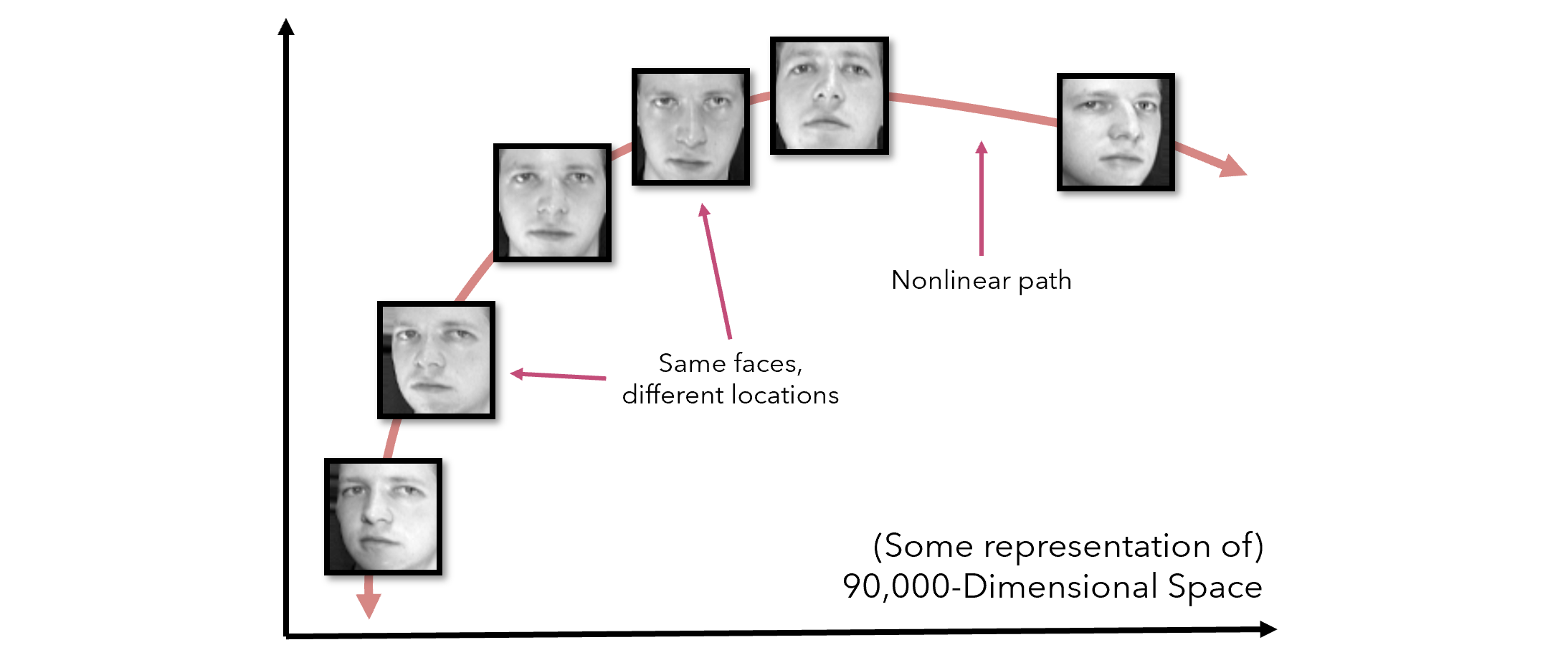
This kind of data appears very often in real-world datasets. In addition to this effect, PCA is flustered when presented with skewed distributions, extreme values, and multiple dummy (one-hot encoded) variables (see Nonlinear PCA for a solution to this). There is a need for a generalizable method of dimensionality reduction.
这种数据经常出现在现实数据集中。 除此效果外,当PCA出现偏斜的分布,极值和多个虚拟(一次热编码)变量时,也会感到不安(有关此问题的解决方案,请参阅非线性PCA )。 需要一种通用的降维方法。
Manifold learning refers to this very task. There are many approaches within manifold learning that perhaps have been seen before, such as t-SNE and Locally Linear Embeddings (LLE). There are many articles and papers that go into the technical and mathematical details of these algorithms, but this one will focus on the general intuition and implementation.
流形学习就是指这项任务。 在流形学习中可能已经见过许多方法,例如t-SNE和局部线性嵌入(LLE)。 关于这些算法的技术和数学细节,有很多文章和论文,但是这一文章将重点介绍一般的直觉和实现。
Note that while there have been a few variants of dimensionality reduction that are supervised (e.g. Linear/Quadratic Discriminant Analysis), manifold learning generally refers to an unsupervised reduction, where the class is not presented to the algorithm (but may exist).
请注意,虽然有一些降维的变体是受监督的(例如, 线性/二次判别分析 ),但流形学习通常是指无监督的降维,其中该类未提供给算法(但可能存在)。
Whereas PCA attempts to create several linear hyperplanes to represent dimensions, much like multiple regression constructs as an estimation of the data, manifold learning attempts to learn manifolds, which are smooth, curved surfaces within the multidimensional space. As in the image below, these are often formed by subtle transformations on an image that would otherwise fool PCA.
PCA尝试创建几个线性超平面来表示维,就像使用多个回归构造作为数据估计一样,而流形学习则尝试学习流形,这些流形是多维空间内的光滑曲面。 如下图所示,这些通常是通过对图像进行微妙的转换而形成的,否则将使PCA蒙蔽。
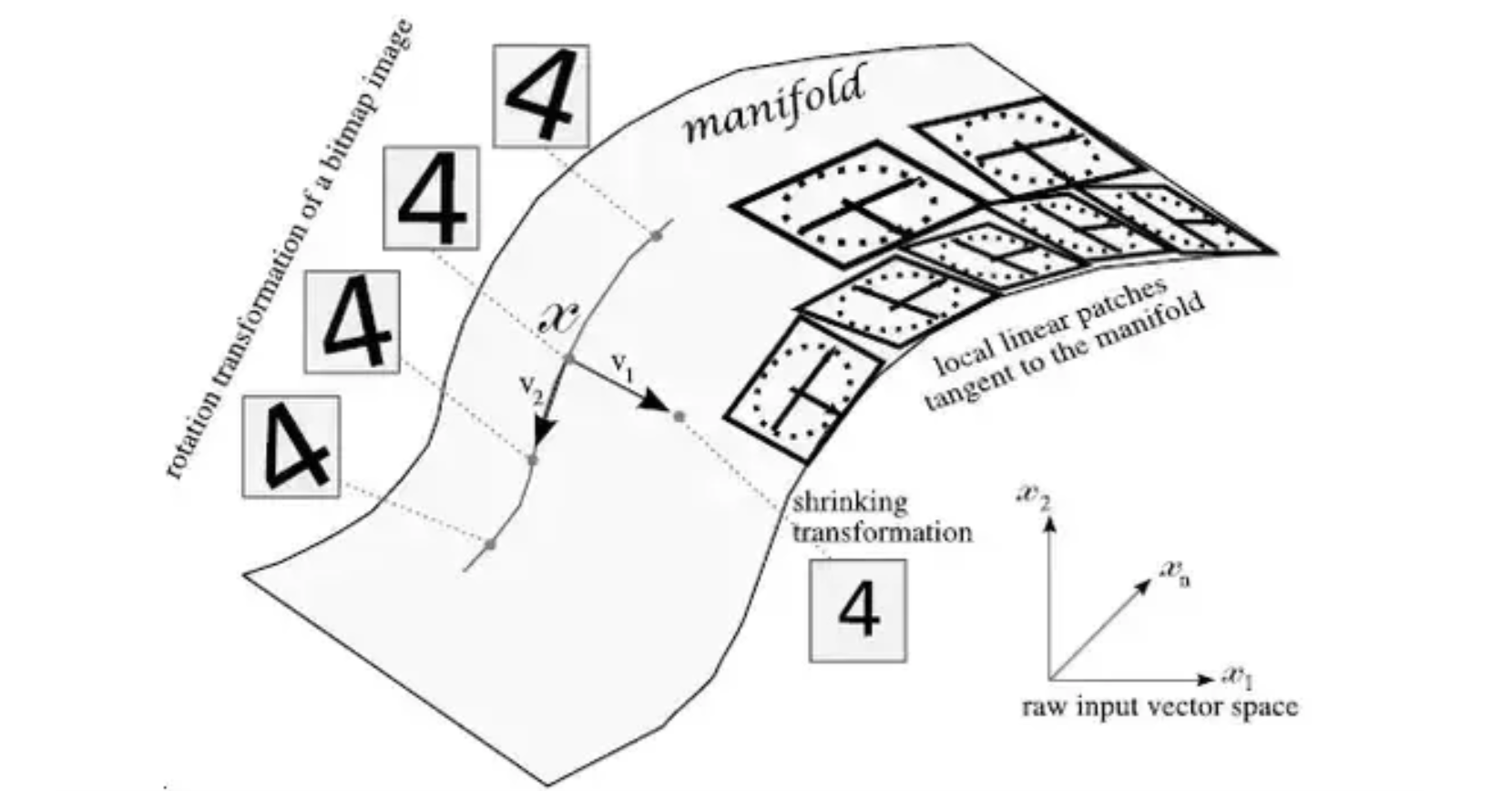
Then, ‘local linear patches’ that are tangent to the manifold can be extracted. These patches are usually in enough abundance such that they can accurately represent the manifold. Because these manifolds are not modelled by any one mathematical function but by several small linear patches, these linear neighborhoods can model any manifold. Although this may not be explicitly how certain algorithms approach the modelling of manifolds, the fundamental ideas are very similar.
然后,可以提取与歧管相切的“局部线性面片”。 这些补丁通常足够丰富,因此它们可以准确地代表歧管。 由于这些歧管不是通过任何一个数学函数而是通过几个小的线性斑块来建模的,因此这些线性邻域可以对任何歧管进行建模。 尽管这可能不是某些算法如何明确歧管建模的明确方法,但基本思想非常相似。
The following are fundamental assumptions or aspects of manifold learning algorithms:
以下是流形学习算法的基本假设或方面:
- There exist nonlinear relationships in the data that can be modelled through manifolds — surfaces that span multiple dimensions, are smooth, and not too ‘wiggly’ (too complex). The manifolds are continuous. 数据中存在可以通过流形建模的非线性关系-跨多个维度的表面,光滑且不太“摇摆”(太复杂)。 歧管是连续的。
- It is not important to maintain the multi-dimensional shape of data. Instead of ‘flattening’ or ‘projecting’ it (as with PCA) with specific directions to maintain the general shape of the data, it is alright to perform more complex manipulations like unfolding a coiled strip or flipping a sphere inside out. 保持数据的多维形状并不重要。 可以使用特定的方向来“展平”或“投影”该数据(如PCA)以保持数据的总体形状,而可以执行更复杂的操作,例如展开卷状条带或将球体向内翻转。
- The best method to model manifolds is to treat the curved surface as being composed of several neighborhoods. If each data point manages to preserve the distance not with all the other points but only the ones close to it, the geometric relationships can be maintained in the data. 对歧管建模的最佳方法是将曲面视为由多个邻域组成。 如果每个数据点都设法与其他点保持距离而不是与其他点保持距离,则可以在数据中保留几何关系。
This idea can be understood well by looking at different approaches between unravelling this coiled dataset. On the left is a more PCA-like approach towards preserving the shape of the data, where each point is connected to each other. On the right, however, is an approach in which only the distance between neighborhoods of data points are valued.
通过研究拆解该线圈数据集之间的不同方法,可以很好地理解此想法。 左侧是一种更类似于PCA的方法来保持数据的形状,其中每个点都相互连接。 但是,右侧是一种方法,其中仅评估数据点邻域之间的距离。
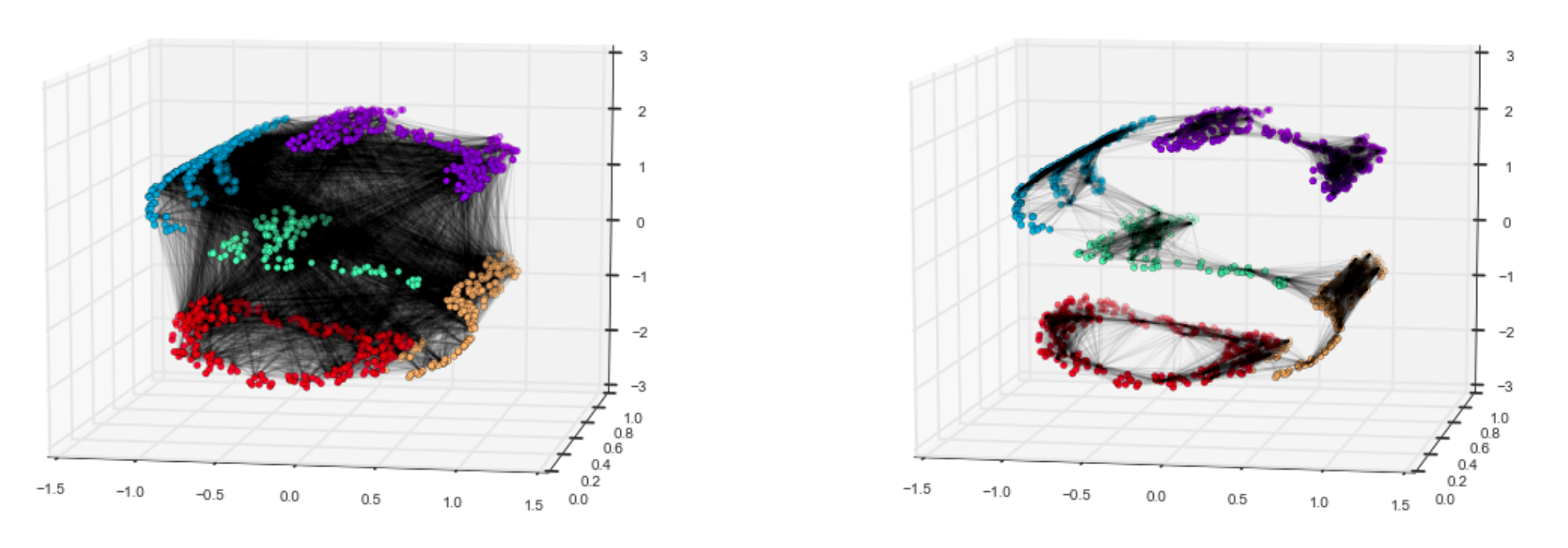
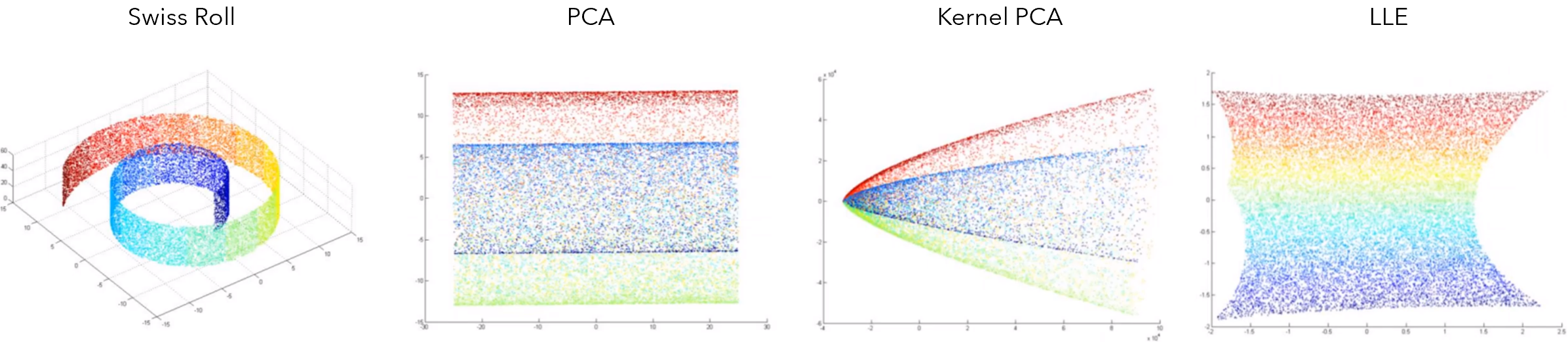
This relative disregard for points outside of a neighborhood leads to interesting results. For instance, consider this Swiss Roll dataset, which was coiled in three dimensions and reduced to a strip in two dimensions. In some scenarios, this effect would not be desirable. However, if this curve was the result of, say, tilting of the camera in an image or external effects on audio quality, manifold learning does us a huge favor by delicately unravelling these complex nonlinear relationships.
相对不考虑邻域外的点会产生有趣的结果。 例如,考虑此Swiss Roll数据集,该数据集在三个维度中盘绕,在二维中简化为带状。 在某些情况下,这种效果是不希望的。 但是,如果这条曲线是由于摄像机在图像中倾斜或外部效果对音频质量的影响而导致的,那么通过精细地解开这些复杂的非线性关系,多种学习方法将为我们提供巨大的帮助。
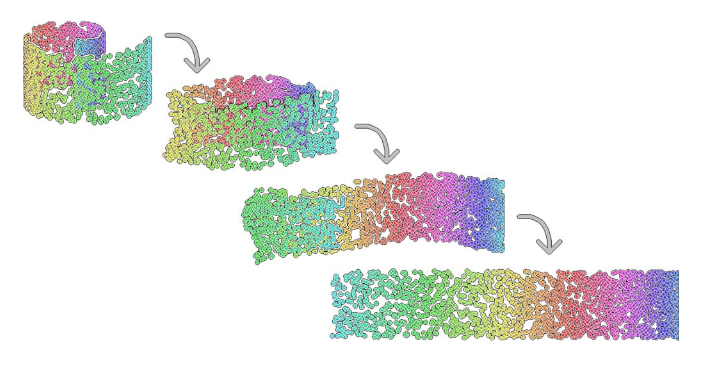
On the Swiss Roll dataset, PCA and even specialized variations like Kernel PCA fail to capture the gradient of values. Locally Linear Embeddings (LLE), a manifold learning algorithm, on the other hand, is able to.
在Swiss Roll数据集上,PCA甚至专用变体(如内核PCA)都无法捕获值的梯度。 另一方面,局部线性嵌入(LLE)是一种流形学习算法。
Let’s get into more detail about three popular manifold learning algorithms: IsoMap, Locally Linear Embeddings, and t-SNE.
让我们更详细地了解三种流行的流形学习算法:IsoMap,局部线性嵌入和t-SNE。
One of the first explorations in manifold learning was the Isomap algorithm, short for Isometric Mapping. Isomap seeks a lower-dimensional representation that maintains ‘geodesic distances’ between the points. A geodesic distance is a generalization of distance for curved surfaces. Hence, instead of measuring distance in pure Euclidean distance with the Pythagorean theorem-derived distance formula, Isomap optimizes distances along a discovered manifold.
流形学习的最早探索之一是Isomap算法,它是Isometric Mapping的缩写。 Isomap寻求一个维数较低的表示形式,以保持点之间的“大地距离”。 测地距离是曲面距离的概括。 因此,Isomap不会使用勾股定理衍生的距离公式来测量纯欧几里得距离中的距离,而是会优化沿着发现的流形的距离。
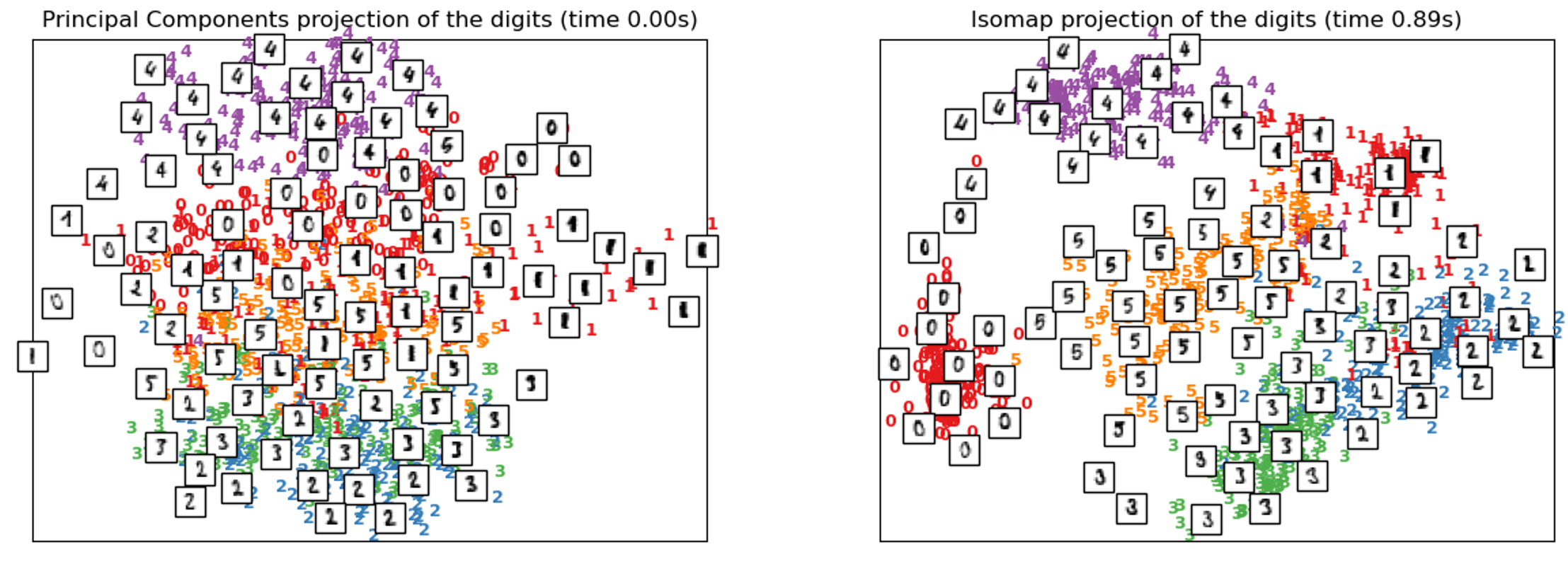
Isomap performs better than PCA when trained on the MNIST dataset, showing a proper sectioning-off of different types of digits. The proximity and distance between certain groups of digits is revealing to the structure of the data. For instance, the ‘5’ and the ‘3’ that are close to each other (in the bottom left) in distance indeed look similar.
在MNIST数据集上进行训练时,Isomap的性能优于PCA,显示了对不同类型数字的正确分割。 某些数字组之间的接近度和距离正在揭示数据的结构。 例如,距离(在左下角)彼此接近的“ 5”和“ 3”的确看起来相似。
Below is the implementation of Isomap in Python. Since MNIST is a very large dataset, you may want to only train Isomap on the first 100 training examples with .fit_transform(X[:100]).
以下是Python中Isomap的实现。 由于MNIST是一个非常大的数据集,因此您可能只想使用.fit_transform(X[:100])在前100个训练示例中训练Isomap。
Locally Linear Embeddings use a variety of tangent linear patches (as demonstrated with the diagram above) to model a manifold. It can be thought of as performing a PCA on each of these neighborhoods locally, producing a linear hyperplane, then comparing the results globally to find the best nonlinear embedding. The goal of LLE is to ‘unroll’ or ‘unpack’ in distorted fashion the structure of the data, so often LLE will tend to have a high density in the center with extending rays.
局部线性嵌入使用各种切线线性面片(如上图所示)为流形建模。 可以考虑在本地对这些邻域中的每个邻域执行PCA,生成线性超平面,然后全局比较结果以找到最佳的非线性嵌入。 LLE的目标是以扭曲的方式“展开”或“解包”数据的结构,因此,LLE通常会在中心处具有较高的密度,且光线会延伸。
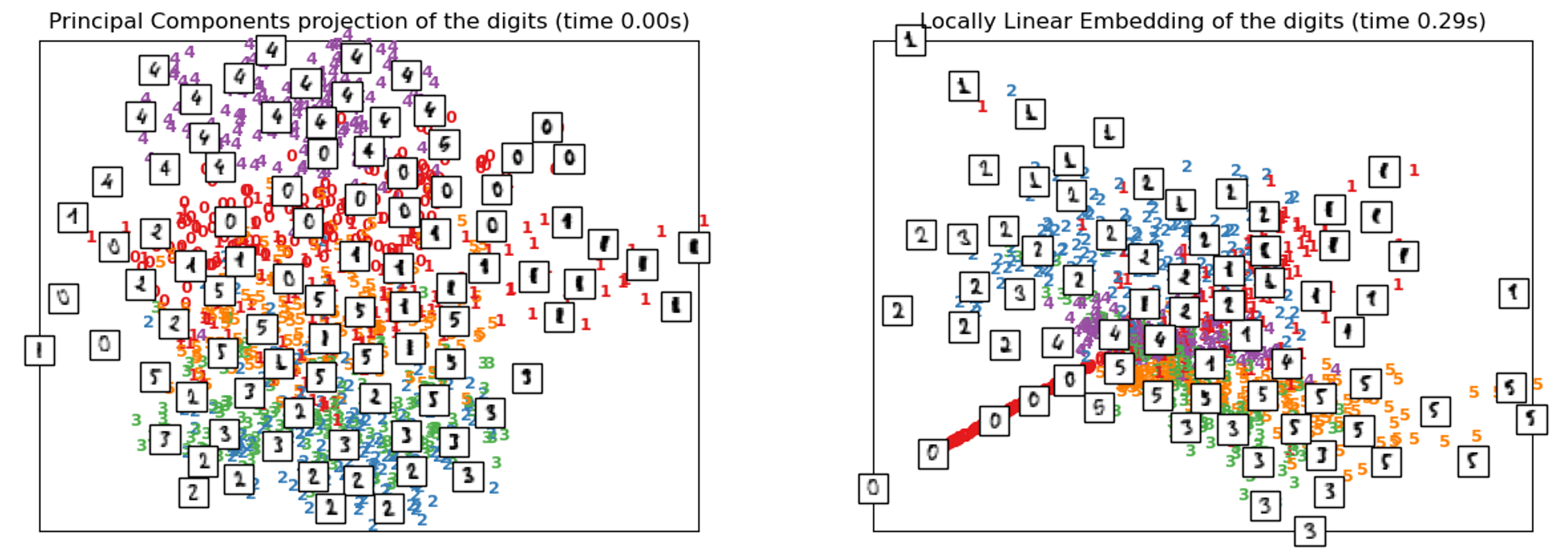
Note that LLE’s performance on the MNIST dataset is relatively poor. This is likely because the MNIST dataset consists of multiple manifolds, whereas LLE is designed to work on simpler datasets (like the Swiss Roll). It performs relatively similarly, or even worse, than PCA in this case. This makes sense; its ‘represent one function as several small linear ones’ strategy likely does not work well with large and complex dataset structures.
请注意,LLE在MNIST数据集上的性能相对较差。 这可能是因为MNIST数据集由多个流形组成,而LLE被设计为可用于更简单的数据集(如Swiss Roll)。 在这种情况下,它的性能与PCA相对相似,甚至更差。 这很有道理; 它的“将一个函数表示为几个小的线性函数”策略可能不适用于大型和复杂的数据集结构。
The implementation for LLE is as follows, assuming the dataset (X) has already been loaded.
假设数据集( X )已经加载,则LLE的实现如下。
t-SNE is one of the most popular choices for high-dimensional visualization, and stands for t-distributed Stochastic Neighbor Embeddings. The algorithm converts relationships in original space into t-distributions, or normal distributions with small sample sizes and relatively unknown standard deviations. This makes t-SNE very sensitive to the local structure, a common theme in manifold learning. It is considered to be the go-to visualization method because of many advantages it possesses:
t-SNE是高维可视化的最受欢迎选择之一,它代表t分布的随机邻居嵌入。 该算法将原始空间中的关系转换为t分布或样本量较小且标准偏差相对未知的正态分布。 这使得t-SNE对局部结构非常敏感,这是流形学习中的常见主题。 由于它具有许多优点,因此被认为是首选的可视化方法:
- It is able to reveal the structure of the data at many scales. 它能够以多种规模揭示数据的结构。
- It reveals data that lies in multiple manifolds and clusters 它揭示了位于多个流形和集群中的数据
- Has a smaller tendency to cluster points at the center. 将点聚集在中心的趋势较小。
Isomap and LLE are best use to unfold a single, continuous, low-dimensional manifold. On the other hand, t-SNE focuses on the local structure of the data and attempts to ‘extract’ clustered local groups instead of trying to ‘unroll’ or ‘unfold’ it. This gives t-SNE an upper hand in detangling high-dimensional data with multiple manifolds. It is trained using gradient descent and tries to minimize entropy between distributions. In this sense, it is almost like a simplified, unsupervised neural network.
最好使用Isomap和LLE来展开单个连续的低维流形。 另一方面,t-SNE专注于数据的本地结构,并尝试“提取”集群的本地组,而不是尝试“展开”或“展开”数据。 这使t-SNE在使用多个流形对高维数据进行纠缠方面具有优势。 它使用梯度下降进行训练,并试图使分布之间的熵最小。 从这个意义上讲,它几乎就像一个简化的,无监督的神经网络。
t-SNE is very powerful because of this ‘clustering’ vs. ‘unrolling’ approach to manifold learning. With a high-dimensional and multiple-manifold dataset like MNIST, where rotations and shifts cause nonlinear relationships, t-SNE performs even better than LDA, which was given the labels.
t-SNE非常强大,因为这种“聚类”与“展开”方法可以进行多种学习。 对于MNIST这样的高维和多流形数据集,其中的旋转和移动会导致非线性关系,因此t-SNE的性能甚至优于被赋予标签的LDA 。
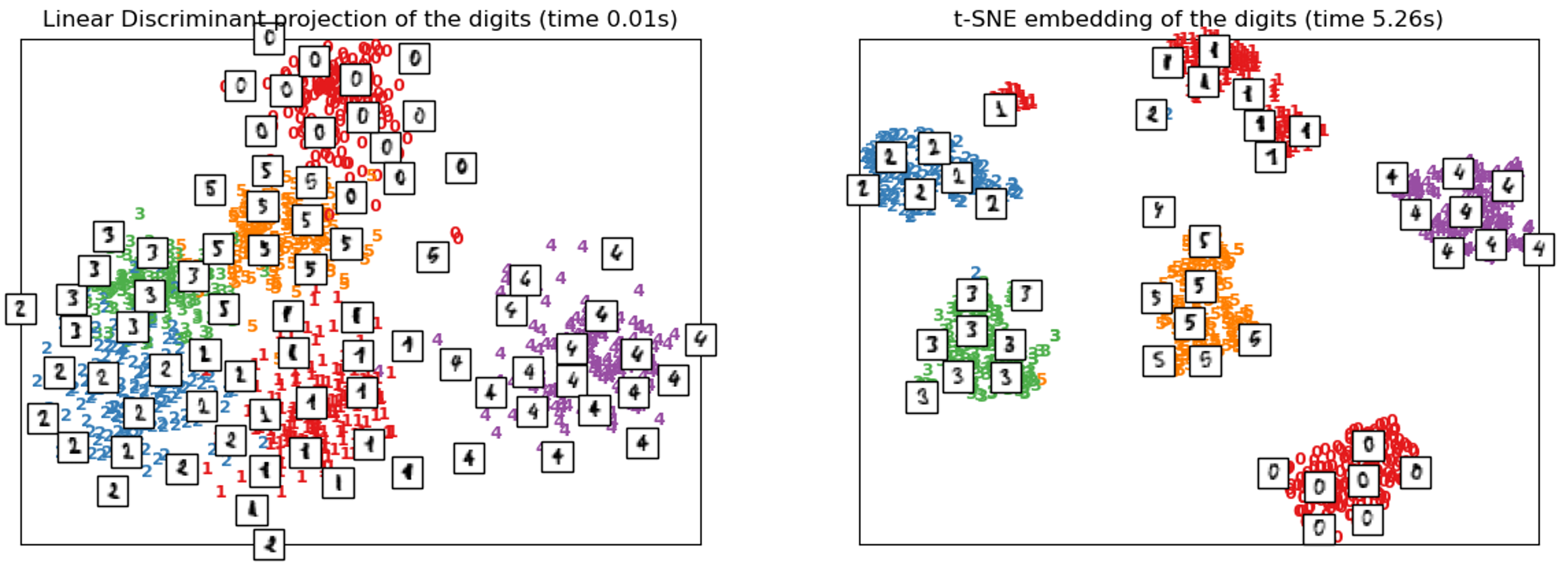
However, t-SNE does have some disadvantages:
但是,t-SNE确实有一些缺点:
- t-SNE is very computationally expensive (compare the runtimes in the diagrams above). It can take several hours on a million-sample dataset, whereas PCA can finish in seconds or minutes. t-SNE在计算上非常昂贵(请比较上图中的运行时)。 一百万个样本的数据集可能要花费几个小时,而PCA可以在几秒钟或几分钟内完成。
- The algorithm relies on randomness (stochastic) to pick seeds to construct embeddings, which can increase its runtime and decrease performance if the seeds happen to be placed poorly. 该算法依赖于随机性(随机性)来挑选种子来构建嵌入,如果种子恰好放置不当,则会增加其运行时间并降低性能。
- The global structure is not explicitly preserved (i.e. more emphasis on clustering than demonstrating global structures). However, in sklearn’s implementation this problem can be solved by initializing points with PCA, which is built especially to preserve the global structure. 没有明确保留全局结构(即,比起展示全局结构,更强调聚类)。 但是,在sklearn的实现中,可以通过使用PCA初始化点来解决此问题,而PCA专门为保留全局结构而构建。
t-SNE can implemented in sklearn as well:
t-SNE也可以在sklearn中实现:
Laurens van der Maaten, t-SNE’s author, says to consider the following when t-SNE yields a poor output:
t-SNE的作者Laurens van der Maaten说,当t-SNE的产出不佳时,请考虑以下几点:
As a sanity check, try running PCA on your data to reduce it to two dimensions. If this also gives bad results, then maybe there is not very much nice structure in your data in the first place. If PCA works well but t-SNE doesn’t, I am fairly sure you did something wrong.
作为健全性检查,请尝试对数据运行PCA,以将其缩减为两个维度。 如果这还会带来不好的结果,则可能一开始数据中可能没有很好的结构。 如果PCA运作良好,但t-SNE却不能,我很确定您做错了什么。
Why does he say so? As an additional reminder to hit the point home, manifold learning is not another variation of PCA but a generalization. Something that performs well in PCA is almost guaranteed to perform well in t-SNE or another manifold learning technique, since they are generalizations.
他为什么这么说? 作为进一步提醒您,综合学习不是PCA的另一种变化,而是一种概括。 在PCA中表现良好的事物几乎可以保证在t-SNE或其他多种学习技术中表现良好,因为它们是概括。
Much like an object that is an apple is also a fruit (a generalization), usually something is wrong if something does not yield a similar result as its generalization. On the other hand, if both methods fail, the data is probably inherently tricky to model.
就像是苹果的对象也是水果(概括)一样,如果某些事物不能产生与概括相似的结果,则通常是错误的。 另一方面,如果两种方法均失败,则数据可能固有地难以建模。
关键点 (Key Points)
- PCA fails to model nonlinear relationships because it is linear. PCA无法建模非线性关系,因为它是线性的。
- Nonlinear relationships appear in datasets often because external forces like lighting or the tilt can move a data point of the same class nonlinearly through Euclidean space. 非线性关系经常出现在数据集中是因为诸如光照或倾斜之类的外力可以使同一类的数据点在欧氏空间中非线性移动。
- Manifold learning attempts to generalize PCA to perform dimensionality reduction on all sorts of dataset structures, with the main idea that manifolds, or curved, continuous surfaces, should be modelled by preserving and prioritizing local over global distance. 流形学习试图推广PCA,以对所有类型的数据集结构执行降维,其主要思想是,应通过保留和优先考虑局部而不是全局距离来对流形或弯曲连续表面进行建模。
- Isomap tries to preserve geodesic distance, or distance measured not in Euclidean space but on the curved surface of the manifold. Isomap尝试保留测地线距离,即不是在欧几里得空间中而是在歧管的曲面上测量的距离。
- Locally Linear Embeddings can be thought of as representing the manifold as several linear patches, in which PCA is performed on. 可以认为局部线性嵌入将流形表示为几个线性面片,在其中进行PCA。
- t-SNE takes more of an ‘extract’ approach opposed to an ‘unrolling’ approach, but still, like other manifold learning algorithms, prioritizes the preservation of local distances by using probability and t-distributions. t-SNE采取了更多的“提取”方法,而不是“展开”方法,但是仍然像其他流形学习算法一样,通过使用概率和t分布来优先保留本地距离。
其他技术读物 (Additional Technical Reading)
Thanks for reading!
谢谢阅读!
翻译自: https://towardsdatascience.com/manifold-learning-t-sne-lle-isomap-made-easy-42cfd61f5183
t-sne 流形




















 3033
3033











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








