本文介绍了克莱姆法则在解线性方程组中的应用，特别是对于n*n线性方程组有唯一解的情况。讨论了在矩阵行列式计算量大时，如何利用Mathlab软件进行高效求解，强调理解原理的重要性，并探讨了行列式在数学中的美学价值。
地点：学院大自习室；人物：小刚，小慧，小明。
讨论内容：克拉姆法则与用Matlab软件求行列式。
7.1 克拉姆法则
我：“通过前两节的学习，我们算是彻底掌握了n阶行列式的计算，为什么要计算行列式？要不忘初心。其实我们一开始就是想解线性方程组，二、三元线性方程组可以用行列式方法平求解！四元或四元以上的线性方程组到底能不能用行列式来解呢？当时我们曾举过一个非常简单的例子，下面再举一个来验证一下二、三元线性方程组的解法可否移植到四元线性方程组上。”
小明：“我来验证一下。”
克莱姆在解线性方程组方面做出巨大贡献，克莱姆(Cramer,Gabriel，瑞士数学家 1704-1752)，1734年成为几何学教授，1750年任哲学教授。第一次正式引入坐标系的纵轴(Y轴)，然后讨论曲线变换，为了确定经过5个点的一般二次曲线的系数，应用了著名的“克莱姆法则”，即由线性方程组的系数确定方程组解的表达式。
7.2 数学软件Matlab
讨论到这里，我们三人都非常的开心，感觉自己学到了很多知识，可以用来解决以后遇到实际问题。可是过了一会，小慧提出了一个问题：
“如果有一个线性方程组模型，它的系数都很大，计算太麻烦，碰到这样的问题我只能知难而退！”
我：“提的好，李老师在课堂上对这个问题有交待。”
克莱姆法则应用于未知数个数与方程个数相等的n*n 的线性方程组，且系数行列式不能为零，即有唯一解的情况．当n较大时计算量通常很大。因此克莱姆法则的主要意义是在理论上，它明确指出了方程组的解与系数之间的关系．几个世纪前人们生活简单，线性方程组规模不大，行列式在解析几何和其它数学分支中起着重要作用。
目前在实际解线性方程组时手动计算的时代已经过去了，下面给大家介绍一个计算行列式的密秘武器：数学软件Matlab。
Matlab的使用
首先下载安装matlab7.0,安装完毕后打开程序，界面如下
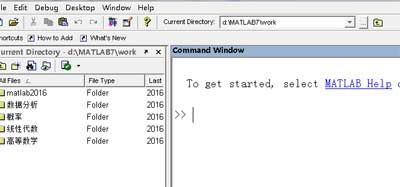
在matlab使用环境中有个Command Window窗口，在命令提示符>>光标处输入命令后，再回车键即可执行命令。
我：“李老师也说，虽然Matlab数学软件把我们从繁重的计算任务中解脱出来，但是对于行列式的计算原理我们必须得懂，就是虽然我们不手动算了，但是方法要会。”
小慧：“嗯，线性方程组不但有n*n，还有 m*n的情况，解也不并只有唯有解，如果有无穷多解，解应如何求？”
“显然行列式不能回答这些问题，所以我们必须引入新的工具来解决这些问题。”
我：“行列式学完了，我觉得行列式很美，你们想一想它的排列规律、它的计算，所以说数学是大自然的语言这话没错，人类与自然的交流是一个永恒的话题。人类从自然中索取物质，维持生命，同时又从它身上感悟美感，培养审美能力。大自然为什么给人类以美感呢？因为它蕴含有许多美的要素，如对称、和谐、奇巧、虚实、变化、新鲜等等。这些要素在我们人类的精神产品中，如数学、小说、戏剧、绘画、音乐中都可以找到，但只有在数学中才会体现得那么淋漓尽致，尤其是在对称、简洁和变化上。
小慧：“说的好啊，数学是人类智慧的结晶，只有数学才真正体现人之区别于动物的聪明之处，一张纸、一只笔就可以得到那么多美妙的结论，公理(事实)加上人脑的逻辑和推理使数学无往而不胜！”
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
