vecm模型怎么写系数_六角蜂窝格子紧束缚模型的计算

最近做过六角蜂窝格子（honeycomb lattice）上的一些紧束缚（tight-binding, TB）模型，以前上学时算石墨烯没弄明白的几个问题也大概弄懂了，在这里分享一下。大致分为四个部分：

1. 首先是honeycomb lattice傅里叶变换（FT）的两种规范，其中一种更简单，得到的TB哈密顿量也满足布里渊区的平移不变性。
2. 介绍一下什么是honeycomb lattice对应的“砖块格子”（brick lattice）。对不熟悉的人来说六角格子还是有点复杂，但其实可以将其拉成等价的像砖块一样的方格子，看起来更简单。
3. 介绍一下honeycomb lattice取开放边界时三种不同取法，以及对应的不同形态的边界态。
4. 介绍怎么计算开边界的厚板（slab）模型。可以直接写出N层的slab哈密顿量来对角化，或者用表面格林函数方法严格解。

1. Honeycomb lattice 傅里叶变换的两种规范

Honeycomb lattice有A，B两套子格子，每套格子内部有平移不变性。这也就是说每个原胞内有A，B两个site（图中蓝框里是一个原胞）。设原胞内AB距离为a，选取原胞基矢为

，对应的倒空间基矢为

。

Honeycomb lattice的晶格和布里渊区示意图

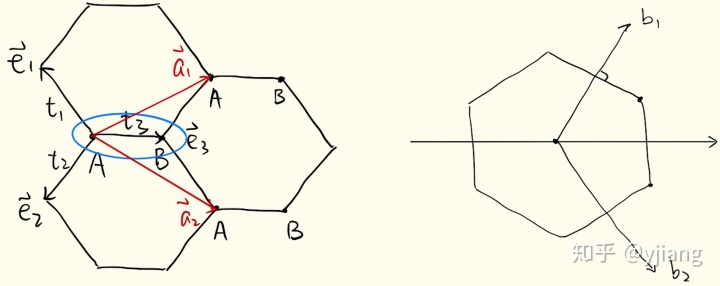
只考虑最近邻跃迁时，

。以图中A点为例，有三个最近邻B点，平移矢量分别为

。于是，

第一种FT规范：

FT的变换因子

就是格点A或者B的坐标。

第二种FT规范：

其中B的FT变换因子里多了一项

，是A到B的平移矢量。B的坐标减去

就是同一原胞内A的坐标。也就是说，在这种规范下，只把原胞的位置（即A的位置）作为FT的变换因子，忽略原胞内部细节，将B视为与A处于同一位置。这相当于做了规范变换

，不影响物理可观测量（比如能带）。

---

在第一种FT规范下，

，哈密顿量FT之后变为：

其中

。

在第二种FT规范下，

。容易看出，因为

，此时

满足布里渊区的周期边条件：

。而第一种FT规范下

，因为

。

能带作为可观测量，不依赖于规范的选取。设

，两种规范下色散都是

Dirac点出现在布里渊区边界点

。

但第一种FT规范下，因为

，所以求出来的波函数也没有周期性：

。在计算陈数时，如果波函数在布里渊区边界不连续，则需要额外考虑不连续性带来的积分贡献。（Bernevig的拓扑教材Graphene那一章开头也讲到了这个规范变换，不过说的比较简略。）

---

以上推导是用产生消灭算符来写的，产生算符

指的是在

处的a点产生一个电子，

则是消灭一个电子。这里已经预先选取了电子的轨道，hopping强度

取决于轨道的交叠积分。下面直接用原子轨道来写，更容易理解一些。

设六角格子每个点只有一个电子，轨道波函数为

，将其组合成Bloch波函数（也就是FT):

式中

是每个原胞的坐标（也就是A点的位置），

是B点的位置(

是A到B的平移矢量），这样组合出来的Bloch波函数就分别对应A点和B点的波函数。注意到Bloch组合系数

是原胞坐标，所以对应前面说的第二种FT规范。

将两个Bloch轨道简记为

。总的波函数是这两个轨道的线性组合：

，本征方程为

。左边分别乘以两个Bloch轨道，将方程化为矩阵的形式：

其中

。当只考虑最近邻相互作用时，因为同种原子没有最近邻，对角项

只有同个原胞内轨道的交叠的贡献，

为常数。非对角项有三个最近邻原胞非同种原子的贡献：

式中

表示三个最近邻，

是交叠积分，所以

。上面推导第二个等号中

，因为

遍历所有格矢，当固定

时，

只是

的一个重新排列，所以可以将对n求和改为

求和。S矩阵可设为单位矩阵。这样，除了多了一个常数矩阵

（只上下平移能带，不改变形状），哈密顿量化为与之前完全相同的形式。

哈密顿量解出来的波函数实际是两个Bloch轨道的组合系数。如果要考虑波函数的对称性，还需要考虑所选取轨道的对称性。

---

2. Honeycomb lattice对应的“砖块格子”（brick lattice）

六角格子看起来有点复杂，尤其是不容易切出一块来，让它还能周期连接。这里介绍一下所谓的brick lattice，就是把六角格子拉平了，方便用直角坐标写出每个节点位置，想要周期连接或者取开边界也容易看。

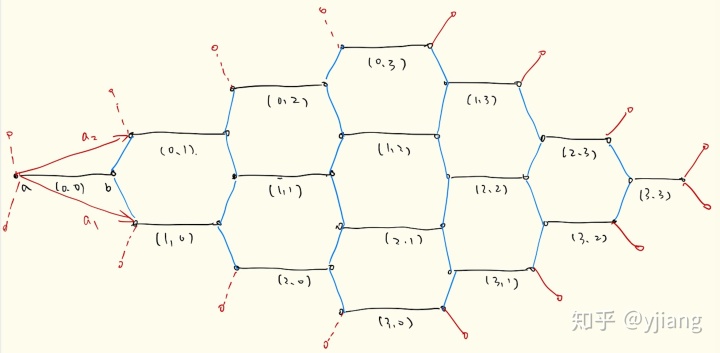
以下面两张图为例，分别是brick lattice和对应的Honeycomb lattice。图中画了4*4个原胞（3*3个六边形），蓝色框是一个原胞，每个原胞用

标记。上边和右边红色的边是周期连接的边，连到下边和左边（为了方便看，第二张图里还用红色虚线画出了连过去的位置）。

每个原胞的位置为

，

是原胞在六角格子里的真实坐标，

是brick lattice里的坐标。做FT时只需要用

即可。

当原胞基矢取不同规范时，相应的六角格子和砖块格子的形状也会发生变化。

3. 六角格子开放边界的不同取法

六角格子可以取zigzag, bearded, armchair等边界条件，并且对应不同的边界态，可以参考文章：
Ryu S, Hatsugai Y. Topological origin of zero-energy edge states in particle-hole symmetric systems[J]. Physical review letters, 2002, 89(7): 077002.

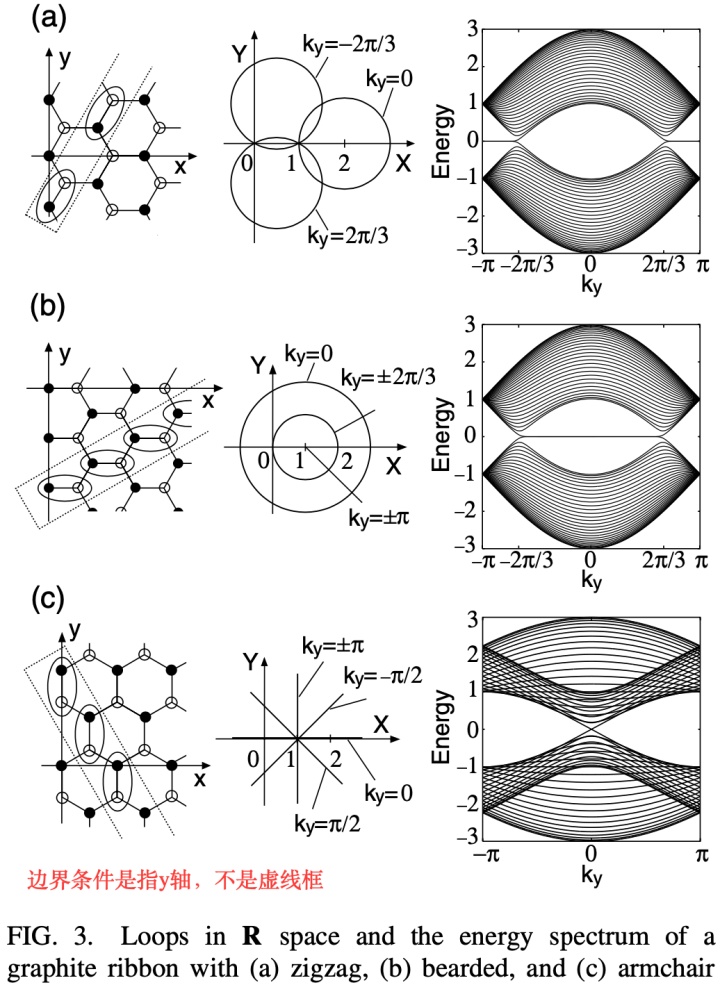
待续。。

4. Slab模型求解

对二维系统，如果x方向是周期的，y方向取N层的开边界，考虑两带模型，这样波函数为

，其中下标数字表示y方向第n层。写出来的slab哈密顿量就是一个

维的矩阵（只考虑相邻层的耦合）：

其中每个

是

矩阵，对角元

是描述每层内部的哈密顿量，上次对角元

描述与上面一层的耦合，下次对角元

描述与下面一层的耦合，其余矩阵元都为0。

是N维单位矩阵，

（

）是上（下）次对角线为1的N维矩阵。

很容易从原来周期系统中读出来。这样一个矩阵可以很方便地用代码(python)写出来：

H= np.kron(np.diag(np.ones(N)),H0) + 
   np.kron(np.diag(np.ones(N-1),1),H1) + 
   np.kron(np.diag(np.ones(N-1),-1),np.conjugate(np.transpose(H1)))

以前面的Honeycomb模型为例，取格矢

方向周期，

方向开边界，则有

第n层A、B格点波函数满足的方程可以显式写出：

参考前面的brick lattice，第一个关于A的方程里，

项表示与同一个原胞内B之间跃迁，

项表示与左边相邻原胞内B的跃迁（所以要乘上Bloch因子，表示向左平移一个原胞里B的波函数），

项表示与下面一层的B的跃迁。

表面格林函数严格求解：待续。。