 | 扫码查看下载
全部资源
|  | ||
北师大版七年级数学上册知识点梳理总结
北师大版七年级数学上册知识点精讲
北师大版七年级数学下册知识点精讲
北师大版七年级数学上册全册教案
第一章 丰富的图形世界
1.1 生活中的立体图形
1.2 展开与折叠
1.3 截一个几何体
1.4从三个方向看物体的形状
第二章 有理数及其运算
2.1 《有理数》
2.2《数轴》知识精讲
2.3《绝对值》2.4 有理数的加法2.5 有理数的减法2.6有理数的加减混合运算2.7 有理数的乘法 2.8 有理数的除法2.9有理数的乘方2.10 科学计数法
2.11 有理数的混合运算
2.12用计算器进行运算
第三章 整式及其加减3.1 字母表示数 3.2 代数式 知识精讲3.3《整式》知识精讲3.4 整式的加减3.5 探索与表达规律 第四章 基本平面图形知识点总结
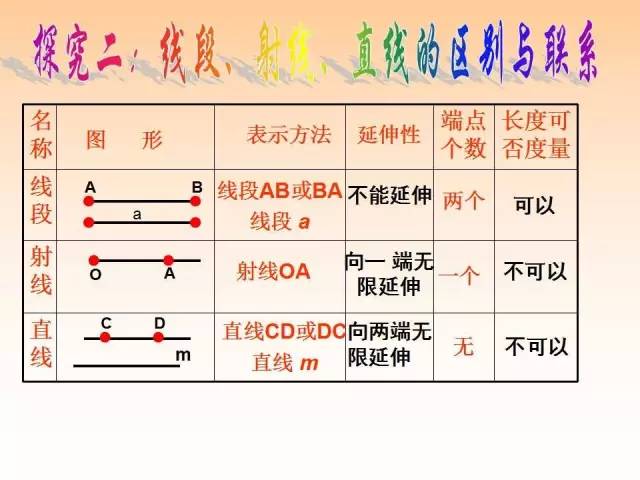
一.直线、射线、线段三者的区别与联系:
二.线段的中点:把一条线段分成两条相等的线段的点,叫做线段的中点。
三.直线的基本性质:
1.两条直线相交,只有一个交点;
2.经过两点有且只有一条直线,即:两点确定一条直线。
四.线段的性质:
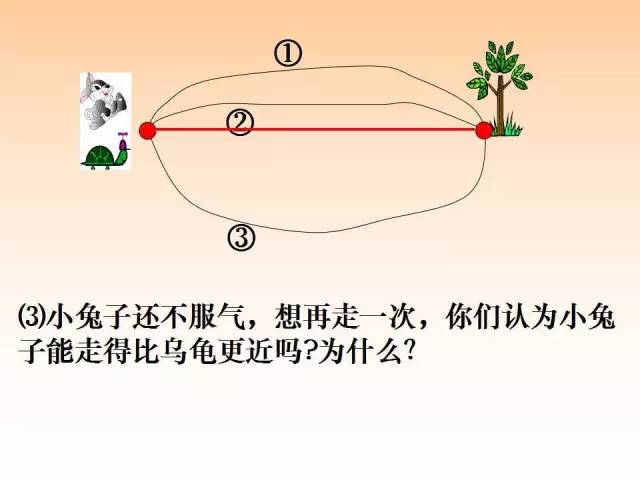
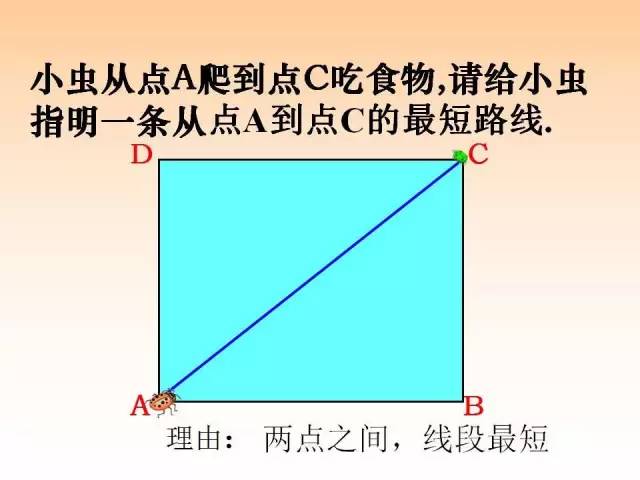
所有连结两点的线中,线段最短,即:两点之间线段最短。
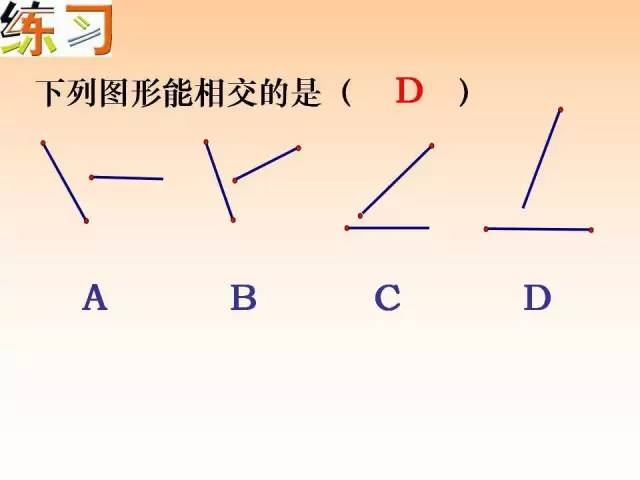
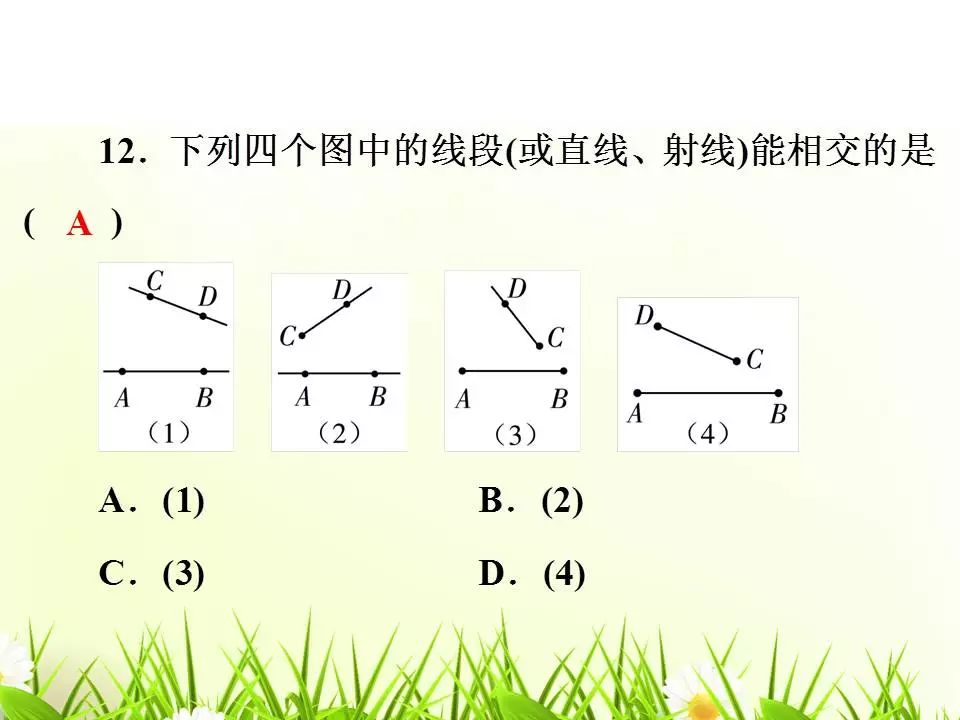
常见考法
(1)确定直线、线段的个数;
(2)求线段的长度。
误区提醒
求线段长度时考虑不周而漏解。
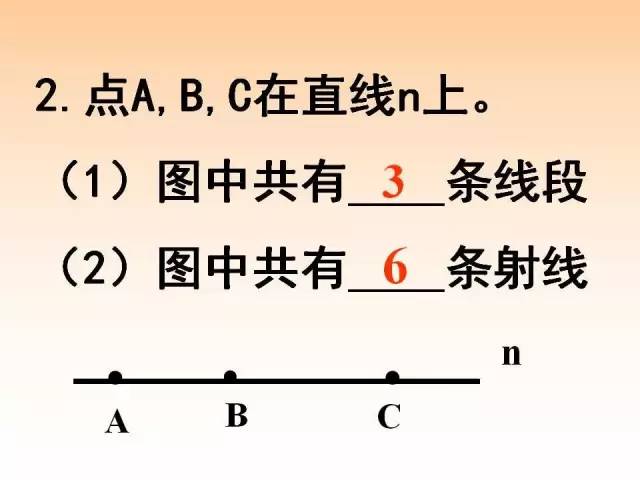
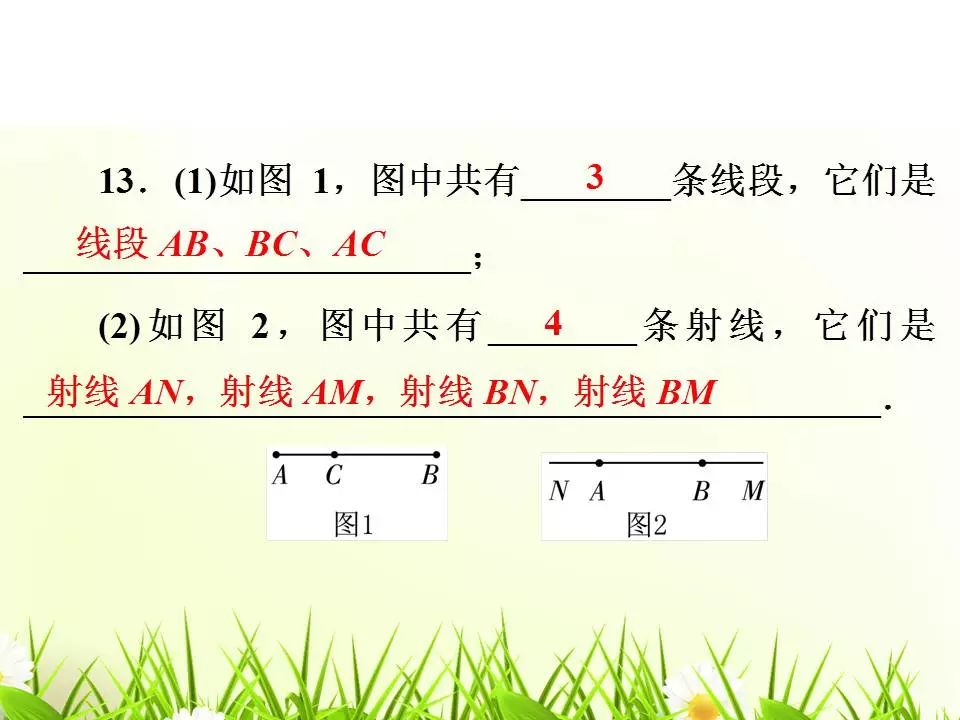
【典型例题】(2010广西柳州)如图,点A、B、C是直线l上的三个点,图中共有线段条数是 ( )
A.1条 B.2条 C.3条 D.4条
【解析】有三条线段,分别是线段AB,BC,AC,故本题选C。
专题精析
一、概念全解
1、基本事实1:两点之间,线段最短.
2、距离定义:两点之间线段的长度叫做两点之间的距离
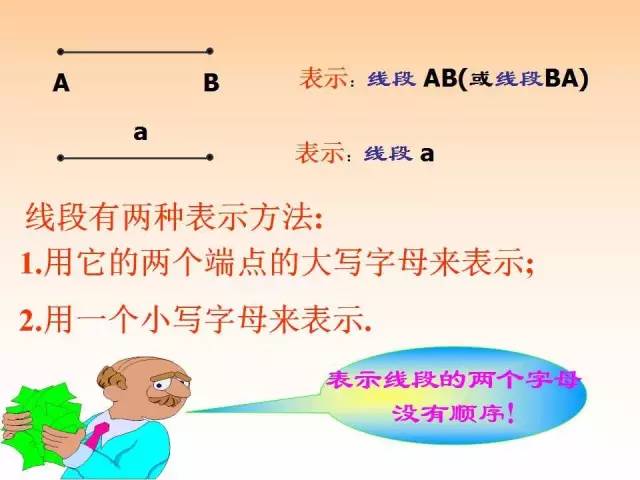
3、线段的两种表示方法:
(1)用两个端点的大写字母:线段AB(线段BA)
(2)用一个小写字母:线段a
4、射线表示方法:
用两个大写字母,端点在前:射线AB(A为端点)
5、同一射线的两同:同端点,同方向
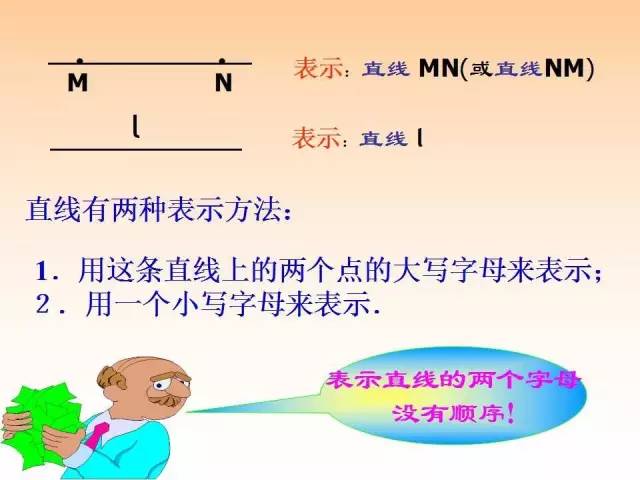
6、直线的两种表示方法:
(1)用两个大写字母:直线AB(直线BA)
(2)用一个小写字母:直线l
7、线段、射线、直线的联系与区别:

8、基本事实2: 两点确定一条直线.
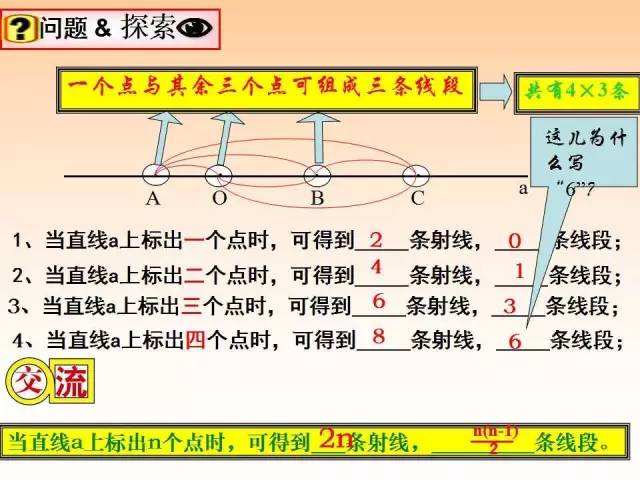
9、平面上,过1点可以画无数条直线,过任意3点可以画1或3条直线.
10、平面上有n个点,

直线上有n个点,

11、点与直线的位置关系:
(1)点在直线上(2)点在直线外
12、线段的长短比较方法:度量法、叠合法、尺规作图法
13、线段的和差
14、线段的中点书写:

二、典例剖析
例:判断正误:
(1)直线AB和直线BA是同一条直线.
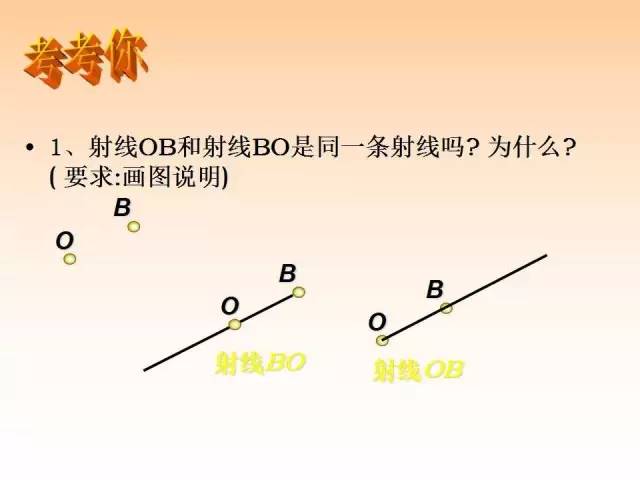
(2)射线AB和射线BA是同一条射线.
(3)线段AB和线段BA是同一条线段.
(4)画直线AB=3cm.
(5)画射线CD=2cm.
(6)延长射线PQ到点R.
(7)延长线段MN到点P.
(8)经过A、B、C三点可以画三条直线.
(9)连接两点的线段叫做两点的距离.
(10)AB=BC,则点B是线段AC的中点.
(11)过两点有且只有一条线段.
(12)已知线段AB=3cm,线段BC=2cm,则A,C两点的距离为5cm.
解析:
(1)正确,直线的两个大写字母顺序可以交换.
(2)错误,同一射线需满足同端点,这里的两个端点分别是A、B.
(3)正确,线段的两个大写字母顺序可以交换.
(4)错误,直线长度不可度量.
(5)错误,射线长度不可度量.
(6)错误,射线只可以反向延长.
(7)正确,线段两端均可延长.
(8)错误,若A、B、C三点在同一直线上,则只能画一条直线.
(9)错误,连接两点的线段的长度叫做两点的距离.
(10)错误,必须强调,点B在线段AC上,否则会出现如下的反例:
(11)错误,过两点有且只有一条直线,否则会出现如下的反例:
过BC的线段有AD,AE两条
(B、C不作为线段端点的情况下)

(12)错误,点C可能在线段AB上,也可能在线段AB的延长线上,也可能在线段AB外,反例如下:
根据三角形三边关系,可得AC的长度范围,1cm≤AC≤5cm.

三、思维提升

1、比例线段求值
例1:
如图,延长线段AB到点C,使BC=2AB,D是AB的中点,点E、F在BC上,且BE:EF:FC=1:2:5,AC=36,求DE和DF的长.

分析:
本题中,已知3条线段长度的比例关系,我们可以马上设x表示3线段的长度,从而可求3线段和的BC的长度,再根据BC与AB的数量关系,表示出AB的长度,建立关于x的方程,从而可求其余线段.
解答:
设BE=x,EF=2x,FC=5x,
∴BC=BE+EF+FC=8x,
∵BC=2AB,∴AB=4x,
∵D为AB中点,∴DB=2x,
AC=AB+BC=12x=36,∴x=3.
∴DF=DB+BE+EF=5x=15.
DE=DB+BE=3x=9.
变式:
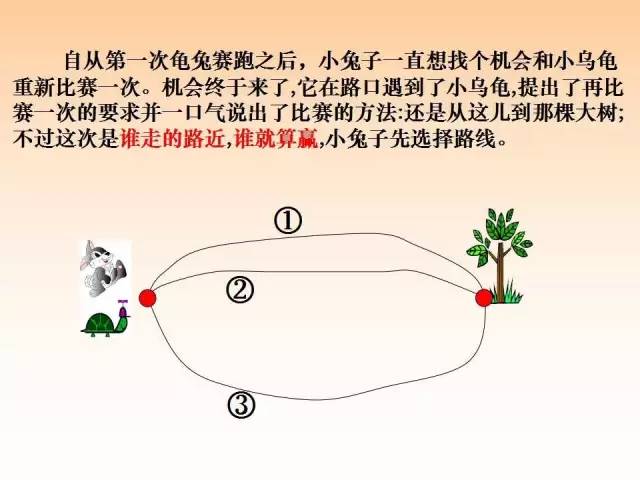
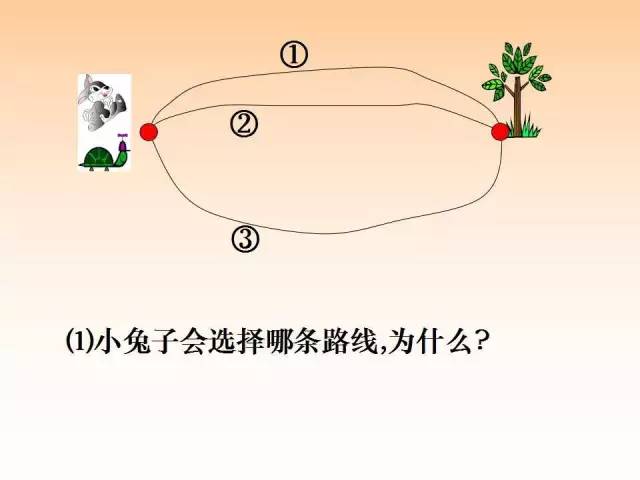
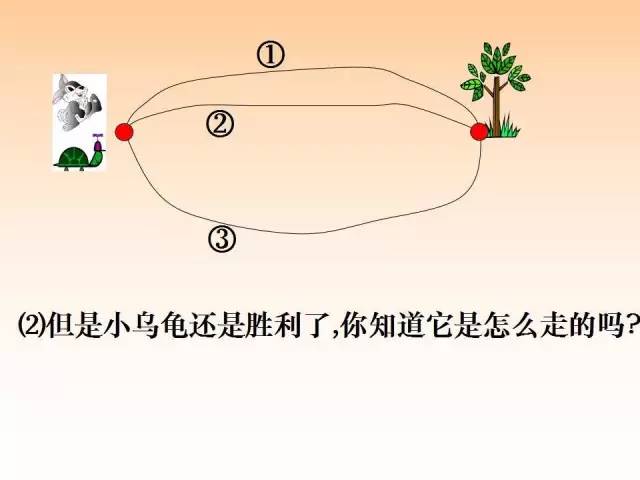
如图,已知AC=200,BC=3AB,且BM:MN=2:3,MN:NC=2:5,求BN的长.

分析:
本题与例1如出一辙,我们可以设x表示AB,BC的长,建立方程求解,再将BM,MN,NC的连比求出,继续设未知数表示从而求解.
解答:


2、多解问题
例2:

分析:
本题中,点C的位置是确定的,但点D的位置不确定,它在直线AB上,可能在线段AB上,也可能在延长线上,因此,可以有2解.
解答:

变式:
已知线段AB=10,M为AB的中点,在AB所在直线上有一点P,N为AP的中点,若MN=1.5,求AP的长.
分析:
本题也与例2类似,M点的位置确定,但N点的位置不定,可能在点M左侧,也可能在点M右侧,因此,本题也有2解,为了让同学们自己思考,笔者就不画图,只给出过程了.
解答:


3、双中点问题
例3:
已知线段AB=8,点M为直线AB上除AB外任意一点,点C是AM的中点,点D是BM的中点,求线段CD的长.
分析:
这是典型的双中点问题,点M的位置不确定,可以在线段AB上,也可以在线段AB的延长线上,也可以在线段BA的延长线上,但是,无论怎样,答案都是不变的!
线段CD的长,必定看作其它线段长的和或差,这里教给大家一个诀窍,点C是AM的中点,点D是BM的中点,这里的点M出现了两次,那么CD的长必然为CM和DM的和或差,不信我们来看解答过程.
解答:

线段、射线、直线的概念及表示
概念:绷紧的琴弦、黑板的边沿都可以近似地看作线段,如果把“线段”作为最简单、最基本原始概念,则用“线段”定义射线和直线如下:
(1)将线段向一个方向无限延长就形成了射线.
(2)将线段向两个方向无限延长就形成了直线.
要点诠释:
(1)线段有两个端点,可以度量,可以比较长短.
(2)射线只向一方无限延伸,有一个端点,不能度量,不能比较大小.
(3)直线是向两方无限延伸的,无端点,不可度量,不能比较大小.
(4)线段、射线、直线都没有粗细.
表示方法:如图1、图2、图3,线段、射线、直线的表示方法都有两种:它们都可以用两个大写字母表示,也可以一个小写字母表示.



要点诠释:
(1)从表示方法上看,虽然它们都可以用一个小写字母表示,也可以用两个大写字母表示,但直线取的是直线上任意两点的字母,线段用的是两个端点的字母,射线用的是一个端点和任意一点的字母,而直线和线段的两个大写字母没有顺序之分,但射线的两个大写字母有顺序之分,第一个大写字母必须是表示端点.即端点相同,而延伸方向不同,表示不同的射线.如下图4中射线OA,射线OB是不同的射线;端点相同且延伸方向也相同的射线,表示同一条射线.如下图5中射线OA、射线OB、射线OC都表示同一条射线.


(2)表示直线、射线与线段时,勿忘在字母的前面写上“直线”“射线”“线段”字样.
3.线段、射线、直线的区别与联系
线段 | 射线 | 直线 | |
图示 |
| ||
表示方法 | 线段AB或线段a | 射线OA或射线a | 直线AB或直线a |
端点 | 两个 | 一个 | 无 |
长度 | 可度量 | 不可度量 | 不可度量 |
延伸性 | 不向两方延伸 | 向一方无限延伸 | 向两方无限延伸 |
练习题
下列说法中,正确的是( ) .
A.射线OA与射线AO是同一条射线.
B.线段AB与线段BA是同一条线段.
C.过一点只能画一条直线.
D.三条直线两两相交,必有三个交点.
【答案】B
【解析】射线OA的端点是O,射线AO的端点是A,所以射线OA与射线AO不是同一条射线,故A错误;过一点能画无数条直线,所以C错误;三条直线两两相交,有三个交点或一个交点(三条直线相交于一点时),所以D错误;线段AB与线段BA是同一条线段,所以B正确.
【总结升华】直线和线段用两个大写字母表示时,与字母的前后顺序无关,但射线必须是表示端点的字母写在前面,不能互换.
举一反三:
【变式1】以下说法中正确的是 ( ).
A.延长线段AB到C B.延长射线AB
C.直线AB的端点之一是A D.延长射线OA到C
【答案】A
基本事实

直线:过两点有且只有一条直线.简单说成:两点确定一条直线.
要点诠释:
(1)点和直线的位置关系有两种:
①点在直线上,或者说直线经过这个点.如图6中,点O在直线l上,也可以说成是直线l经过点O;
②点在直线外,或者说直线不经过这个点.如图6中,点P在直线l外,也可以说直线l不经过点P.
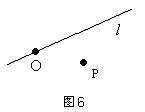
(2)两条不同直线相交:当两条不同的直线只有一个公共点时,称这两条直线相交,这个公共点叫做它们的交点.
2.线段:两点之间的所有连线中,线段最短.简记为:两点之间,线段最短.
如图7所示,在A,B两点所连的线中,线段AB的长度是最短的.
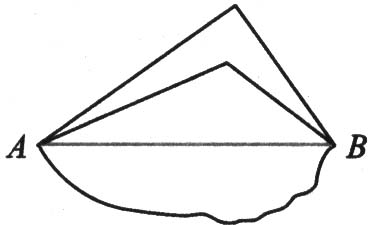
要点诠释:
(1)连接两点间的线段的长度,叫做这两点的距离.
(2)两条线段可能无公共点,可能有一个公共点,也可能有无穷多个公共点.
如图,A、B、C、D为平面内任意三点都不在同一条直线上的四点,那么过其中两点,可画出 条直线.

【思路点拨】根据两点确定一条直线即可计算出直线的条数.
【答案】6条直线
【解析】由两点确定一条直线知,点A与B,C,D三点各确定一条直线,同理点B与C、D各确定一条直线,C与D确定一条直线,综上:共有直线:3+2+1=6(条).
【总结升华】平面上有个点,其中任意三点不在一条直线上,则最多确定的直线条数为:

举一反三:
【变式1】如图所示,已知线段AB上有三个定点C、D、E.

(1)图中共有几条线段?
(2)如果在线段CD上增加一点,则增加了几条线段?你能从中发现什么规律吗?
【答案】
解:(1)线段的条数:4+3+2+1=10(条);
(2)如果在线段CD上增加一点P,则P与其它五个点各组成一条线段,因此,增加了5条线段.
(注解:若在线段AB上增加一点,则增加2条线段,此时线段总条数为1+2;若再增加一点,则又增加了3条线段,此时线段总条数为1+2+3;…;当线段AB上增加到n个点(即增加n-2个点)时,线段的总条数为1+2+……+(n-1)=n(n-1) .)
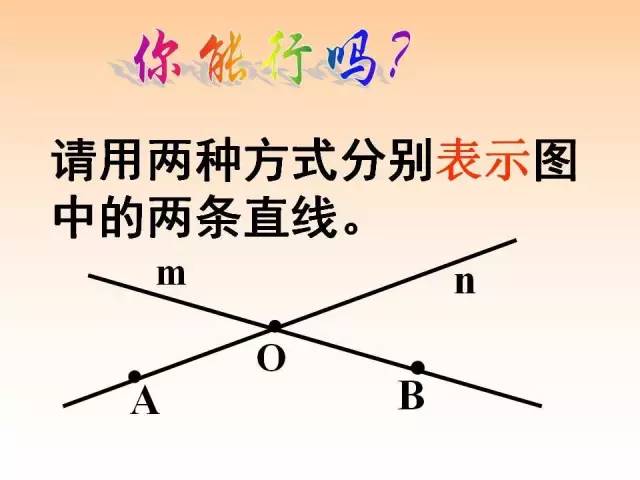
【变式2】如图直线m上有4个点A、B、C、D,则图中共有________条射线.

【答案】8
知识讲解














































图文来自网络,版权归原作者,如有不妥,告知即删
 点击阅读原文下载全册PPT课件动画教案习题整套资料
点击阅读原文下载全册PPT课件动画教案习题整套资料







 这篇内容详细梳理了北师大版七年级数学上、下册的知识点,包括立体图形、有理数及其运算、整式及其加减和基本平面图形等章节。通过例题解析和误区提醒,帮助学生理解概念,如线段、射线、直线的区别与联系,有理数的运算规则,并提供了多解问题和双中点问题的解题方法。同时,还给出了相关练习题和变式题,以巩固学习效果。
这篇内容详细梳理了北师大版七年级数学上、下册的知识点,包括立体图形、有理数及其运算、整式及其加减和基本平面图形等章节。通过例题解析和误区提醒,帮助学生理解概念,如线段、射线、直线的区别与联系,有理数的运算规则,并提供了多解问题和双中点问题的解题方法。同时,还给出了相关练习题和变式题,以巩固学习效果。




















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








