向量交点坐标公式_向量法求二面角的方法——高中立体几何压轴之一

看到一份教案:

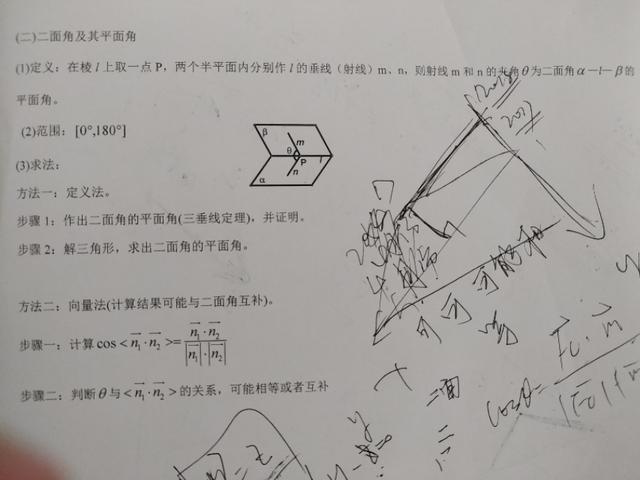
写的还不错，需要有以下补充:

一、简单来说，两个半面所成的角即为二面角α，注意与面面角的区别。

二、向量法相对来说比较容易掌握，步骤如下:

1、建系。以三垂线的交点为原点，没有三垂线时需做辅助线；建立右手直角坐标系，让尽量多的点落在坐标轴上。

2、设点。有时需设线段长为a，写出所有相关的点，一般写四个，两面交线上的两个点M、N加俩面上各一个点A、B。

3、求方向向量。分别求出两面的方向向量AM、AN和BM、BN，带箭头。

4、求法向量m、n，分别设m=(x1，y1，z1)，n=(x2，y2，z2)；利用法向量与方向向量垂直，其数量积为0，可列出两个三元一次方程组；令x1=一个确切的数，比如1或0，求出另外两个坐标，同理可求出n向量(注意法向量需是非零向量)。

5、求出两法向量夹角β，在空间直角坐标系中观察法向量m和n得朝向，朝向面内还是面外。都朝内或都朝外时，α=π-β；一个朝内另外一个朝外时，α=β，如下图:

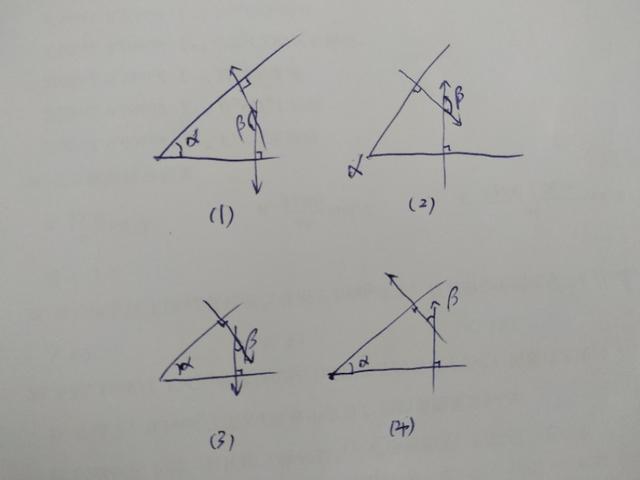
欢迎讨论补充，谢谢。