大一高数下册笔记整理_华东师范大学数学系《数学分析》第4版下册复习笔记和课后习题答案考研真题详解复习答案备考考研资料...

华东师范大学数学系《数学分析》（第4版）（下册）笔记和课后习题（含考研真题）详解

目录

第12章　数项级数
　12.1　复习笔记
　12.2　课后习题详解
　12.3　名校考研真题详解
第13章　函数列与函数项级数
　13.1　复习笔记
　13.2　课后习题详解
　13.3　名校考研真题详解
第14章　幂级数
　14.1　复习笔记
　14.2　课后习题详解
　14.3　名校考研真题详解
第15章　傅里叶级数
　15.1　复习笔记
　15.2　课后习题详解
　15.3　名校考研真题详解
第16章　多元函数的极限与连续
　16.1　复习笔记
　16.2　课后习题详解
　16.3　名校考研真题详解
第17章　多元函数微分学
　17.1　复习笔记
　17.2　课后习题详解
　17.3　名校考研真题详解
第18章　隐函数定理及其应用
　18.1　复习笔记
　18.2　课后习题详解
　18.3　名校考研真题详解
第19章　含参量积分
　19.1　复习笔记
　19.2　课后习题详解
　19.3　名校考研真题详解
第20章　曲线积分
　20.1　复习笔记
　20.2　课后习题详解
　20.3　名校考研真题详解
第21章　重积分
　21.1　复习笔记
　21.2　课后习题详解
　21.3　名校考研真题详解
第22章　曲面积分
　22.1　复习笔记
　22.2　课后习题详解
　22.3　名校考研真题详解
第23章　向量函数微分学
　23.1　复习笔记
　23.2　课后习题详解
　23.3　名校考研真题详解

内容简介

本书是华东师范大学数学系《数学分析》（第4版）（下册）教材的学习辅导书，主要包括以下内容：
1．整理名校笔记，浓缩内容精华。在参考了国内外名校名师讲授该教材的课堂笔记基础上，复习笔记部分对该章的重难点进行了整理，因此，本书的内容几乎浓缩了该教材的知识精华。
2．解析课后习题，提供详尽答案。本书参考了该教材的国内外配套资料和其他教材的相关知识对该教材的课（章）后习题进行了详细的分析和解答，并对相关重要知识点进行了延伸和归纳。
3．挑选考研真题，总结出题思路。本书挑选了部分名校的相关考研真题，总结出题思路，有利于强化对重要知识点的理解。
本书提供电子书及打印版，方便对照复习。

试读（部分内容）

第12章　数项级数12.1　复习笔记
一、级数的收敛性
1级数的定义
若

存在极限值S，即

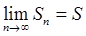
，则级数收敛，S为级数的和。若{Sn}发散，则级数发散。
2重要定理
（1）级数收敛的柯西准则
∑un收敛⇔∀

，∃N（N∈N＋），当m＞N时以及对∀p（p∈N＋），都有

（2）如果级数∑un与∑vn都收敛，则对任意常数c，d，级数∑（cun＋dvn）也收敛，且

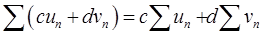
（3）改变级数的有限个项不改变级数的敛散性。
（4）在收敛级数的项中任意加括号，不改变其收敛性与和。
二、正项级数
1正项级数收敛性的一般判别原则
（1）正项级数∑un收敛⇔其部分和数列{Sn}有界。
（2）比较原则
设∑un和∑vn是两个正项级数，∃N（N∈N＋），使得对∀n＞N都有un≤vn，则
①若∑vn收敛，则∑un也收敛。
②若∑un发散，则∑vn也发散。
（3）设S′＝∑un和S″＝∑vn是两个正项级数，如果

则
①若0＜l＜＋∞，级数S′、S″同敛散。
②若l＝0且级数S″收敛，级数S′也收敛。
③若l＝＋∞且级数S″发散，级数S′也发散。
2比式判别法和根式判别法
（1）比式判别法
设∑un为正项级数，且存在正整数N0及常数q（0＜q＜1），则
①若对任意n＞N0，都有un＋1/un≤q，则∑un收敛。
②若对任意n＞N0，都有un＋1/un≥1，则∑un发散。
（2）比式判别法的极限形式
若∑un为正项级数，且

，则
①若q＜1，则∑un收敛。
②若q＞1或q＝＋∞，则∑un发散。
③若q＝1，则无法判断∑un的发散性。
（3）根式判别法
设∑un为正项级数，且存在正整数N0及正常数l，
①若对任意n＞N0，都有

，则∑un收敛。
②若对任意n＞N0，都有

，则∑un发散。
（4）根式判别法的极限形式
设∑un为正项级数，且

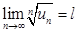
，则
①若l＜1，则∑un收敛。
②若l＞1，则∑un发散。
③若l＝1，则无法判断∑un的发散性。
3积分判别法
设f为[1，＋∞）上非负减函数，那么正项级数∑f（n）与反常积分

同敛散。
三、一般项级数
1交错级数
莱布尼茨判别法
若交错级数满足：①{un}单调递减；②

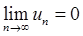
，则级数收敛。
2绝对收敛级数及其性质
（1）若级数∑|un|收敛，则∑un为绝对收敛级数。
（2）绝对收敛级数的性质
①绝对收敛级数一定收敛，但反之却一般不成立，原级数收敛而不绝对收敛的情况，称为条件收敛。
②级数的重排：设级数∑un绝对收敛，且其和等于S，则任意重排后所得到的级数也绝对收敛，且有相同的和数。
3阿贝尔判别法和狄利克雷判别法
（1）阿贝尔判别法
若{un}为单调有界，且∑vn收敛，则级数∑unvn收敛。
（2）狄利克雷判别法
若{un}单调递减且un→0，∑vn的部分和数列有界，则级数∑unvn收敛。