用Java编写约分最简公式_一个有趣的算法问题：如何定义一个分数类

一个来自于C++程序设计的经典问题。如何定义一个分数类，实现分数的约分化简，分数之间的加法、减法、乘法、除法四则运算？

1.初见

刚看到这道题的时候，第一感觉是挺简单的啊，就是基本的面向对象，定义对应的加减乘除类就可以了啊，然而到了实现的时候才发现许多问题是说起来容易做起来难，在实现的过程中，发现了许多的注意点，以及算法。

最终得出结论：这个问题着实是考察程序员基本功的一道好题。

2.整体思路

分数类设计的总体思路如下：

首先是分数的表示，这就需要利用两个变量保存分数的分子和分母；

其次是约分和通分，由于分数四则运算中需要借助约分和通分来实现，因此必须先考虑实现这两个算法。

加法和乘法的实现。利用约分和通分就可以轻松实现。

减法和除法的实现。是加法和乘法的逆运算。和直接转化为加法和乘法。

3.注意事项

负数问题。这个问题十分重要，在我们的算法中，都规定分母为正数，如果出现了分母为负数的情况，就分子分母同时乘以-1，把负数运算放在分子上。

函数的副作用(side effect)。尽量不要在方法中改变原来分数的值，否则会产生副作用，导致后面的运算出错，在代码中会说明。

静态方法和动态方法。和上一点是一样的问题，要确定方式是属于具体的对象，还是属于一个类。

除法运算中，除数不能等于0

4.代码实现

4.1 属性和构造方法

构造方法中有三个细节：一是使用了参数默认值，默认不写参数时，让分子分母都等于1；二是在构造方法中进行了分母合法性的验证，分母等于0时直接返回错误信息；三是对负值进行了处理，使分数的分母永远为正数，方便后续运算。

/**

* 分数运算类

*/

class Fraction

{

//定义分子和分母

public $fenzi;

public $fenmu;

//构造函数

function __construct($fenzi = 1,$fenmu = 1)

{

if ($fenmu == 0) {

return "分母不能为0";

}

if ($fenmu < 0) {

$fenmu = -$fenmu;

$fenzi = -$fenzi;

}

$this->fenzi = $fenzi;

$this->fenmu = $fenmu;

}

}

4.2 最大公约数和最小公倍数

为了后续的约分和通分，必须先求出最大公约数和最小公倍数。求最大公约数采用辗转相除法，而最小公倍数由以下公式可求：

最小公倍数 = (数A * 数B)/ 最大公约数

//求最大公约数用于约分

private static function _getmax($a, $b)

{

if($a < 0) $a = -$a;

if($b < 0) $b = -$b;

$tmp = $a % $b;

while($tmp != 0) {

$a = $b;

$b = $tmp;

$tmp = $a % $b;

}

return $b;

}

//求最小公倍数用于通分

private static function _getmin($a, $b)

{

if($a < 0) $a = -$a;

if($b < 0) $b = -$b;

$max = self::_getmax($a,$b);

$min = intval(($a * $b) / $max);

return $min;

}

/**

* 约分运算，基本算法为分子分母同时除以最大公约数；

* @return void 将对象的分子分母约分为最简形式

*/

public function reduction()

{

$max = $this->_getmax($this->fenzi,$this->fenmu);

$this->fenzi = intval($this->fenzi / $max);

$this->fenmu = intval($this->fenmu / $max);

}

这两个方法全部都定义为静态私有方法，只在类内调用且不需实例化。求最大公约数和最小公倍数的算法其实还有很多种，@烬酱采用了另外一种方法，C++代码如下：

/**

* 求最大公约数并进行约分

* @return void

*/

int reduction()

{

int i,comdiv,small,max;

if(above

{

small=above;

max=below;

}

else

{

small=below;

max=above;

}

for(i=small;i>1;i--)

{

if(small%i==0 &max%i==0 )

break;

}

comdiv=i; //最大公约数

if(i!=0)

{

above/=i;

below/=i;

}

return 0;

}

这种方法的本质就穷尽法，核心思想在于for循环当中。同样的，也可用此法求最小公倍数。

4.3 分数加减

分数加法的算法如下：

/**

* 加法运算，写成静态方法，需要传递两个分数对象实例。加法的基本步骤为：

* 1. 求两个分母的最小公倍数；

* 2. 利用最小公倍数进行通分，此时分母就是最小公倍数，第一个分数的分子等于原来的分子*(最小公倍数/原来的分母)，第二个分数的分子同理；

* 3. 分母不变，分子相加；

* 4. 对结果进行约分；

*

* @param fraction $fra1 分数相加的加数1

* @param fraction $fra2 分数相加的加数2

* @return fraction $fra 分数相加的计算结果

*/

public static function add($fra1, $fra2)

{

$fra = new Fraction();

$min = self::_getmin($fra1->fenmu,$fra2->fenmu);

$fenzi_left = $fra1->fenzi * ($min / $fra1->fenmu);

$fenzi_right = $fra2->fenzi * ($min / $fra2->fenmu);

$fra->fenmu = $min;

$fra->fenzi = $fenzi_left + $fenzi_right;

$fra->reduction();

return $fra;

}

/**

* 减法运算，加法的逆运算，只需要将参数$fra2的分子取反，将减法运算化为加法运算

*

* @param fraction $fra1 分数相减的被减数

* @param fraction $fra2 分数相减的减数

* @return fraction $fra 分数相减的计算结果

*/

public static function minus($fra1, $fra2)

{

$fra_t = new Fraction(-$fra2->fenzi,$fra2->fenmu);

return self::add($fra1,$fra_t);

}

在上述算法中，定义了两个静态方法，每个方法需要传入两个分数对象，之后就可以按上面的算法步骤进行加法和减法运算了。其中减法运算只需要转换为加法即可。需要注意的是，在减法运算中，存在两种可能的写法：

【写法1】

$fra2->fenzi = -$fra2->fenzi;

【写法2】

$fra_t = new Fraction(-$fra2->fenzi,$fra2->fenmu);

其中，第一种写法直接改变了减数分子的值，这里对减法本身的结果不会造成影响，表面上看是成立的，但其实这种写法产生了副作用，在计算乘法时，fra2就已经不是最初的分数值了，因此我们需要new一个新的对象，如写法2所示，这样就不会产生副作用改变分数2的值。

4.4 分数乘除

分数乘数就比较简单了，如下所示：

/**

* 乘法运算，分子相乘，分母相乘之后再约分

*

* @param fraction $fra1 分数相乘的乘数1

* @param fraction $fra2 分数相乘的乘数2

* @return fraction $fra 分数相乘的计算结果

*/

public static function multiply($fra1,$fra2)

{

$fra = new Fraction();

$fenzi = $fra1->fenzi * $fra2->fenzi;

$fenmu = $fra1->fenmu * $fra2->fenmu;

$fra->fenzi = $fenzi;

$fra->fenmu = $fenmu;

$fra->reduction();

return $fra;

}

/**

* 除法运算，乘法运算的逆运算，只需要将参数$fra2的分子分母调换，将除法运算化为乘法运算

*

* @param fraction $fra1 分数相除的被除数

* @param fraction $fra2 分数相除的除数

* @return fraction 分数相除的计算结果

*/

public static function divide($fra1,$fra2)

{

$fra_t = new Fraction($fra2->fenmu,$fra2->fenzi);

$fra = self::multiply($fra1,$fra_t);

return $fra;

}

4.5 分数的表示

最后，我们需要写一个方法，把分数以a/b的形式打印出来。

public function display()

{

printf("%d/%d\n",$this->fenzi,$this->fenmu);

}

这样我们的分数类的定义完了。

5. 结果展示

下面展示运行结果，先写一个调用：

$fra1 = new Fraction(3,4);

$fra1->display();

$fra2 = new Fraction(12,20);

$fra2->reduction();

$fra2->display();

$fra3 = Fraction::add($fra1,$fra2);

$fra3->display();

$fra4 = Fraction::minus($fra1,$fra2);

$fra4->display();

$fra5 = Fraction::multiply($fra1,$fra2);

$fra5->display();

$fra6 = Fraction::divide($fra1,$fra2);

$fra6->display();

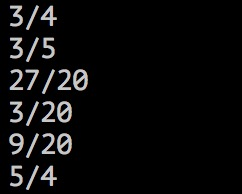
如上，fra1期望直接打印出3/4, fra2对12/20先约分再输出，期望是3/5，fra3是计算fra1和fra2的加法，fra4为减法，fra5为乘法，fra6为除法。结果如下所示：