偏差平方和说明什么_6.7 最大化偏差和double learning

在我们之前所提出的算法中，不管是MC还是TD，一般都遵循广义策略迭代GPI，而在GPI中，为了求得最优策略，在策略提升的时候我们总是使得改进后的策略相对于估计的值函数是贪婪的，所谓贪婪就是最大化的操作。比如Q学习中我们让目标策略的动作为当前状态下动作值函数取得最大的动作。在Sarsa算法中同样也使用了最大化操作。而这个最大化操作会导致严重的正向偏差，我们称之为最大化偏差（maximization bias）。

怎么理解这个正向偏差呢？假设对于一个状态

来说，有很多个动作

可以选择。而每个

真实的值

都为0.但是由于估计偏差或者不确定性导致估计的值

要么大于0，要么小于0.那么对估计值做最大化操作后，就得到了一个正值，显然相对于真实的值0，这是一个正向偏差。

例6.7：最大化偏差举例

考虑如下图所示的一个MDP问题：

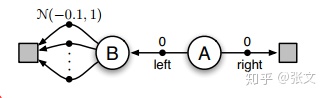
智能体总是从状态A开始，然后具有左右两个动作。向右立马进入终止态并且获得0的回报。向左进入状态B，在状态B有很多个动作，执行任何一个动作都会进入终止并且得到一个服从

的回报。

对于这个问题，显然

.对于任何向左的动作，值函数都为-0.1，即

。为了最大化回报，我们的最优策略应该始终选择向右的动作。可是由于状态B得到的回报是一个分布，我们有很大的概率会在状态B得到一个大于0的回报。那么根据最大化操作，我们就会错误的选择向左的动作。

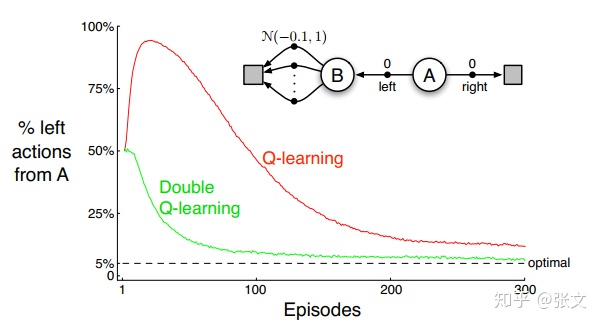
如上图所示，我们会发现在开始阶段，Q学习算法选择向左动作的概率竟然高达90%多，尽管最后收敛到最优。注意这里收敛的时候依然有5%的概率选择向左的动作，这是因为我们采用的是

-贪婪策略。

说明我们有10%的概率随机选择，那么自然的向左向右各有5%的概率。

既然出现这种正向偏差，有没有什么方法能够避免呢？看到上图你肯定知道方法是有的，而且就叫做double-Q学习，那么它的原理是什么呢？

如果我们在考察一下Q学习算法，为了得到更新目标

，我们需要已知两个条件：1）真实的

和2）哪个动作

使得

最大。我们使用了相同的数据来估计这两个条件。这相当于在有最大化偏差（

）的基础上又做了最大化操作。基准都可能是错的，再找最大化的动作就没什么意义了。所以我们要把这两个过程分开。同时估计两个值

和

,然后我们可以用其中一个估计来决定最大化动作，比如

，用另一个估计

来决定状态的值

.这样就无偏了。这就是double learning。值得注意的是，尽管我们有两个估计，但是在一个时间步只会更新一个估计。因此double学习并没有使计算量增加一倍，只是需要增加一倍的内存来存储另一个估计。对于用网络近似值函数的情况来说，就是多了一个网络。

这种思想推广到Q学习算法，就是double-Q 学习，它的更新公式如下：

我们以0.5的概率使用上式更新

，同样的也会有0.5的概率更新

，

的更新公式可以仿照（6.10）给出。double-Q学习算法的效果如上图所示。可以看到最大化偏差的现象明显得到了改善。

整个double Q学习算法伪代码如下：

这两节讲的Q学习算法和double-Q 学习算法都是表格式的。如果我们将其拓展到高维空间，然后用一个近似值函数来替代表格，而如果恰巧这个近似值函数的形式是一个神经网络，我们就得到了DQN和Double-DQN，他们的核心更新步骤是一模一样的。所以说创新也是基于经典。掌握好基础，融会贯通，再适当的做些变通，你就发现创新也不是那么难。我想这也是我坚持写这个笔记的原因。