原文作者:aircraft
为什么引入齐次坐标的变换矩阵可以表示平移呢? - Yu Mao的回答 - 知乎 https://www.zhihu.com/question/26655998/answer/43847213为什么引入齐次坐标的变换矩阵可以表示平移呢? - Yu Mao的回答 - 知乎 https://www.zhihu.com/question/26655998/answer/43847213
在opengl里面涉及到了许多的计算机图形学的知识,当然也涉及到了许多矩阵运算类的知识,基本都是在线性代数里面学过的。
就比如opengl里面的平移函数glTranslatef(x,y,z),
其作用就是将你绘点坐标的原点在当前原点的基础上平移一个(x,y,z)向量。
就是让当前点与一个平移矩阵相乘来求得最终矩阵,来进行平移
那么就要先从矩阵乘法开始
一.矩阵乘法:
若要把矩阵与矩阵相乘,我们要计算行与列的"点积"……这是什么意思?我们来看个例子:
求 第一行 和第一列 的答案:
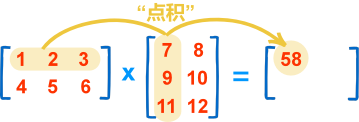
"点积"是把对称的元素相乘,然后把结果加起来:
(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58
我们把第一个元素相配(1 和7),然后相乘。第二个元素(2和9) 和第三个元素(3和11)也一样,然后把结果加起来。
想多看一个例子?这是第一行与第二列:
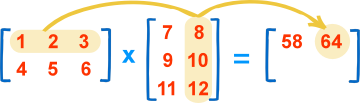
(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64
第二行 和第一列也同样做:
(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139
第二行 和第二列:
(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154
我们得到:
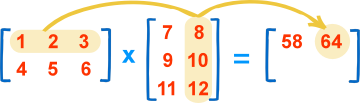
二.矩阵的线性变换以及glTranslatef(x,y,z)函数详解
对于opengl的glTranslatef(x,y,z)函数就是依靠线性变换来进行平移操作的,
其作用就是将你绘点坐标的原点在当前原点的基础上平移一个(x,y,z)向量。
就是让当前点与一个平移矩阵相乘来求得最终矩阵,来进行平移
任意线性变换都可以用矩阵表示为易于计算的一致形式,并且多个变换也可以很容易地通过矩阵的相乘连接在一起。
线性变换不是唯一可以用矩阵表示的变换。R维的仿射变换与透视投影都可以用齐次坐标表示为RP维(即n+1 维的真实投影空间)的线性变换。因此,在三维计算机图形学中大量使用着 4x4 的矩阵变换。
在opengl中就经常用到仿射变换的形式。
仿射变换:为了表示仿射变换,需要使用齐次坐标,即用三向量 (x,y, 1) 表示二向量,对于高维来说也是如此。按照这种方法,就可以用矩阵乘法表示变换。规定:x' =x+tx;y' =y+ty。在矩阵中增加一列与一行,除右下角的元素为 1 外其它部分填充为 0,通过这种方法,所有的线性变换都可以转换为仿射变换。通过这种方法,使用与前面一样的矩阵乘积可以将各种变换无缝地集成到一起。当使用仿射变换时,其次坐标向量w从来不变,这样可以把它当作为 1。
在矩阵的初等变换中,矩阵的左乘代表着行变换,TA=B。
矩阵的右乘相当于列变换, AT=C。
当三维坐标发生旋转、平移时,就需要考虑到矩阵是左乘还是右乘。
设有旋转矩阵R,平移矩阵T, 坐标矩阵A。
-若是绕着静态的世界坐标系旋转,有RA,即左乘旋转矩阵
-若是绕着动态的自身坐标系旋转,有A’R’, 即右乘旋转矩阵
这个意思就是 我们先glTranslatef(x,y,z)移动后旋转的话,那么就是物体先移动 然后绕着自身旋转也是绕自身坐标系旋转。先旋转 在移动 那么就是绕世界坐标系旋转了
好接下来介绍一下矩阵平移
举个二维点移动的例子:
设某点向x方向移动 dx, y方向移动 dy ,[x,y]为变换前坐标, [X,Y]为变换后坐标。
则 X = x+dx; Y = y+dy;
然后其中的矩阵运算过程是:我们先将(x,y)点坐标转化为其次坐标(x,y,1)这是在计算机图形学中经常用到的(不知道为什么要转换为齐次坐标后面会讲)
那么就可以得到:
[ 1 0 0 ]
[X, Y, 1] = [x, y, 1][ 0 1 0 ] ;
[ dx dy 1 ]
这个时候X = x+dx; Y = y + dy; 是不是就实现了坐标的移动???
hhhh 没看懂的话把上面的矩阵乘法在看一次 动动手,写两笔就出来的东西不要一直想
那么在举个三维点移动的例子:
同样的 先(x,y,z)点坐标转化为其次坐标(x,y,z,1) 然后变换后的(X,Y,Z)不就是等于(x,y,z,1)乘以下图的变换矩阵吗???
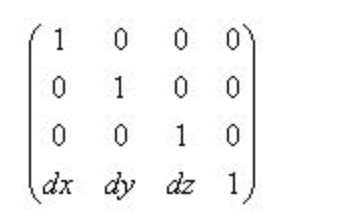
动动手用矩阵乘法得出:X = x+dx; Y = y + dy;Z = z + dz; 不就移动好了吗????
需要特别注意的是在opengl中的矩阵采用列优先存储,矩阵表示如下
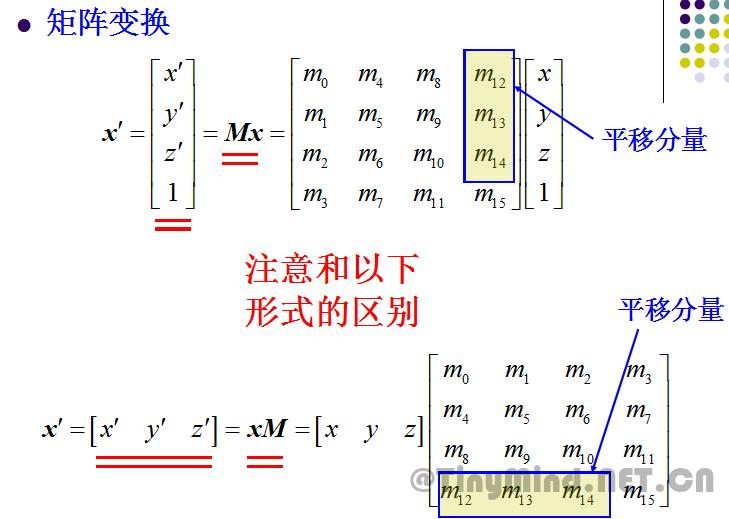
那么刚才为什么要转化齐次坐标??
我们可以看这篇博客:其次坐标的理解
我摘抄主要的部分在下面了:
“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换
对于一个向量v以及基oabc,可以找到一组坐标(v1,v2,v3),使得v = v1 a + v2 b +v3c(1)
而对于一个点p,则可以找到一组坐标(p1,p2,p3),使得p – o = p1 a +p2 b + p3 c(2),
从上面对向量和点的表达,我们可以看出为了在坐标系中表示一个点(如p),我们把点的位置看作是对这个基的原点o所进行的一个位移,即一个向量——p – o(有的书中把这样的向量叫做位置向量——起始于坐标原点的特殊向量),我们在表达这个向量的同时用等价的方式表达出了点p:p= o + p1 a +p2 b + p3 c (3)
(1)(3)是坐标系下表达一个向量和点的不同表达方式。这里可以看出,虽然都是用代数分量的形式表达向量和点,但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7),谁知道它是个向量还是个点!
我们现在把(1)(3)写成矩阵的形式:v = (v1 v2 v3 0) X (a b c o)
p = (p1 p2 p3 1) X (a b c o),这里(a,b,c,o)是坐标基矩阵,右边的列向量分别是向量v和点p在基下的坐标。这样,向量和点在同一个基下就有了不同的表达:3D向量的第4个代数分量是0,而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。
这样,上面的(1, 4, 7)如果写成(1,4,7,0),它就是个向量;如果是(1,4,7,1),它就是个点。下面是如何在普通坐标(Ordinary Coordinate)和齐次坐标(Homogeneous Coordinate)之间进行转换:
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
以上是通过齐次坐标来区分向量和点的方式。从中可以思考得知,对于平移T、旋转R、缩放S这3个最常见的仿射变换,平移变换只对于点才有意义,因为普通向量没有位置概念,只有大小和方向.
而旋转和缩放对于向量和点都有意义,你可以用类似上面齐次表示来检测。从中可以看出,齐次坐标用于仿射变换非常方便。
此外,对于一个普通坐标的点P=(Px, Py, Pz),有对应的一族齐次坐标(wPx, wPy, wPz, w),其中w不等于零。比如,P(1, 4, 7)的齐次坐标有(1, 4, 7, 1)、(2, 8, 14, 2)、(-0.1, -0.4, -0.7, -0.1)等等。因此,如果把一个点从普通坐标变成齐次坐标,给x,y,z乘上同一个非零数w,然后增加第4个分量w;如果把一个齐次坐标转换成普通坐标,把前三个坐标同时除以第4个坐标,然后去掉第4个分量。
为什么引入齐次坐标可以表示平移?
首先我们用一个矢量来表示空间中一个点:
如果我们要将其平移,平移的矢量为:
那么正常的做法就是:
如果不引入齐次坐标,单纯采用3X3矩阵乘法来实现平移
你想做的就是找到一个矩阵
,使得
然后你就会发现你永远也找不到这样的矩阵
所以我们需要新引入一个维度,原来
那么我们可以找到一个4X4的矩阵来实现平移
现在,就有:
三.矩阵实现旋转以及glRotatef(angle,x,y,z)函数详解
函数原型:glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z)
该函数用来设置opengl中绘制实体的自转方式,即物体如何旋转
参数说明:
angle:旋转的角度,单位为度;
x,y,z表示绕着那个轴旋转,如果取值都为0,则表示默认的绕x轴逆时针旋转。
x,y为0,z不为0时,表示绕z轴旋转;x,z为0,y不为0时,表示绕y轴旋转;y,z为0,x不为0,表示绕x轴旋转。
旋转的逆顺时针是通过x,y,z值得正负来确定的:取值为正时,表示逆时针旋转;取值为负时,表示顺时针旋转。
例:glRotatef(30,0,-1,0);
表示绕y轴顺时针方向旋转30度。
关于逆时针与顺时针,可用右手定则:
即手握住某个坐标轴,大拇指指向某轴的正方向,其余四个手指的弯曲方向即为绕某轴旋转的逆时针方向;反之为顺时针方向。
好,看完了函数 我们接下来理解一下矩阵的旋转 当然也包括图形的旋转。。。。
二维极坐标系 情况如下:
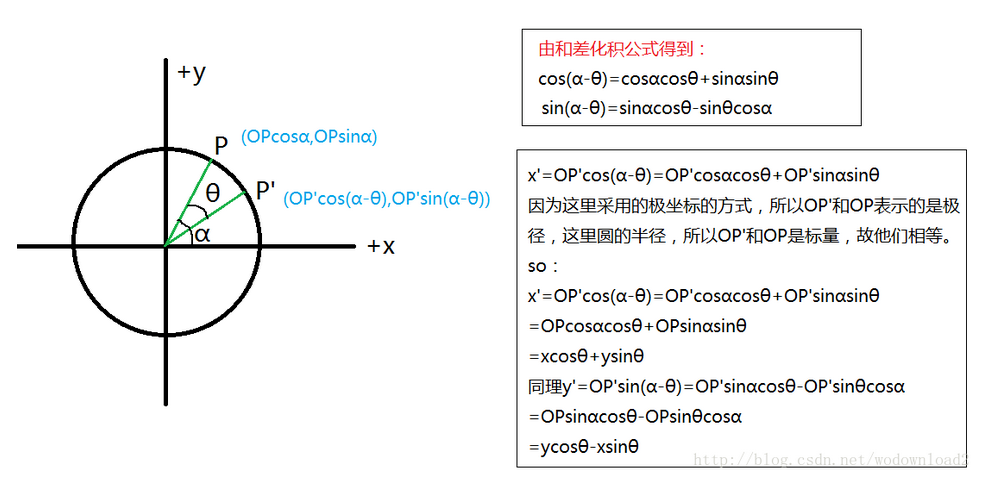
二维情况的旋转c++代码 :
//将空间点绕X轴旋转//输入参数 y z为空间点原始y z坐标//thetax为空间点绕X轴旋转多少度,角度制范围在-180到180//outy outz为旋转后的结果坐标
void codeRotateByX(double y, double z, double thetax, double& outy, double&outz)
{double y1 = y;//将变量拷贝一次,保证&y == &y这种情况下也能计算正确
double z1 =z;double rx = thetax * CV_PI / 180;
outy= cos(rx) * y1 - sin(rx) *z1;
outz= cos(rx) * z1 + sin(rx) *y1;
}
上面是二维的情况,那么我直接想象这是三维的 z轴指向屏幕外,可以上面不就是在三维空间 绕Z轴旋转的情况吗 也就是在XOY面移动 就只改变了x,y坐标
于是可得下面的转换方程
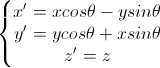 (式一)
(式一)
写成矩阵的形式就是(不理解看 第一步的矩阵乘法知识 在不会敲爆你的狗头!!!)
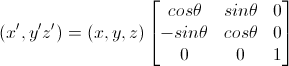
求得旋转矩阵为
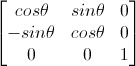
由于这里使用齐次坐标,所以还需加上一维,最终变成如下形式
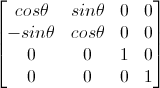
这样就得到了三维空间中绕Z轴旋转的 旋转矩阵式
对于绕X轴旋转的情况,我们只需将式一中的x用y替换,y用z替换,z用x替换即可。替换后得到
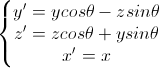 (式二)
(式二)
对应的旋转矩阵为
绕X轴旋转矩阵
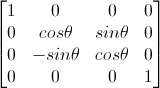
对于绕Y轴旋转的情况,只需对式二做一次同样的替换即可,的到的变换方程为
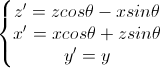
对应的变换矩阵为
绕Y轴旋转矩阵
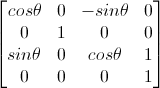
四.如何绕任意轴旋转以及怎么用glRotatef(angle,x,y,z)绕任意轴旋转
绕通过原点的任意旋转轴的旋转是:
glRotatef(theta, vx, vy, vx)
其中vx,vy,vz用与定义通过坐标原点的旋转轴的方向,theta用于指定旋转角度。
如果旋转轴不在原点,可以先用glTranslatef(tx, ty, tz)将旋转轴平移到原点,调用上述函数旋转完成后再平移回原来的地方:glTranslatef(-tx, -ty, -tz)
至于为什么呢 已经有大佬的博客写过整个推导过程 直接推荐给你们:
博客地址是:https://www.cnblogs.com/graphics/archive/2012/08/10/2627458.html
当然为了大家方便看 我直接摘抄主要过来如下:
绕任意轴旋转的情况比较复杂,主要分为两种情况,一种是平行于坐标轴的,一种是不平行于坐标轴的,对于平行于坐标轴的,我们首先将旋转轴平移至与坐标轴重合,然后进行旋转,最后再平移回去。
将旋转轴平移至与坐标轴重合,对应平移操作
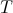
旋转,对应操作
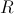
步骤1的逆过程,对应操作
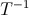
整个过程就是
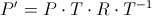
对于不平行于坐标轴的,可按如下方法处理。(该方法实际上涵盖了上面的情况)
将旋转轴平移至原点
将旋转轴旋转至YOZ平面
将旋转轴旋转至于Z轴重合
绕Z轴旋转θ度
执行步骤3的逆过程
执行步骤2的逆过程
执行步骤1的逆过程
假设用v1(a1, b2, c2)和v2(a2, b2, c2)来表示旋转轴,θ表示旋转角度。为了方便推导,暂时使用右手系并使用列向量,待得出矩阵后转置一下即可,上面步骤对应的流程图如下。
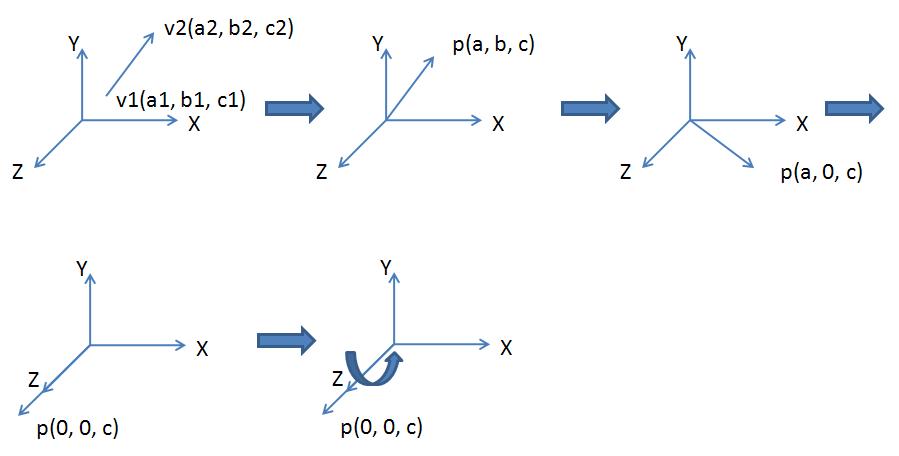
步骤1是一个平移操作,将v1v2平移至原点,对应的矩阵为
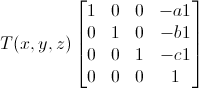
步骤2是一个旋转操作,将p(p = v2 -v1)旋转至XOZ平面,步骤3也是一个旋转操作,将p旋转至与Z轴重合,这两个操作对应的图如下。
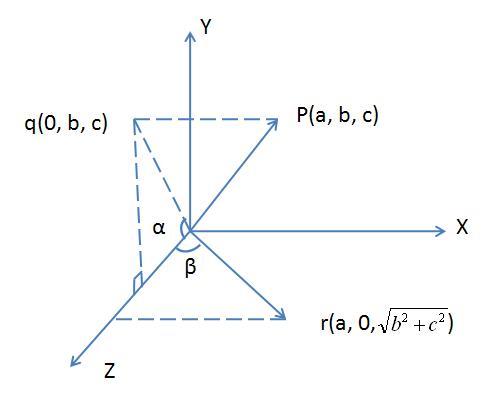
做点p在平面YOZ上的投影点q。再过q做Z轴垂线,则r是p绕X轴旋转所得,且旋转角度为α,且
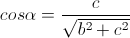 ,
,
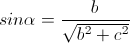
于是旋转矩阵为
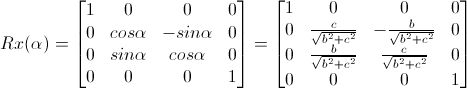
现在将r绕Y轴旋转至与Z轴重合,旋转的角度为-beta(方向为顺时针),且
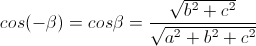 ,
,
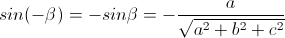
于是得到旋转矩阵为
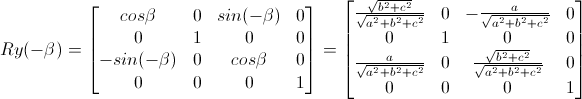
最后是绕Z轴旋转,对应的矩阵如下
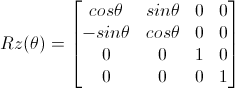
如果旋转轴是过原点的,那么第一步和最后一步的平移操作可以省略,也就是把中间五个矩阵连乘起来,再转置一下,得到下面的绕任意轴旋转的矩阵(这里要注意自己的opengl中是列向量还是行向量 需不要转置这个问题 列向量就不需要转置这一步了)
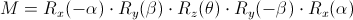
即
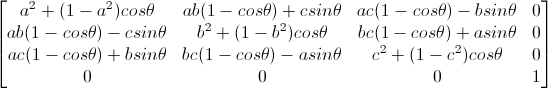
void RotateArbitraryAxis(D3DXMATRIX* pOut, D3DXVECTOR3* axis, floattheta)
{
D3DXVec3Normalize(axis, axis);float u = axis->x;float v = axis->y;float w = axis->z;
pOut->m[0][0] = cosf(theta) + (u * u) * (1 -cosf(theta));
pOut->m[0][1] = u * v * (1 - cosf(theta)) + w *sinf(theta);
pOut->m[0][2] = u * w * (1 - cosf(theta)) - v *sinf(theta);
pOut->m[0][3] = 0;
pOut->m[1][0] = u * v * (1 - cosf(theta)) - w *sinf(theta);
pOut->m[1][1] = cosf(theta) + v * v * (1 -cosf(theta));
pOut->m[1][2] = w * v * (1 - cosf(theta)) + u *sinf(theta);
pOut->m[1][3] = 0;
pOut->m[2][0] = u * w * (1 - cosf(theta)) + v *sinf(theta);
pOut->m[2][1] = v * w * (1 - cosf(theta)) - u *sinf(theta);
pOut->m[2][2] = cosf(theta) + w * w * (1 -cosf(theta));
pOut->m[2][3] = 0;
pOut->m[3][0] = 0;
pOut->m[3][1] = 0;
pOut->m[3][2] = 0;
pOut->m[3][3] = 1;
如果旋转轴是不过原点的,那么第一步和最后一步就不能省略,将所有七个矩阵连乘起来,得到如下变换矩阵
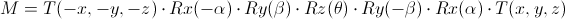
对应如下这个超长的矩阵,在这里(u, v, w) = (a2, b2, c2) - (a1, b1, c1),且是单位向量,a, b, c分别表示(a1, b1, c1)
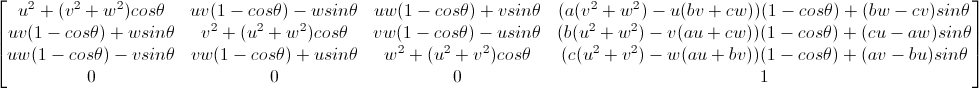
void RotateArbitraryLine(D3DXMATRIX* pOut, D3DXVECTOR3* v1, D3DXVECTOR3* v2, floattheta)
{float a = v1->x;float b = v1->y;float c = v1->z;
D3DXVECTOR3 p= *v2 - *v1;
D3DXVec3Normalize(&p, &p);float u =p.x;float v =p.y;float w =p.z;float uu = u *u;float uv = u *v;float uw = u *w;float vv = v *v;float vw = v *w;float ww = w *w;float au = a *u;float av = a *v;float aw = a *w;float bu = b *u;float bv = b *v;float bw = b *w;float cu = c *u;float cv = c *v;float cw = c *w;float costheta =cosf(theta);float sintheta =sinf(theta);
pOut->m[0][0] = uu + (vv + ww) *costheta;
pOut->m[0][1] = uv * (1 - costheta) + w *sintheta;
pOut->m[0][2] = uw * (1 - costheta) - v *sintheta;
pOut->m[0][3] = 0;
pOut->m[1][0] = uv * (1 - costheta) - w *sintheta;
pOut->m[1][1] = vv + (uu + ww) *costheta;
pOut->m[1][2] = vw * (1 - costheta) + u *sintheta;
pOut->m[1][3] = 0;
pOut->m[2][0] = uw * (1 - costheta) + v *sintheta;
pOut->m[2][1] = vw * (1 - costheta) - u *sintheta;
pOut->m[2][2] = ww + (uu + vv) *costheta;
pOut->m[2][3] = 0;
pOut->m[3][0] = (a * (vv + ww) - u * (bv + cw)) * (1 - costheta) + (bw - cv) *sintheta;
pOut->m[3][1] = (b * (uu + ww) - v * (au + cw)) * (1 - costheta) + (cu - aw) *sintheta;
pOut->m[3][2] = (c * (uu + vv) - w * (au + bv)) * (1 - costheta) + (av - bu) *sintheta;
pOut->m[3][3] = 1;
}
上面代码如果不太会用的话可以用这篇博客的 我觉得写得还不错:

代码为:
#include #include
using namespacestd;#define CV_PI 3.1415926
//定义返回结构体
structPoint3f
{
Point3f(double _x, double _y, double_z)
{
x=_x;
y=_y;
z=_z;
}doublex;doubley;doublez;
};//点绕任意向量旋转,右手系//输入参数old_x,old_y,old_z为旋转前空间点的坐标//vx,vy,vz为旋转轴向量//theta为旋转角度角度制,范围在-180到180//返回值为旋转后坐标点
Point3f RotateByVector(double old_x, double old_y, double old_z, double vx, double vy, double vz, doubletheta)
{double r = theta * CV_PI / 180;double c =cos(r);double s =sin(r);double new_x = (vx*vx*(1 - c) + c) * old_x + (vx*vy*(1 - c) - vz * s) * old_y + (vx*vz*(1 - c) + vy * s) *old_z;double new_y = (vy*vx*(1 - c) + vz * s) * old_x + (vy*vy*(1 - c) + c) * old_y + (vy*vz*(1 - c) - vx * s) *old_z;double new_z = (vx*vz*(1 - c) - vy * s) * old_x + (vy*vz*(1 - c) + vx * s) * old_y + (vz*vz*(1 - c) + c) *old_z;returnPoint3f(new_x, new_y, new_z);
}intmain()
{
Point3f A= RotateByVector(0, 2, 0, 1, 0, 0, 270);
cout<< A.y <
system("pause");return 0;
}
五.结合OpenGL来进行
假如此时我们要让自己的opengl图形原点中心旋转:
那么直接调用 glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z) 即可 不断旋转的话 就直接把angle在其他循环函数中不断加一对360取余数就行了
假如此时我们要让自己的opengl图形在(x,y,z)位置绕自身中心旋转:
那么直接调用glTranslatef(x,y,z)先将物体移动,然后在调用glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z)
假如此时我们要让自己的opengl图形在(x,y,z)位置绕世界坐标系旋转:
那么就是先旋转在移动,先调用glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z),然后在移动到位置 glTranslatef(x,y,z)这也是先移动在旋转 和先旋转在移动的区别,一个绕自身中心旋转,一个绕世界坐标系旋转
此时的 glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z)函数中的 x,y,z 就是一个轴向量了 绕哪个轴旋转的意思 x = 1,y = 0; z = 0;那么就是绕X轴旋转 其他同理 即手握住某个坐标轴,大拇指指向某轴的正方向,其余四个手指的弯曲方向即为绕某轴旋转的逆时针方向;反之为顺时针方向。
假如此时我们要在opengl中绕任意轴旋转,那么跟上面一样,也是先旋转 在移动 此时 glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z)函数 中的x,y,z就是你要绕轴旋转的旋转轴,然后你要在哪里去绕这个轴旋转就在旋转完毕之后就调用glTranslatef(x,y,z)移动到那个位置上就完事了 此时不在原点的话就先glTranslatef(-x,-y,-z)移动回原点 在旋转 然后在移动回去glTranslatef(x,y,z)
参考博客:https://blog.csdn.net/zbq_tt5/article/details/90046527
https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
https://www.zhihu.com/question/26655998/answer/43847213
https://blog.csdn.net/yangmeng900816/article/details/46816007
https://www.cnblogs.com/graphics/archive/2012/08/08/2609005.html
若有兴趣交流分享技术,可关注本人公众号,里面会不定期的分享各种编程教程,和共享源码,诸如研究分享关于c/c++,python,前端,后端,opencv,halcon,opengl,机器学习深度学习之类有关于基础编程,图像处理和机器视觉开发的知识




















 1460
1460











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








