笛卡尔心形线公式表白c语言_听说AP微积分这个重要知识点，可以用来表白？！-"浪漫"的极坐标系...

同学们是否听过这样一个凄美的爱情故事，关于数学家笛卡尔和瑞典公主。在《数学的故事》中，1649年，斯德哥尔摩的街头，52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀，成为了她的数学老师，每天形影不离的相处使他们彼此产生爱慕之心，公主的父亲国王知道后勃然大怒，笛卡尔被流放法国。

流放中的笛卡尔给克里斯汀寄出第十三封信后就气绝身亡了，这第十三封信内容只有短短的一个公式:r=a(1-sinθ)。公主看到后，立即明白了恋人的意图，她马上着手把方程的图形画出来，原来方程的图形是一颗心的形状。这也就是著名的“心形线”。

当然也有人说过这个故事不是真实的，但无论故事的主人公遭遇的真假，心形线确实是存在的，同时笛卡尔也是人类数学史上一颗璀璨的星。在解析几何中我们建立一切方程的基础——坐标系，也正是笛卡尔的杰作。

极坐标转换

但是为何r=a(1-sinθ)被称为心形线呢？或者说怎样建立坐标系才能将这样一个图像绘制出来呢？这就不得不说AP微积分BC中的一个重要内容——极坐标转换。

我们在默认的平面几何表示过程中，经常使用直角坐标系。比如说桌子是一个平面，我们可以在桌角处建立一个直角坐标系（也就是x轴与y轴），此时我们利用x的坐标与y的坐标就可以把桌子上任意一个东西的位置表示出来。

用直角坐标系中的点坐标即可说明物品的位置，直观又方便，但这并不是唯一的方法。极坐标表示形式同样可以表示平面上的任意一点，我们可以在桌子上的中心上建立一个形如八卦阵一样的坐标系，想象我们身处中心处，如果是这样我们要如何能够表达A点的位置呢？

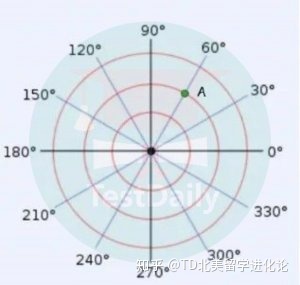
如何表达A点的位置

首先借助方向，可以找到A点在60°的方向上，这时候A便在一条从原点出发，与横向成60°夹角的射线上。再次利用距离，A点距离中心的位置，便可以知道A点在具体什么位置。

这就像投篮，要想把球扔进篮筐，我们需要知道朝哪个方向，并且需要知道距离篮筐有多远。利用这样的信息来表达平面上的点，便是极坐标表达形式了。其中距离记作r，角度记作θ。而上面的心形线r=a(1-sinθ)，不就正是用这两个参数表达的吗？

接下来是如何画这个图像，我们动手画一个r=(1-sinθ)，极坐标图像的画法和常规描点法画图一样，我们取不同的θ值，便会得到不同的r值。根据 θ与r取值的对应变化过程，会产生这样一个轨迹。

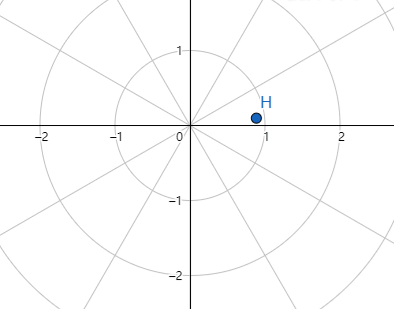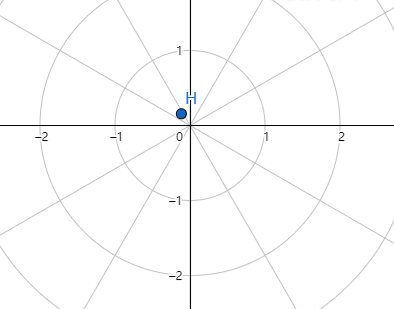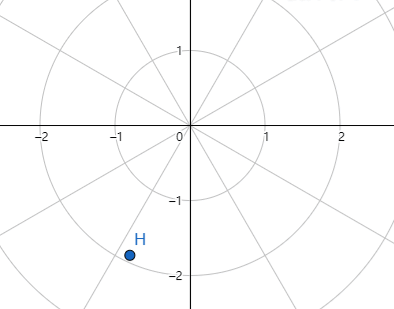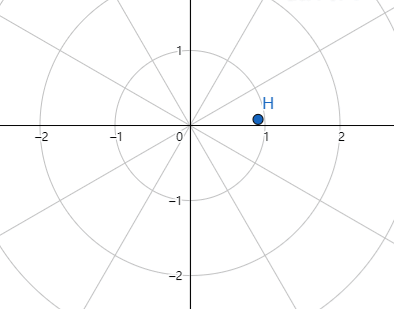
最后把轨迹描绘出来，便是心形线了。

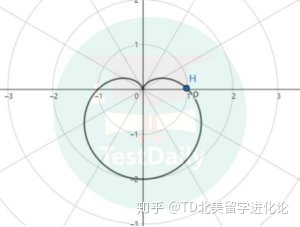
ps：在AP微积分BC考试当中，如果能自己动手画一画极坐标的图像，会令题目变得更加直观，表达式就不再是枯燥的符号了，而且说不准也会是浪漫的形状。

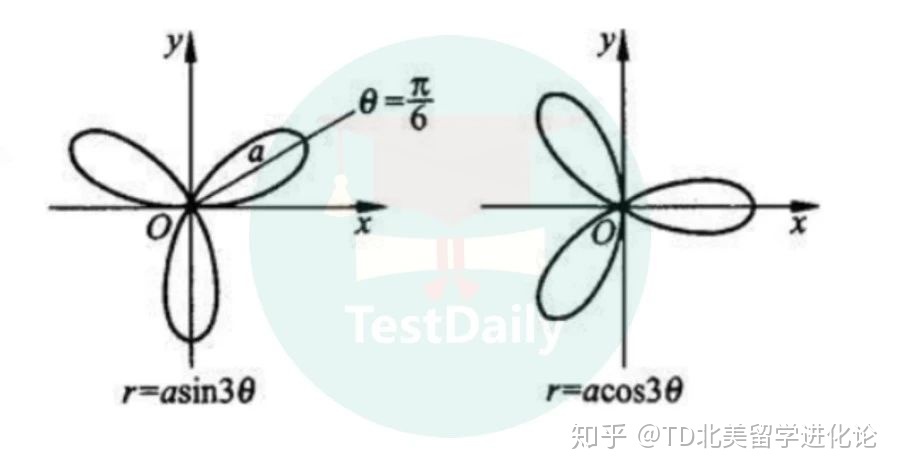
其实心形线只是极坐标系浪漫的一个代表，在极坐标系下，图像通常比直角坐标系圆滑，还有很多的漂亮的曲线可以用极坐标系来表达，比如三叶玫瑰线（2012年的考试中出现了哟）。

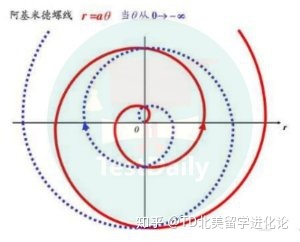
又或者是阿基米德螺线，都是比直角坐标更有趣的曲线哟。

总结

极坐标作为AP微积分BC考试中的重要知识点，总是以大题的形式出现在考试中。总有同学表示对它头疼不已，往往是因为学习的过程并没有体会到它真实的意义。

它可以表示很多无法用直角坐标系进行衡量的曲线，是解析几何的重要工具；同时它的图形又很具魔力，如同上面的阿基米德螺线一般，仿佛能够将视线吸入进去；它颇具难度，也颇具魅力，能帮助我们解决数学难题，同时也能让我们感受到图形的乐趣。

在学习“画圈圈”的过程中，顺便解决掉一个考试难点，也是件不错的事情。

文章作者

TD福利&领取方式

最后是TD送福利时间！为了帮助同学们更好的备考，本次为大家送上的福利是2009-2019年的AP微积分FRQ真题。点击阅读原文，进行领取。