本文是大梦老师的分数巧算教程，详述了分数加减中的凑整抵消技巧，尤其是分数裂项的原理和多种变形，包括裂差和裂和。通过不同难度的例题解析，帮助读者理解和掌握分数计算的高效方法，适用于小升初备考。此外，还涉及乘除法中的分解质因数、乘法分配律、提取公因数等知识点，以及整体约分和换元法的应用。
今天大梦老师给大家梳理一下目前阶段会用到的分数巧算~这个也是拖更很久了~今天也终于在寒假上课前有机会给大家系统的写一写。依然是会一直更新的一个帖子。
更新日志：
19.2.28：更新分数裂项。小升初重点。(已标红)
PS：注意只有从微信公共号底端菜单再次进入这篇文章才能看到更新后的文章哦。
预计全阅读时间：20分钟。
-----------------------------这是美丽的分割线----------------------------
关于巧算，首先大家要意识到，其实巧算无非两类情况，凑整或者抵消，所以很多时候我们都是带着这样的目地去寻找合适的巧算方式。我们简单的按照加减、乘除的分类方式给大家梳理分数巧算。
Ⅰ、加减
情况1：加减凑整和抵消(俗称找好朋友、砍尾巴)
难度：⭐
这类题目在初学分数的时候往往感觉很难，因为分数较为陌生，拿到手后也就只会从左往右依次计算。
本质：先算同分母再算异分母
变形：分组凑整
难度：⭐⭐⭐
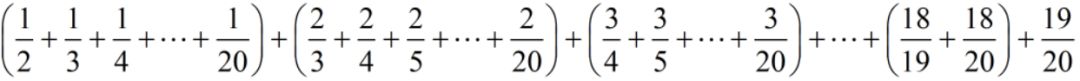
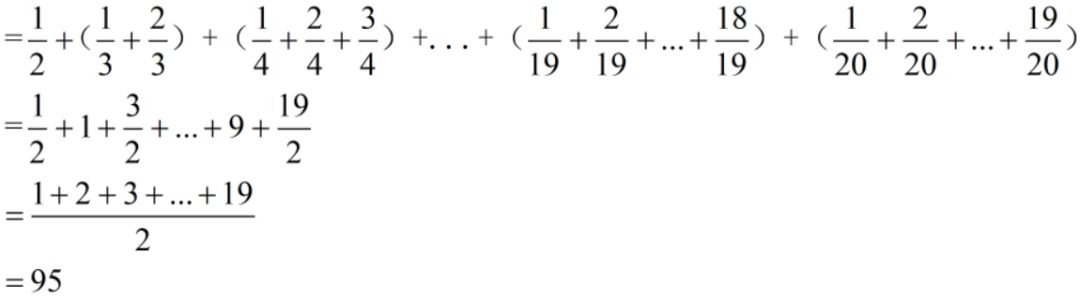
变形：加补凑整(基准数法：主要区别不一定凑的是整十整百的数)
难度：⭐⭐⭐
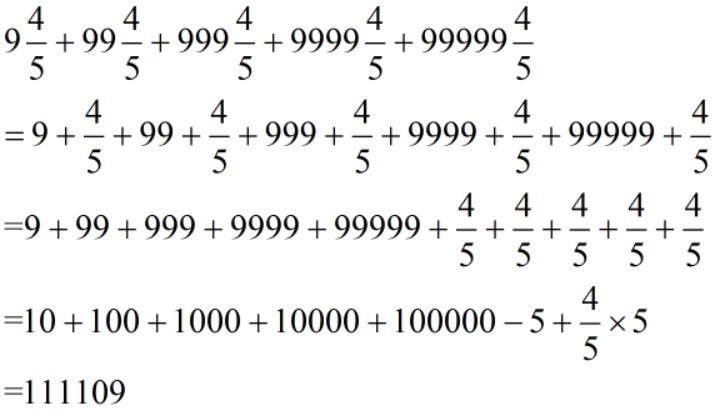
情况2：分数裂项
难度：⭐⭐⭐⭐⭐
分数列项分为裂和和裂差。两者原理相同，但裂差变化更多，小朋友更容易混淆。
本质：分数加减法逆运用。
分了方便大家理解，作为最难掌握的一类题目，我们讲的详细一些。
举一个简单的例题大家就会很清楚了，以下以裂差为例。裂和同理。
分数减法：
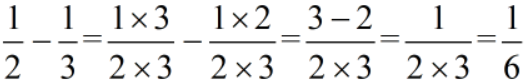
分数裂项：
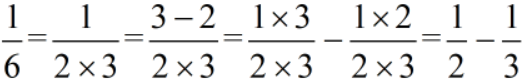
所以不难看出，将分数减法倒过来就是我们的分数裂项了。同时，分数裂项有什么特点呢？当分母为两数相乘，分子为这两个数的差时，我们就可以将其分解为分母这两个数的单位分数相减的形式。
当然同学们就必须要理解了，为什么要拆成单位分数做减法，以及为什么要强调分子为分母这两个数的差呢？
先解决第一个问题。我们刚刚提到，巧算中的一个目的是抵消，而单位分数，是基础的形式，也最容易相同而抵消。
那么为什么非要分子是分母这两个数的差呢？
这就是为了第一个目的了，我们如何拆成单位分数，分什么不把上面的例子中的1看成4-3非要3-2呢，这就是因为当你拆成两个分数做减法的时候，往往分子不为1，只有跟分母有相同数，才能约分变为1，所以我们要求分子必须为分母这两个数的差，从而构造单位分数。
了解到这一点我们就可以回顾一下分数裂项的一些形式了。
ps：易错情况：
✖
情况1：分数裂差
难度：⭐⭐⭐
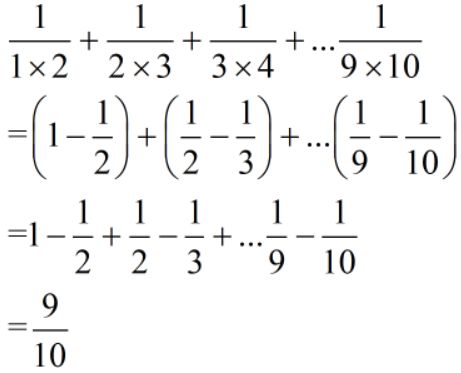
这是一类大家最容易掌握的一类，以下几种变形会越来越难。但一般越难的考频相对会低一些。
变形：
难度：⭐⭐⭐
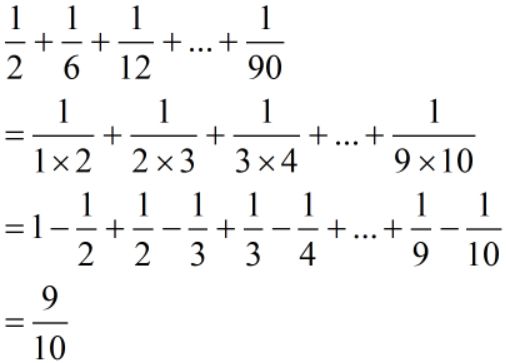
分母写成乘积的形式充满了暗示，但写成乘积就比较困难，所以要对2、6、12、...、90这串连续自然数的乘积特别熟，考频非常高，同时也要知道我们如何将一个分母拆成两数相乘的形式，一定是从左往右依次增大(这样减法才够减)，同时相邻的两个数之间一定要有数相同(这样拆出来的单位分数才能抵消)。
变形：
难度：⭐⭐⭐⭐
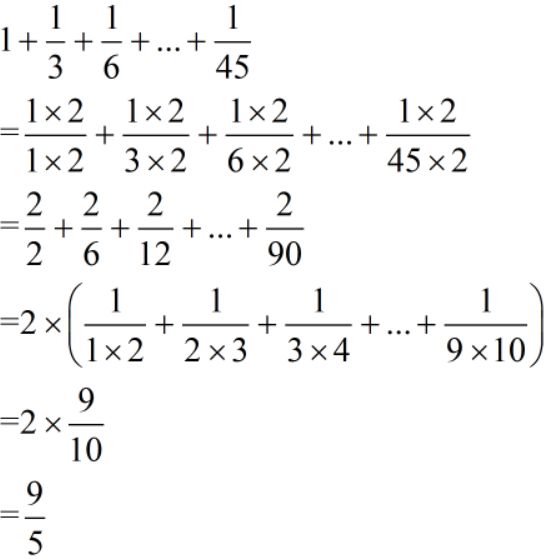
其实这道题的分母很快就会发现拆分有些困难，但是我们会发现它与2、6、12、...、90这串数列有着密切的联系刚好为他们的一半，所以，我们在了解2、6、12、...、90的同时呢也要熟悉1、3、6、...、45这串数列。
变形：
难度：⭐⭐⭐⭐⭐
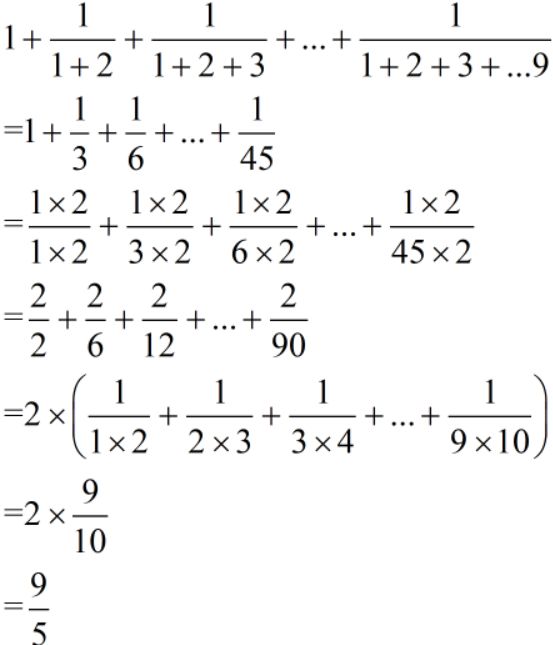
1、3、6、...、45这串数列如果大家熟悉的话就会发现其实他们分别是连续自然数求和之后组成的数列，但大家往往会被它的形式而吓坏，导致不敢做题。这个时候一定要勇敢，做一些“人类本能”的事情，将分母算出来就会发现其实我们还是见过的。
变形：
难度：⭐⭐⭐⭐
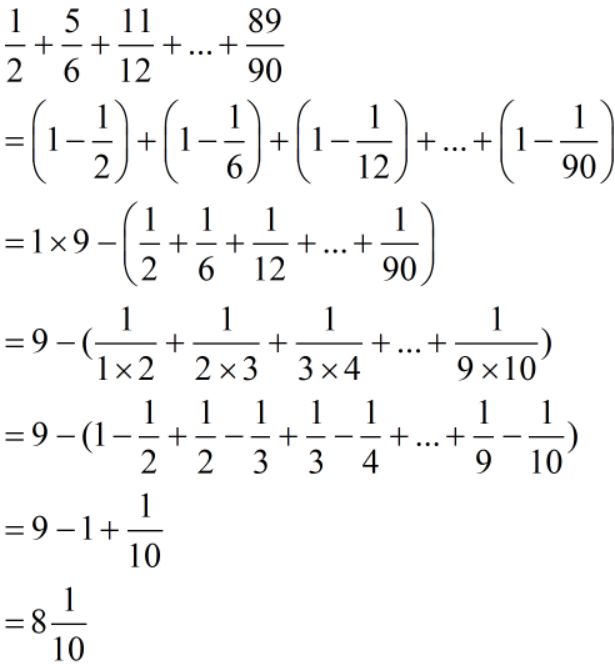
这也是经典的隐藏形式，所以我们要了解这样的变形，这样才能在考试中一击必胜，利用到的还是基准数的原理。
变形：
难度：⭐⭐⭐⭐
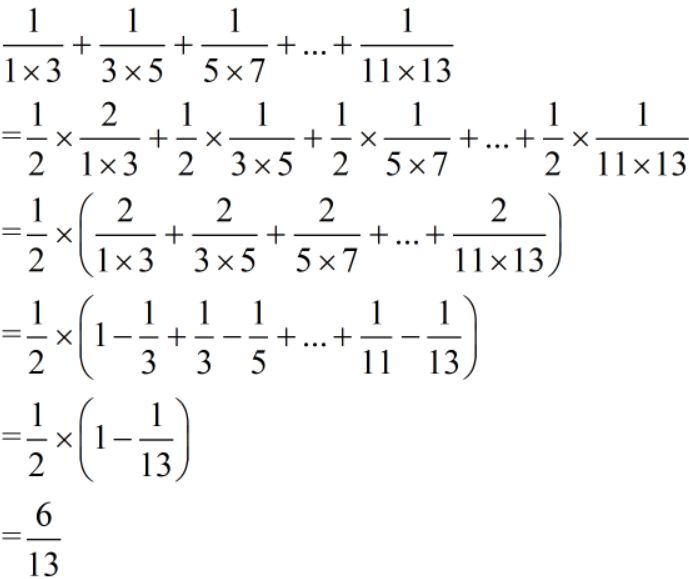
做习惯了分子为1，分母为连续的自然数相乘的题目后，小朋友往往产生了思维惯性，认为凡是分子为1的都可以直接拆分，这是不对的。再次强调一定是分子为分母的差时，才可以直接拆分成单位分数相减。举个例子：
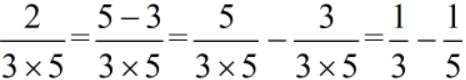
所以我们发现还是之前所强调的，只有分子被写成分母的差时，才能出现与分母相同的数字才能约分成单位分数哦。
所以做这样的题就要先把分子变成差，同时还要保证大小不变，要乘相应的分数。一般为需要的差的单位分数。
变形：
难度：⭐⭐⭐⭐⭐
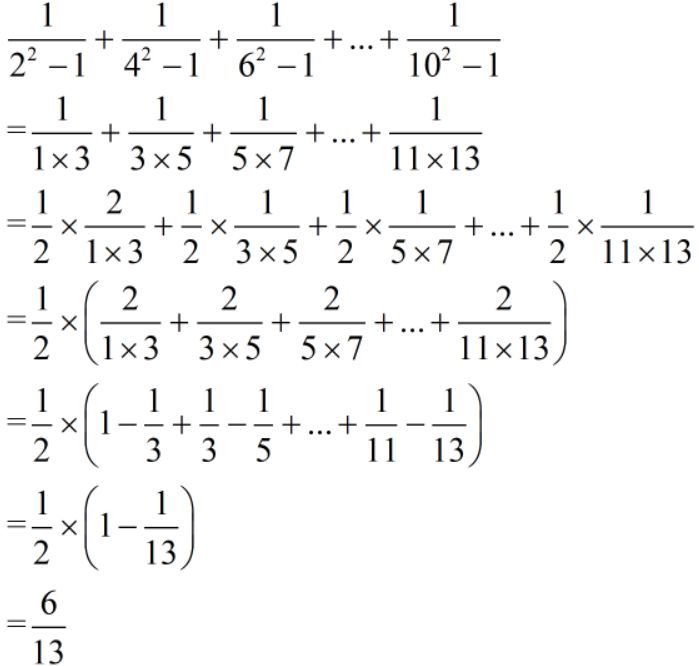
这类题目就是在上一个题目的基础上进行了分母的隐藏，利用平方差公式的特点将其隐藏起来，其实不知道平方差公式也是没关系的，因为我们还是可以做一些“人类本能”的事情。将分母算出来然后拆成两数相乘即可。
变形：
难度：⭐⭐⭐⭐⭐
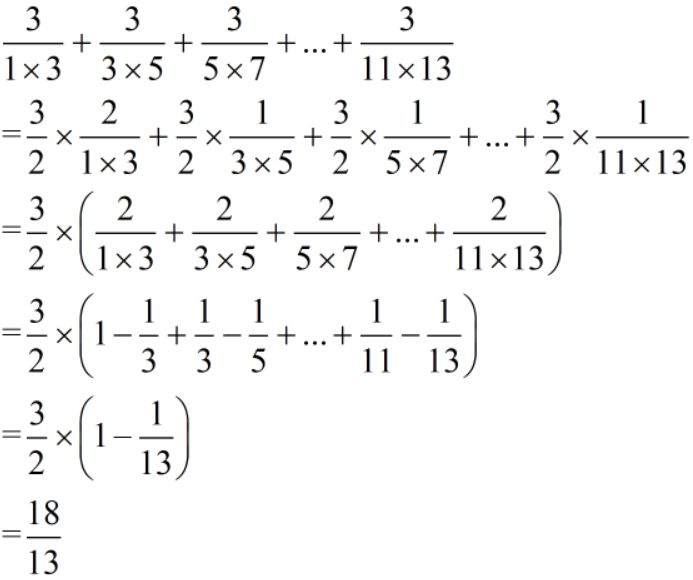
这类题目难点在于分子不是1，进行变形时往往拿不住乘上的分数为多少，这个时候我们要学会把不会的变会的。也就是说我们先把他变为1，再进行操作。分子变为1的过程就是就是提取公因数类似，将分子直接改写成乘积形式即可，例如：
情况2：分数裂和
难度：⭐⭐⭐
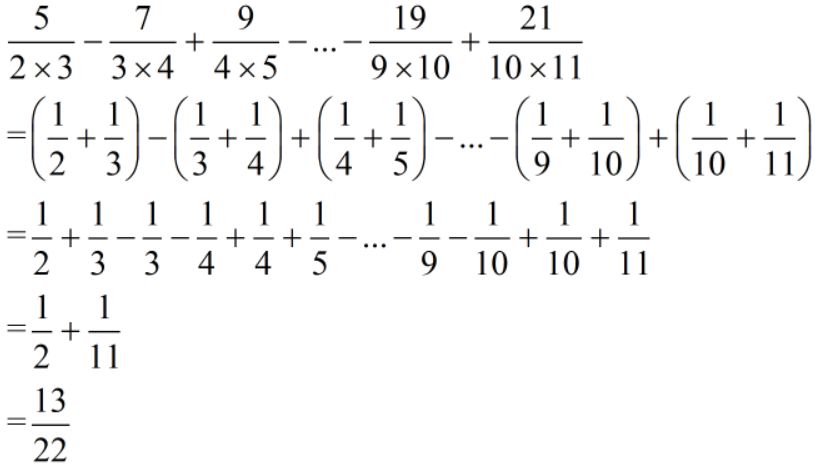
与裂差相同，一旦发现分子为分母两数的和时，就可以拆成单位分数求和。同时由于有减法，所以一定要注意变号的问题。
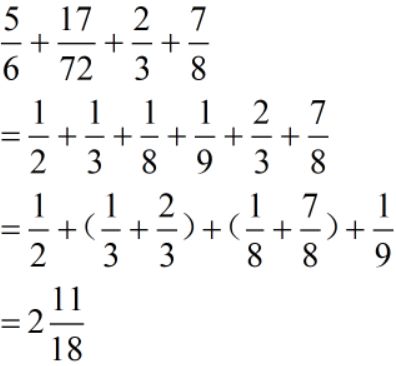
同时，也会出现一些凑整的题目，大家要能够分辨。
变形：
难度：⭐⭐⭐
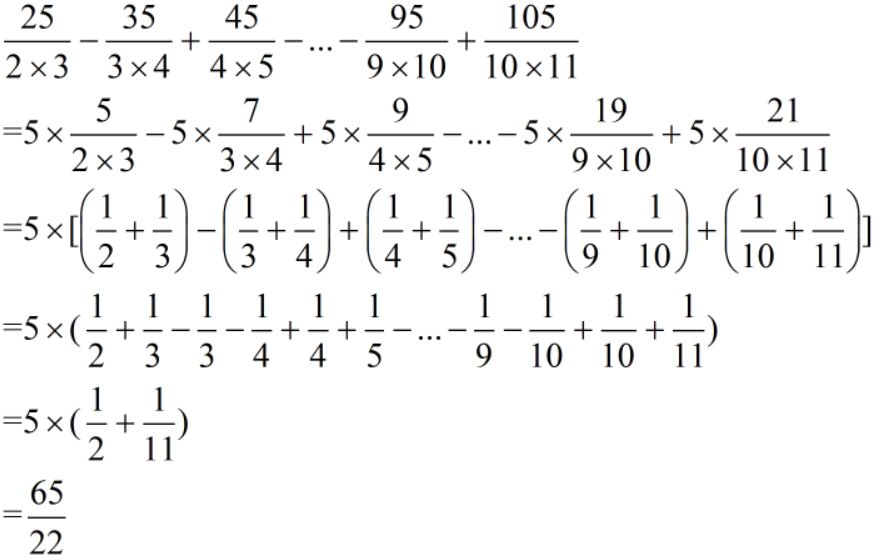
变形大多数也不难，都是成倍数的关系。
3、其它类型
难度：⭐⭐⭐⭐⭐
类型多种多样，视个人情况掌握。在这只分享相对常见的形式。
类型1：
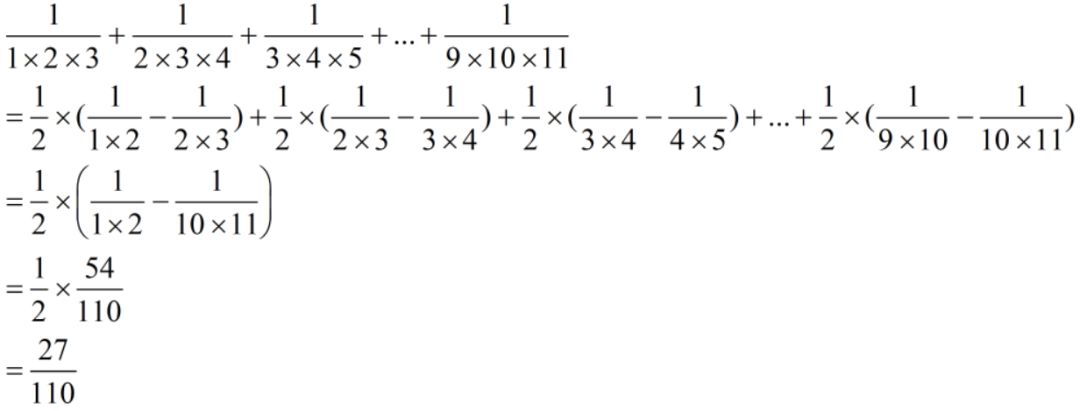
本质依然是构造相同，所以这里有一句话分享给大家，分数裂项两边挑，挑相同，这里以分母为2×3×4的分数为例，往左看相同的为2×3，往右看相同的为3×4，所以最后一定是拆成分母为2×3和3×4的单位分数。
类型2：
这种题主要考察了n！=n×(n-1)！这个性质。所以n！－(n-1)！=(n-1)×(n-1)！。所以就有了构造乘积的方法，同时分子为分母两个数的差。
Ⅱ、乘除法(混合运算)
情况1：分解质因数
难度：⭐⭐⭐⭐⭐(难只难在孩子们不愿意分解大数的质因数或不愿意判断一个大数是不是质数)
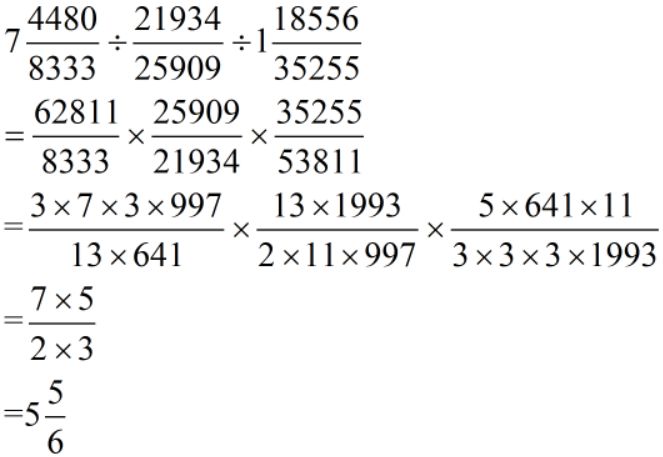
情况2：乘法分配律(简单题不再举例)
难度：⭐⭐⭐⭐
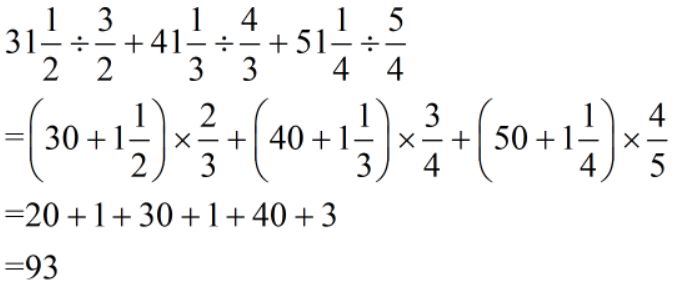
情况3：提取公因数(简单题不再举例)
难度：⭐⭐⭐
变形：用算式表示分子(勉强归为提取公因数，欢迎大家留言对这类题提供你认为合适的分类)
难度：⭐⭐⭐
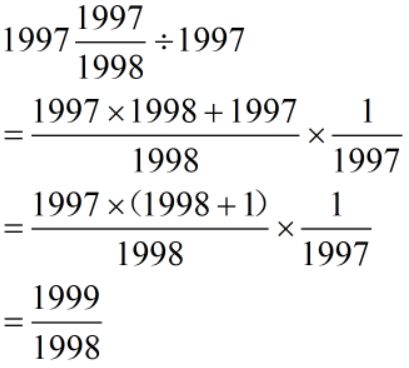
变形：二次提取公因数(算算出奇迹)
难度：⭐⭐⭐
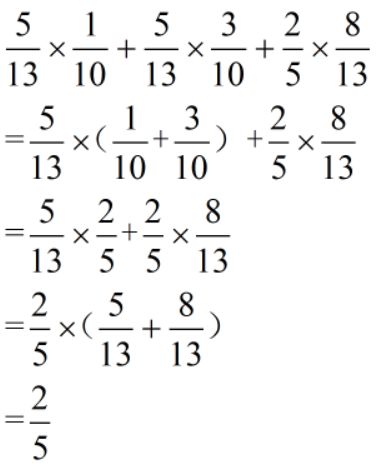
变形：公因数隐藏
难度：⭐⭐⭐⭐
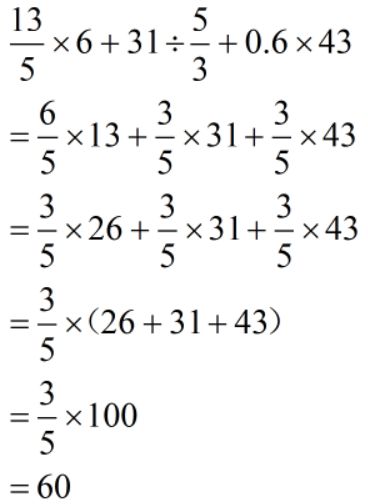
情况4：连锁约分
难度：⭐⭐
变形：(与基准数的关系)
难度：⭐⭐⭐
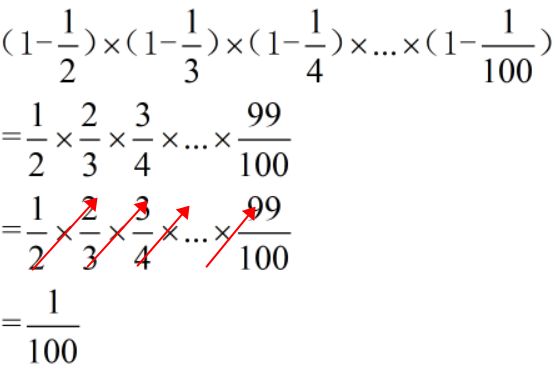
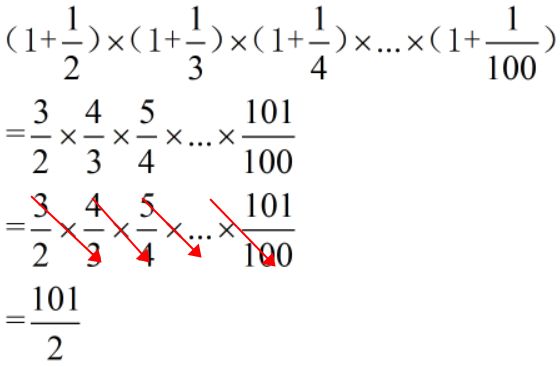
变形：(基准数混合)
难度：⭐⭐⭐⭐
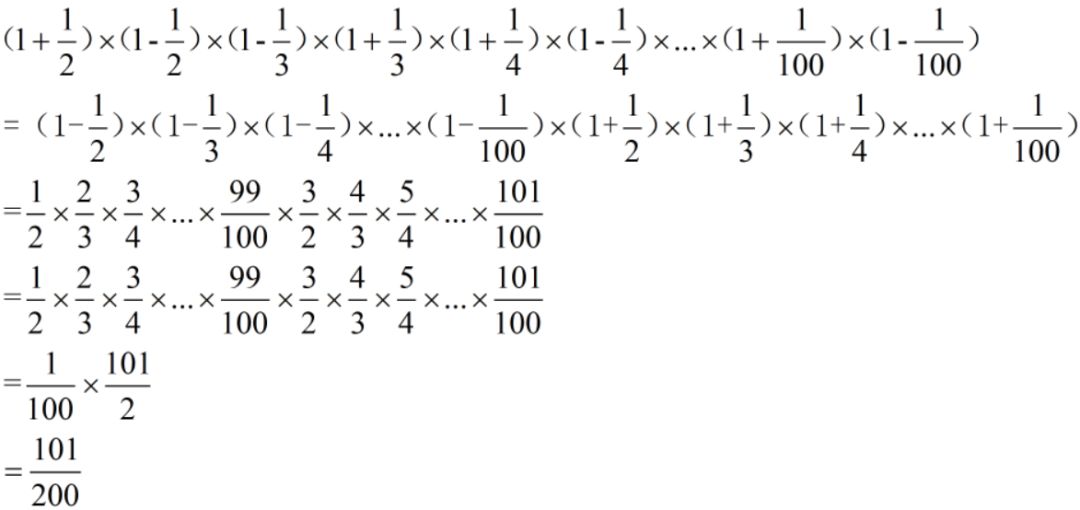
变形：(利用平方差公式)
难度：⭐⭐⭐⭐⭐
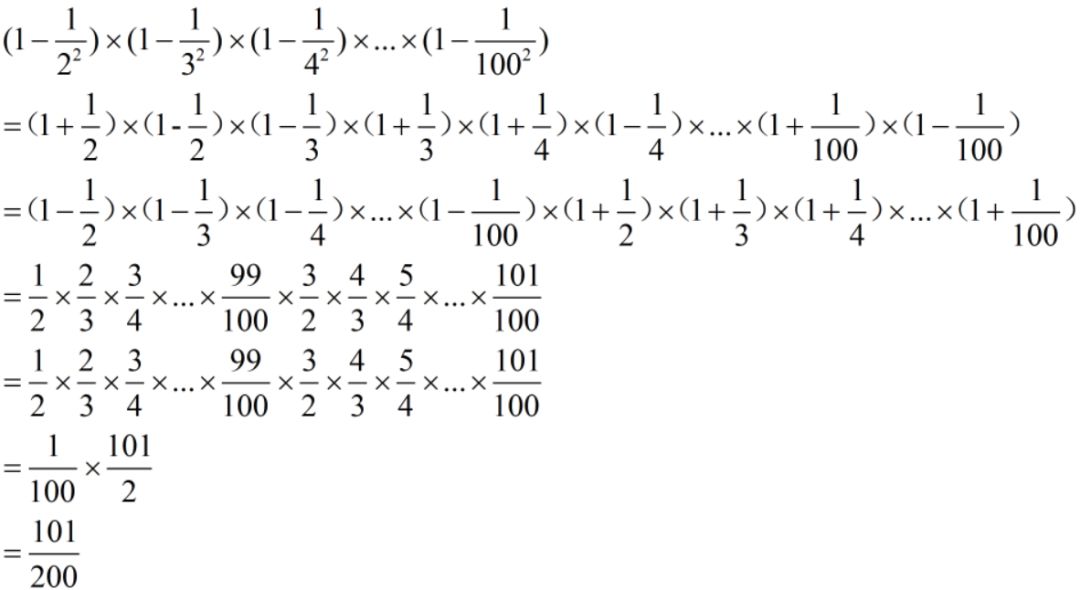
当然也可能进一步变化，比如将括号里面的减法再算一步，如：
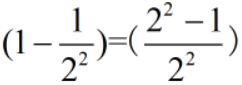
情况5：整体约分
难度：⭐⭐⭐⭐
核心：将分子分母写成乘积形式并有共同部分可以约分。这类问题往往每个括号中出现的分数单位相同。
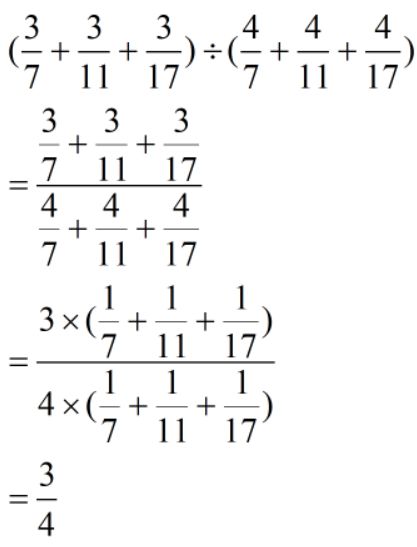
注：转化为繁分数方便看出约分情况
变形：
难度：⭐⭐⭐⭐
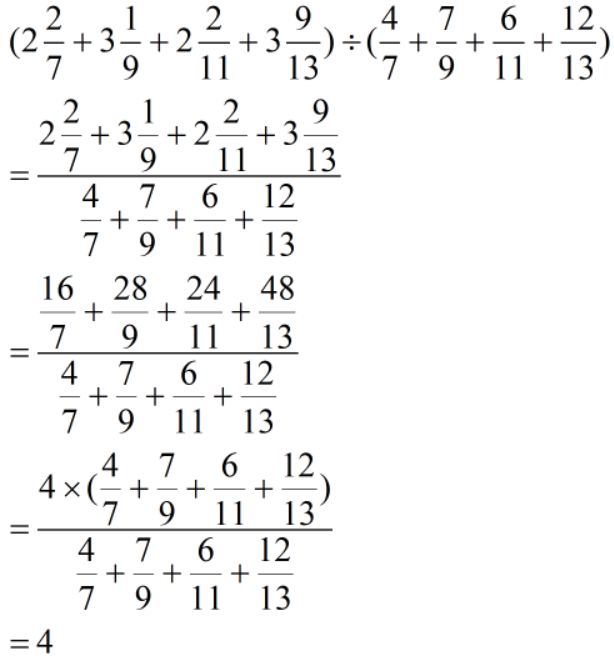
变形：
难度：⭐⭐⭐⭐
注：假化带之后不要进行约分，会改变单位分数，导致看不出整体约分所需要提取的公因数。
变形：
难度：⭐⭐⭐⭐⭐
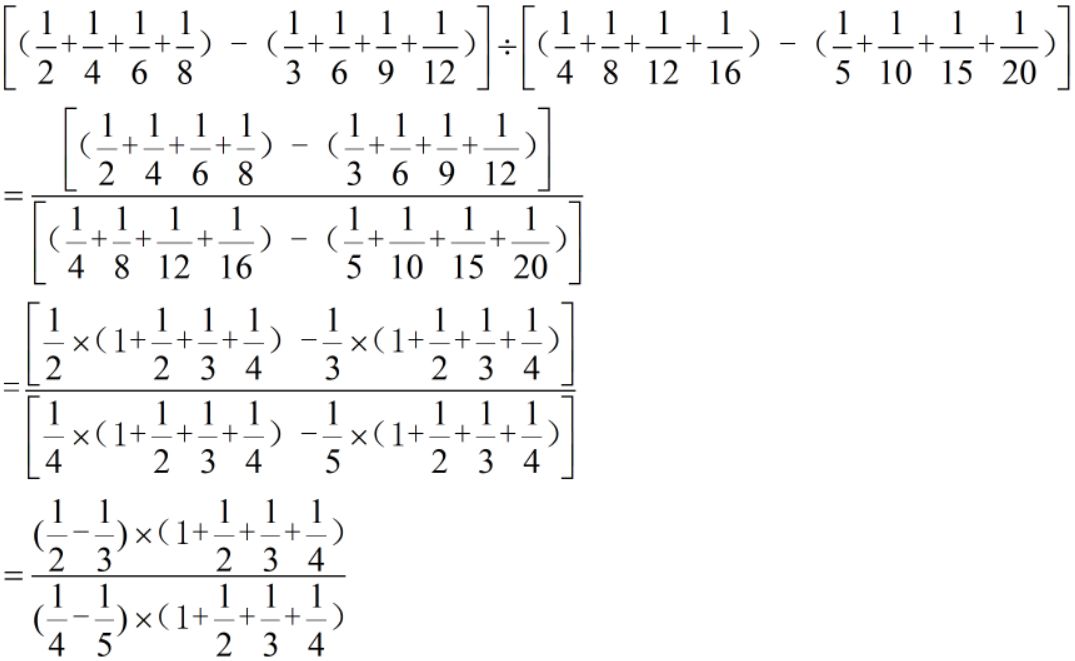
变形：(相当于等比性质)
难度：⭐⭐⭐⭐⭐
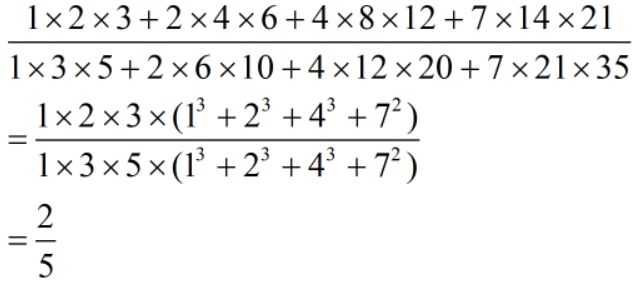
注：先横向比较倍数关系再找到公因数
情况6：换元法
难度：⭐⭐⭐(简单但不好想到)
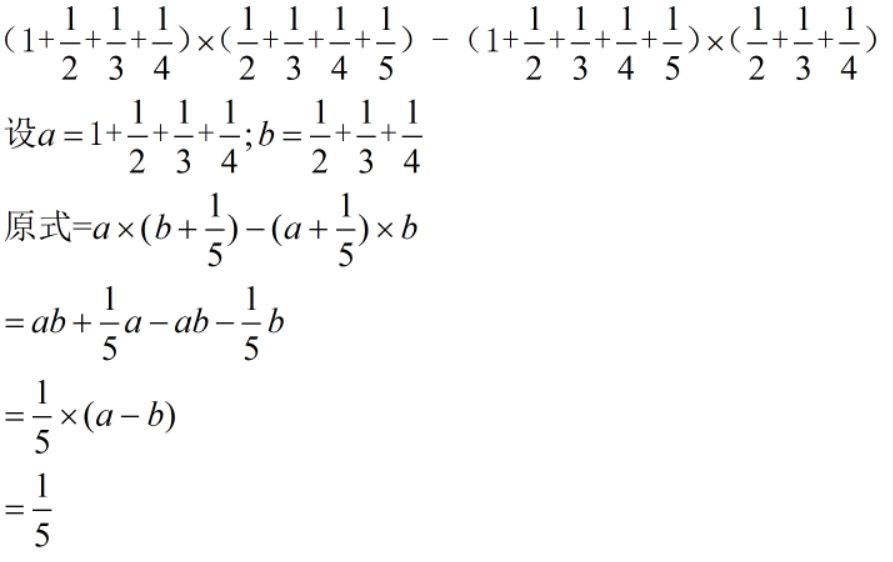
注：这里设未知数的方法很多，只给最方便计算的一类。
另：易错点，不是所有的题目a-b都是1，这个要真正计算才能代入。常见错误是默认为1.
————————————美丽的分割线————————————
哈哈，如果你还能坚持读到这里，那么先给你点一个大大的赞。这是截止到写稿子的时候，大梦老师脑海里浮现出的巧算方法，之后会一直更新的。
如果还喜欢我的文章，欢迎大家点一个关注哦~
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
