精雕软件怎么把图片转成灰度图_从高度图/纹理贴图生成法线贴图

高度图 -> 法线贴图

首先我们先回来考察一个平面它的法向量要怎么求，如果是一个数学狂人的话会开始写偏微分公式（？）不过这样看：

首先我有一个高度图, 然后对于图上（i，j）处的一点，我们可以知道它沿着S和T方向(把S和T想象成x和y）的两个向量是：

所以我们可以叉乘得到它的法向量：

哇撒，这也太简单了吧，来处理一张高度图：

我们读入tga,然后直接来处理：

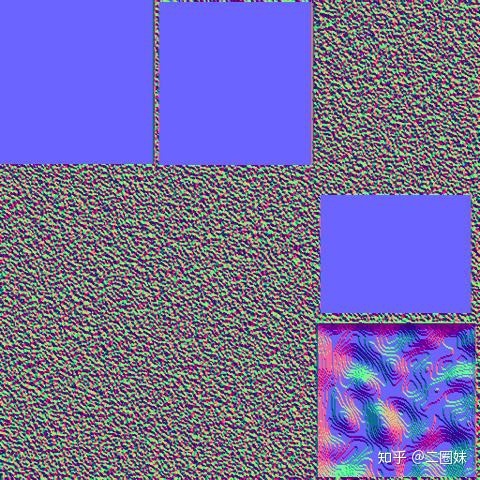
咦，跟想象的不太一样嘛，哦，原来忘记了乘以a，这个a选多大呢？

随机选个0.01吧，哇，looks good:

贴个对比图，这是附带的normal map:

基本跟附带的normal map一致了，欢欣鼓舞，至于这个0.01是哪来的，是神来之笔？？ ，其实是因为看到别人这么做的。。。然后选的0.01，我估计是跟sz和tz的范围相关，因为高度图，我们是用颜色来代表高度，而所有的高度在 0 - 255之间，这样减的差选0.01比较合适吧。

上面这个是情况特别简单的高度图。当我在互联网上尝试搜索‘复杂’一点点的同时带高度图和法线贴图的很难找到 ，然而同时看到了有很多用纹理图diffuse map转成灰度图grayscale map来模仿高度图的。

纹理图 -> 灰度图 -> 法线贴图

纹理图diffuse map，我们都知道是啥了，那么把它转成灰度图，就是r,g,b都是0-255之间的同一数值:

def graylize(r, g, b):
    return int(r * 0.2126 + g * 0.7152 + b * 0.0722)

至于为啥是这个组合，问就是俺也不知道（是对不同颜色的敏感性不同造成的）。。。换张复杂的图来检验算法：

转成灰度图：

转成normal map:

其实跟真实给出来的normal map 相差比较远：

感觉没有那么蓝绿感。丢失了一些细节。

看看别人是这么做的，用用别人的代码来看 -> 发现了一个程序: height2bump.py，用它来试试我的灰度图（这个文件是python2的，稍微改几行让它在Python3中运行）:

感觉把它用在灰度图上比我的效果还差，虽然这个算法还用了‘Sobel-Filter’优化，不过它用在高度图上应该比我的效果好一些（？）,但是找到的可用高度图测试就上面那一张，而且那一张感觉很简单 。

再看一次对比：

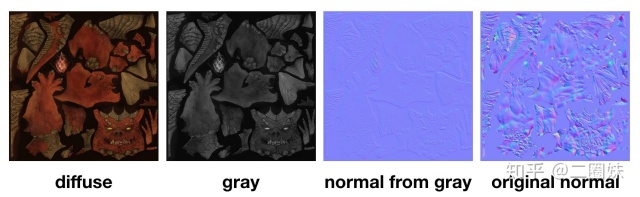
总结：

• 自带normal map最佳
• 高度图可以生成不错的normal map
• 没有高度图，纹理生成灰度图来模拟，但是这个得到的信息会有丢失

继续总结：

发现网上有算法，用四张照片来生成normal map.也是从四个不同的角度来打光，然后从照片中获得信息，最终生成normal map。

useful link:

• tutorial-13-normal-mapping: 文章下方也有一些资源，包括提到的一些错误，比如直接用diffuse来转normal.
• NormalMap-Online :在线转换工具，支持heightmap转normal或者四张照片生成normal
• The height2bump.py Program: 文中我提到的高度转normal，用了Sobel算子
• 根据纹理贴图生成法线图的算法, 如何改进? 感觉更像凹凸图 纹理贴图生成的法线图觉得改进空间不大，要么有足够的纹理贴图，否则它所包含的有高度/法向量的信息就是有限的