静电场与电流场_1.2.3 静电场、电场强度、静电场的叠加原理

现代的理论已经抛弃了荒谬的“超距作用”观点，转而采用场的观点来描述相互作用（这主要得益于法拉第的开创性贡献），并明确指出场也是与实物粒子具有同等地位的另一种物质存在形式。应用场的观点来解释库仑定律，不认为

是

受到的

直接施加的作用力，而是

处在

建立的电场中时受到的该电场施加的作用力。

由此，得出静电场的基本性质：静电场会对处于其中的电荷施加作用力。

一个静电场对于一个电荷施加的作用力称为电场力，这个作用力显然既与静电场有关也与这个电荷有关。而且正如上一节提到的，电荷的存在必然会对静电场本身造成一些影响。要在对静电场的定量化描述中完全忽略这样的影响，需要采取如下的办法：将给定的电荷

（称为试探电荷）放置在静电场存在区域内的某点

处，测量静电场对它施加的作用力

，显然

应当与电荷

和点

的位置矢量

都有关，记为

，而且该静电场必然受到

的影响。逐渐减小

的数值以便降低其对所研究的静电场的影响并继续测量作用力

，随着

的减小，比值

渐渐与

无关而只与

有关因而足以反映电场本身的性质，这一比值就

定义为该静电场在点

处的

电场强度

，在不致引起误解的情况下也直接称为电场

。相应的数学表述是：

把电场强度

的定义与真空中的库仑定律结合起来，就得到真空中的点电荷

在距该点电荷

处建立的电场

为：

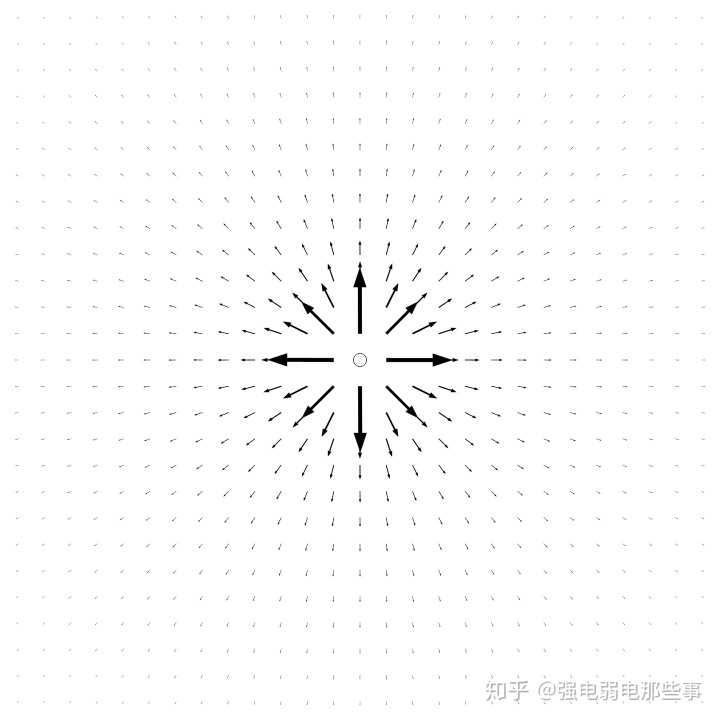
随

的分布如下图所示（以正点电荷为例），图中画出了空间中部分点处的电场强度矢量（点电荷位于图的中心，矢量的长度与电场强度的数值成正比）。这个电场具有明显的球对称性，距离点电荷越近，电场强度的数值就越大。

对于多个相对静止的点电荷

、

、…、

（各自的位矢分别为

、

、…、

）组成的体系在

处建立的静电场的电场强度

，依据电场强度定义并结合力的独立作用原理，立即得到

静电场的叠加原理：多个相对静止的点电荷组成的体系在某处建立的电场，等于这一体系内的每一个点电荷单独存在时在此处建立的电场的矢量和。用数学表述就是：

在上式中，

为待求电场分布的点（称为“场点”）的位矢，

为存在电荷分布的点（称为“源点”）的位矢，求和过程遍历电荷存在的区域。静电场的叠加原理从原则上已经解决了求解任意给定的静止点电荷体系所建立的电场的问题，在下一节中将运用该原理分析几种常见电荷体系的静电场，初步体会矢量和在计算上的复杂性。

当“场点”离“源点”很近即

的长度趋于0时，

的数值趋于无穷大，这显然是点电荷模型带来的问题。这一问题可以有两种解释：其一是在如此近的距离处必须考虑实际带电体的电荷分布情况因而不能再用点电荷模型；其二是在如此近的距离处，承载有电荷属性的微观粒子不能再视为几何点（也就是在这样的距离上库仑定律已经失效），经典电磁理论不再适用而必须用量子理论处理。两种解释都有一定的正确性，工程上一般采用前一种解释足以说明问题，但后一种解释更符合现代物理理论的观点。

根据实际电荷分布情况可以抽象出电荷的体分布、面分布和线分布模型。体分布指电荷分布在空间中的特定区域，用电荷体密度

（空间的单位体积内具有的电荷量）描述。面分布指电荷分布在曲面的特定区域，用电荷面密度

（曲面的单位面积上具有的电荷量）描述。线分布指电荷分布在曲线的特定区段，用电荷线密度

（曲线的单位长度上具有的电荷量）描述。由电场叠加原理可以得出这三种情况下求解电场分布的基本公式如下。

对于体分布：

对于面分布：

对于线分布：

这些公式的积分区域都遍及存在电荷分布的区域，并且只对“源点”的位矢

作积分，所得的积分式实际上是“场点”的位矢

的函数。

这里有一个问题：电荷是否受到它自己激发的电场的相互作用力？由于库仑定律的形式，这个问题在经典电磁理论范围内无法解释，需要使用量子理论来处理。在经典电磁理论范围内不能研究电荷与它自己激发的电场之间的相互作用。

要强调的是，场的观点指的是真实的，物理上存在的场，而不是抽象的数学上的场。数学上的场的意义，是在特定区域（例如最常见的三维空间中的某区域）上分布着的某种数、矢量、张量或是更复杂的量，例如温度场、速度场、应力场等等。物理上所说的场，不仅仅描述了某种物理量在空间中的分布及随时间的变化情况，更重要的是它与实物一样也是物质存在的基本形式之一。