 (本文适合初三)
“心似双丝网,中有千千结”,大千世界一定是由三角形织成,而三角形的内心、外心、重心、垂心及旁心是其千千结。这里要一眼看透的,其实是三角形的“内心”。
Q1:啥是三角形的内心啊?
当三角形与圆联系在一起,就会发生很多奇妙的事情。如果一个圆在三角形内部,并且这个圆与三条边恰好都相切,那么我们把这个圆叫做三角形的内切圆,它的圆心叫做三角形的内心。
(本文适合初三)
“心似双丝网,中有千千结”,大千世界一定是由三角形织成,而三角形的内心、外心、重心、垂心及旁心是其千千结。这里要一眼看透的,其实是三角形的“内心”。
Q1:啥是三角形的内心啊?
当三角形与圆联系在一起,就会发生很多奇妙的事情。如果一个圆在三角形内部,并且这个圆与三条边恰好都相切,那么我们把这个圆叫做三角形的内切圆,它的圆心叫做三角形的内心。

我们试图一眼看穿三角形的内心,有以下奇妙的结论:
(1)如上图,圆I是三角形△ABC的内切圆,I是三角形的内心,容易看出,I恰好是三条角平分线的交点。如果D、E、F分别是圆与边的切点,连结圆心和切点容易得到ID⊥AB,IE⊥BC,IF⊥CA,并且ID=IE=IF=r,是内切圆的半径。 (2)由于ID⊥AB,IE⊥BC,IF⊥CA,ID=IE=IF=r,因此我们可以把△ABC的面积拆成三个小三角形的面积之和:
我们看到三角形的面积可以表示为周长的一半与内切圆半径的乘积。
(3)对于给定的三角形,如果其面积为S,周长为C,那么我们很容易计算出其内切圆半径r= 2S/C。 Q2:内切弧 一片冰心在玉“弧”:如果我们放宽一点条件,对平面内给定的△ABC,如果存在一段弧与△ABC的两边相切(而不要求与三条边均相切),并且该弧大于等于一个半圆(即优弧),弧上所有的点都在△ABC的内部或边上,我们不妨称这样的弧为△ABC的“内切弧”。 从上图来看我们作了四个圆:圆O、圆P、圆I、圆Q都与△ABC的AB边和BC边相切,且圆心留在△ABC的内部或边上,都有超过了半圆的部分留在△ABC内,那我们可以叫留在三角形内的部分叫“内切弧”。
再例如下图的平面直角坐标系xOy中,若A(8,0),B(0,6),弧G2和弧G3与△ABC的两条边相切,半圆或优弧的所有点都在△ABC的内部,因此G2和弧G3就是△ABC的内切弧,但弧G1不是△ABC内的优弧,且只跟一条边相切,因此弧G1不是△ABC的内切弧。
从上图来看我们作了四个圆:圆O、圆P、圆I、圆Q都与△ABC的AB边和BC边相切,且圆心留在△ABC的内部或边上,都有超过了半圆的部分留在△ABC内,那我们可以叫留在三角形内的部分叫“内切弧”。
再例如下图的平面直角坐标系xOy中,若A(8,0),B(0,6),弧G2和弧G3与△ABC的两条边相切,半圆或优弧的所有点都在△ABC的内部,因此G2和弧G3就是△ABC的内切弧,但弧G1不是△ABC内的优弧,且只跟一条边相切,因此弧G1不是△ABC的内切弧。
 我们惊讶的发现:
(1)三角形的内切弧由于与两条边相切,因此内切弧的圆心也在三角形的角平分线上,而且从三条角平分线都可以作出内切弧,内切弧所在的圆有大有小,可谓“大珠小珠落玉盘”。
(2)经过探索,我们也很容易得出,内切弧的圆心必然落在三角形的内部(如果落在外部,那么留在三角形内的部分就小于半圆,不是优弧而是劣弧了)。
我们惊讶的发现:
(1)三角形的内切弧由于与两条边相切,因此内切弧的圆心也在三角形的角平分线上,而且从三条角平分线都可以作出内切弧,内切弧所在的圆有大有小,可谓“大珠小珠落玉盘”。
(2)经过探索,我们也很容易得出,内切弧的圆心必然落在三角形的内部(如果落在外部,那么留在三角形内的部分就小于半圆,不是优弧而是劣弧了)。

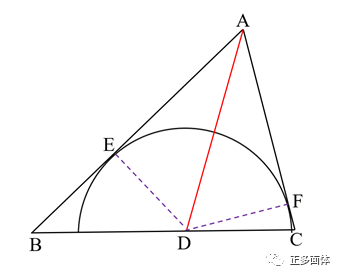 审视着上图,忽然有种豁然开朗的感觉:
(1)在上图中,完美内切弧的圆心,应该落在角平分线与三角形边的交点处,图中D向另两边作垂线,这样的半径才是最大的,如果D在角平分线AD的延长线上,那么落在形内的就不是优弧了,如果D沿DA向A移动,那么其半径明显是小于图中的DE的;
(2)经过内心性质的讨论,我们这里惊奇的发现,完美内切弧的半径与边长和三角形的面积有以下的关系:
审视着上图,忽然有种豁然开朗的感觉:
(1)在上图中,完美内切弧的圆心,应该落在角平分线与三角形边的交点处,图中D向另两边作垂线,这样的半径才是最大的,如果D在角平分线AD的延长线上,那么落在形内的就不是优弧了,如果D沿DA向A移动,那么其半径明显是小于图中的DE的;
(2)经过内心性质的讨论,我们这里惊奇的发现,完美内切弧的半径与边长和三角形的面积有以下的关系:


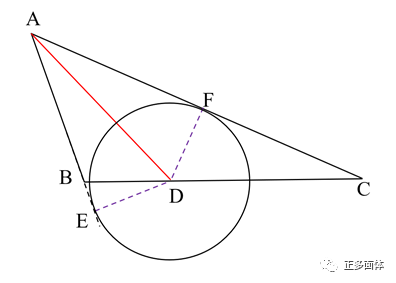
 而此时的半径PB BC > AB,因此完美内切弧的圆心应该在AC边上,这样我们前面讨论的结论仍然成立!
再例如,平面直角坐标系中,若A(8,0),B(0,6)
而此时的半径PB BC > AB,因此完美内切弧的圆心应该在AC边上,这样我们前面讨论的结论仍然成立!
再例如,平面直角坐标系中,若A(8,0),B(0,6)
 若弧G为△ABC的内切弧,且弧G与边AB、OB相切,那么弧G的半径的最大值为r= 2S/ (OB +AB) = 6×8/(6+10) = 3;
而若要求△ABC的完美内切弧,应该选取最短的两条边OA和OB,此时完美内切弧的半径为r= 2S / (OA+OB) =6×8/(6+8) = 24/7.
Q4:如此这般,如何是好?
问题进一步复杂,如果给一个动点M(m,3),连接OM、AM,那么△OAM的完美内切弧的半径的最大值是多少?
若弧G为△ABC的内切弧,且弧G与边AB、OB相切,那么弧G的半径的最大值为r= 2S/ (OB +AB) = 6×8/(6+10) = 3;
而若要求△ABC的完美内切弧,应该选取最短的两条边OA和OB,此时完美内切弧的半径为r= 2S / (OA+OB) =6×8/(6+8) = 24/7.
Q4:如此这般,如何是好?
问题进一步复杂,如果给一个动点M(m,3),连接OM、AM,那么△OAM的完美内切弧的半径的最大值是多少?



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








