函数的用法_Excel函数TREND函数的用法

TREND函数是一个线性趋势的预测函数，在已知Y值、X值的条件下，预测X对应的Y值：

TREND共有4个参数，三个必选参数，一个可选参数：

• 已知Y(必选)
• 已知X(必选)
• 新X(必选)
• 截距修正：TRUE:正常计算/FALSE:截距修正为1(可选)

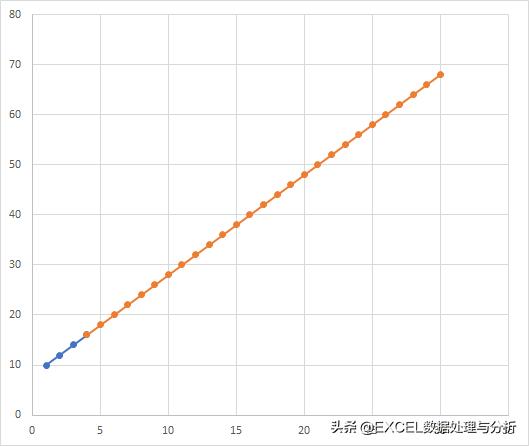
同样的一组数据第四参数不同，结果也是有区别的：

灰色曲线是由第四参数为FALSE时得到的结果生成的曲线。

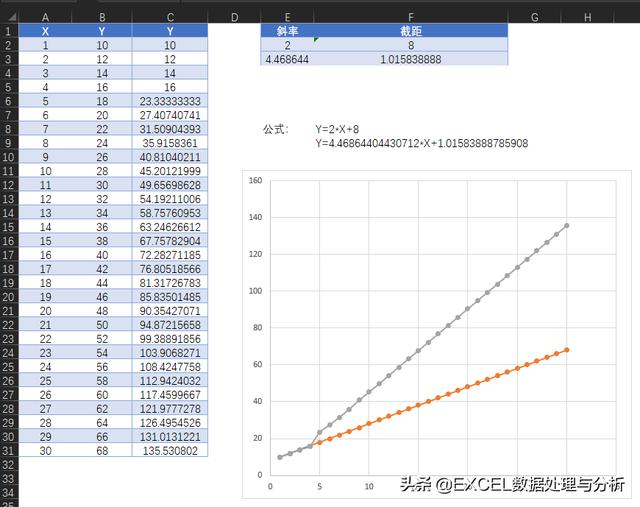
通过斜率与截距函数我们计算出这两条曲线的斜率与截距，可以看出，第四参数用FALSE就是将截距调整为1，然后做的计算。而第四参数用的TRUE或者省略，得到正常计算的截距是8。

第一与第二参数，要求每个参数至少提供两个已知值，第三参数是单个值。

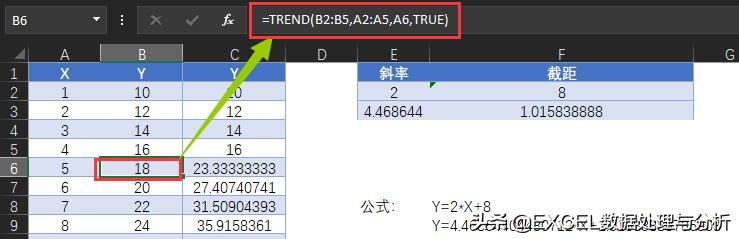
TREND函数可以用在已知历史数据，预测未来数据，当然数据符合线性规律，这个功能我们也可以用在编写绩效核算的公式中，我们举一个简单的例子：

例如：对于客户投诉的考核规定，在投诉数量小于或等于10次是为100分，每增加5次扣1分，直至扣完为止。

这是很常见的考核描述，如果给我们每个人的投诉数量，计算他们的得分，用TREND函数应该怎么来编写公式呢？

首先要找到已知值，然后来计算未知值：

• 已知Y1：100
• 已知X1：10

其实根据每增加5次扣1分，我们还可以得出最接近的一组已知条件：

• 已知Y2：99
• 已知X2：15

这样我们TREND函数的参数就凑齐了，还有一个第三参数，就是每个人的投诉量。

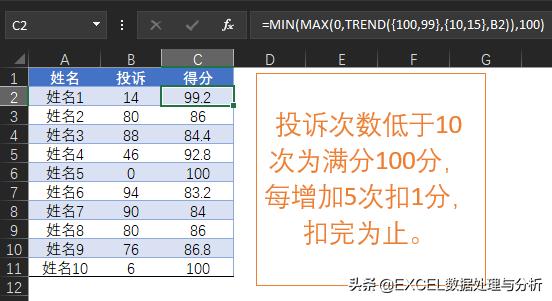
至于MIN、MAX函数的用法，就是为了设置最大与最小值。

如果需要了解MIN、MAX函数的用法，可以观看专栏视频：