怎么在java中实现树状数组_树状数组---原理代码实现

刚刚学了树状数组，有必要总结一下；

(因为有人说；别人能很快理解算法，最好是让刚刚理解的人来教而不是研究多年的大牛，因为刚刚理解的才知道初学的人哪里不会；；当然这也不一样啦~~~)

或许你还不知道什么是树状数组，这里大致讲一下(参考wiki，baidu)；

树状数组(BinaryIndexedTree，BIT，二分索引树)，最早由Peter

M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题，现多用于高效计算数列的前缀和。它可以以

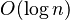的时间得到

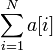，并同样以

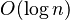对某项加一个常数。

用途：主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值。

与线段树的比较：这种数据结构(算法)并没有C++和Java的库支持，需要自己手动实现。在Competitive

Programming的竞赛中被广泛的使用。树状数组和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。相比较而言，树状数组效率要高很多。

看了这么多概念性的，相信你也烦了- -;不过这个确实需要了解；等你会了之后再看这个就一目了然为什么是如上面这样说的

我们常常需要某种特定的数据结构来使我们的算法更快，于是乎这篇文章诞生了。 在这篇文章中，我们将讨论一种有用的数据结构：数状数组(Binary Indexed Trees)。 按 Peter

M. Fenwich (链接是他的论文，TopCoder上的链接已坏)的说法，这种结构最早是用于数据压缩的。 现在它常常被用于存储频率及操作累积频率表。(都是废话，可以不用看了)

(重点操作)定义问题如下：我们有n个盒子，可能的操作为：

往第i个盒子增加石子(对应下文的update函数)

计算第k个盒子到第l个盒子的石子数量(包含第k个和第l个)

原始的解决方案中(即用普通的数组进行存储，box[i]存储第i个盒子装的石子数)， 操作1和操作2的时间复杂度分别是O(1)和O(n)。假如我们进行m次操作，最坏情况下， 即全为第2种操作，时间复杂度为O(n*m)。使用某些数据结构(如 RMQ)

，最坏情况下的时间复杂度仅为O(m log n)，比使用普通数组为快许多。 另一种方法是使用数状数组，它在最坏情况下的时间复杂度也为O(m log n)，但比起RMQ， 它更容易编程实现，并且所需内存空间更少。

BIT: 树状数组

MaxVal: 具有非0频率值的数组最大索引，其实就是问题规模或数组大小n

f[i]: 索引为i的频率值，即原始数组中第i个值。i=1…MaxVal

c[i]: 索引为i的累积频率值，c[i]=f[1]+f[2]+…+f[i]注意这些符号的含义待会讲的时候才不会乱当然我后面会不断说明其代表含义

tree[i]: 索引为i的BIT值(下文会介绍它的定义)

num^- : 整数num的补，即在num的二进制表示中，0换为1，1换成0。如：num=10101，则 num^- =01010

注意: 一般情况下，我们令f[0]=c[0]=tree[0]=0，所以各数组的索引都从１开始。 这样会给编程带来许多方便。

注意：这里累积频率你可以理解为前n项和

每个整数都能表示为一些2的幂次方的和，比如13，其二进制表示为1101，所以它能表示为： 13 = 20 + 22 +

23 .类似的，累积频率c[]可表示为其子集合之和。在本文的例子中， 每个子集合包含一些连续的频率值，各子集合间交集为空。比如累积频率c[13]= f[1]+f[2]+…+f[13]，可表示为三个子集合之和(这里说的三个是随便举例的， 下面的划分也是随便举例的)，c[13]=s1+s2+s3， 其中s1=f[1]+f[2]+…+f[4]，s2=f[5]+f[6]+…+f[12]，s3=f[13]。

idx记为BIT的索引，r记为idx的二进制表示中最右边的1后面0的个数(这个r后面还会出现记得它的含义)，

比如idx=1100(即十进制的12)，那么r=2。tree[idx]记为f数组中，

索引从(idx-2r+1)到idx的所有数的和，包含f[idx-2r+1]和f[idx]。即：tree[idx]=f[idx-2r+1]+…+f[idx]，对照表1.1和1.2理解和推算一下，你就会一目了然。 我们也可称idx对索引(idx-2r+1)到索引idx负责(比如表1.2的

8管着1-8,9管着9)。(We also write that idx is responsible for indexes from (idx-2r+1)to idx)

()

假设我们要得到索引为13的累积频率(即c[13])，在二进制表示中，13=1101。因此(你看一下上面那个图)， 我们是不是可以这样计算：c[1101]=tree[1101]+tree[1100]+tree[1000]  (c[13]=tree[13](管着f[13])+tree[12](管着f[9]~f[12])+tree[8](管着f[1]~f[8]))，后面将详细讲解。

你先观察上面这个式子c[1101]=tree[1101]+tree[1100]+tree[1000]    有没有发现tree[ ]有上面规律？

这里先给出上面那个问题的规律；每次分离出最后的一 不知道聪明的你有么有发现

注意: 最后的1表示一个整数的二进制表示中，从左向右数最后的那个1。

由于我们经常需要将一个二进制数的最后的1提取出来，因此采用一种高效的方式来做这件 事是十分有必要的。令num是我们要操作的整数。在二进制表示中，num可以记为a1b  (比如什么 101101(a) 1(1) 1001(b)这个是废话其实可以不用看), a代表最后的1前面的二进制数码，由于a1b中的1代表的是从左向右的最后一个1，

因此b全为0，当然b也可以不存在。比如说13=1101，这里最后的1右边没有0，所以b不存在。(都是废话)

我们知道，对一个数取负等价于对该数的二进制表示取反加1。

所以-num等于(a1b)^- +1= a^- 0b^- +1。由于b全是0，所以b^- 全为1。最后，我们得到：

-num=(a1b)^- +1=a^- 0b^- +1=a^- 0(1…1)+1=a^- 1(0…0)=a^- 1b

现在，我们可以通过与操作(在C++,java中符号为&)将num中最后的1分离出来：

num & -num = a1b & a^- 1b = (0…0)1(0…0)

这里给出一个函数：

int lowbit(int x)

{

return x&(-x);

}(还记得刚刚那个r吗(r为idx的二进制表示中最右边的1后面0的个数))两者其实是一样的

即 lowbit(i) ==2^r

给定索引idx，如果我们想获取累积频率即c[idx]，我们只需初始化sum=0, 然后当idx>0时，重复以下操作