图形大小_生态数学空中课堂（一）平面图形复习-CSDN博客

本文链接：https://blog.csdn.net/weixin_30069591/article/details/112655787

平面图形的认识(一)

——人教版六年级下册第六单元《图形与几何》

生态数学工作室李继红

过程：

1.同学们大家好！这节课我们来整理和复习图形的认识与测量一

首先我们来一起来回忆一下，我们学过哪些平面图形和立体图形？你能对学过的图形进行分类吗？

下面大家用自己的方法来总结我们学过的平面图形和立体图形吧。时间2分钟。

下面我们来看一看同学们总结的知识点吧。

(出示学生的作品)

2.那我们学过的平面图形哪些呢？你能说说吗？

我们学过的图形分为平面图形和立体图形。平面图形中我们学过三角形、四边形、圆，立体图形我们学过长方体正方体，圆柱和圆锥。

三角形可以按边分，也可以按角来分。按边分可以分为一般三角形和等腰三角形，在等腰三角形中还有3边都相等的等边三角形。按角分可以分为锐角三角形，钝角三角形，直角三角形。

四边形可以分为一般四边形，梯形和平行四边形。梯形有两种特殊的梯形：直角梯形和等腰梯形。平行四边形中特殊的是长方形，长方形中特殊的是正方形。

立体图形中我们学过了长方体，长方体中特殊的是正方体。还有圆柱和圆锥。

4.这是我们在小学阶段学过的平面图形和立体图形。

逐步出示以下PPT：

5.下面我们对组成平面图形的基本要素进行梳理。我们学过直线，射线和线段。它们有什么联系和区别呢？除此之外，同一平面内两条直线有哪几种位置关系呢？下面大家通过这个表格进行整理和复习。

首先我们来看直线。直线有什么特点呢？直线没有端点，可以两端无限延长，因此无法度量；射线只有一个端点，另一端可以无限延长，因此无法度量；线段有直线里的一个部分，有两个端点，因此可以度量；

我们再来看两条线之间的关系。在同一平面内，有两种位置关系，相交和平行。当两条直线相交成直角时就是互相垂直；在同一平面内当两条直线永远不相交的时候，我们就说这两条直线互相平行。(位置关系是不是相交和平行，其中相交中比较特殊的是相交成直角，就是垂直？)

逐步出示以下表格：

6.下面我们来复习一下，我们学过哪些角呢？我们来通过这个表格来进行整理。想一想每个角的图示是怎样的？它们的度数范围是怎样的？

我们先来说说锐角。锐角都是大于0度而小于90度的，直角通常用直角符号来标注，直角是90度。钝角是这个样子的，都是大于90度小于180度，平角就像一条直线，中间有一个角是平角的顶点(中间有一个点是平角的顶点)，平角都是180度。平角里有几个直角呢？是的有两个直角。周角长成这个样子，周角有360度。

大家想一想，在放大镜下看角，它的大小会变化吗？

对，角的两边是射线，可以无限延长，角的大小取决于两条射线叉开的大小，因此用放大镜看角，不会改变两条射线叉开的大小，是不会改变角的大小。

7.下面我们梳理一下有关三角形的知识。有关三角形，你都知道些什么呢？

下面是一个三角形，我们知道三角形有三条边，三个角和三个顶点。由3条线段首尾相连围成的图形叫三角形。从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高。这条对边叫三角形的底。想一想，一个三角形有几条高呢？大家知道，三角形有三个顶点，每个顶点都可以向它的对边作垂线，因此一个三角形有三条高。

我们可以根据三角形的特征对三角形进行分类。既可以按边分，也可以按角分。

我们可以借助集合圈的方式，将各类三角形之间的关系表达得更清晰。

如按边分：普通的三角形中有两条边相等的三角形，也叫等腰三角形，相等的两条边就是三角形的腰，在等腰三角形中更特殊的有三条边相等的三角形(也叫等边三角形)，

按角边：如果三角形的三个角都是锐角，这个三角形就是锐角三角形；如果有一个角是直角，这个三角形就是直角三角形；如果有一个角是钝角，这个三角形就是钝角三角形；这三类三角形不会交叉，是并列关系。

关于三角形，我们还研究过它的内角，无论是哪一种三角形，它的内角和都是180°，除此之外，我们还研究过三角形三条边长度之间的关系。在一个三角形中，任意两边之和都大于第三边。

8.下面我们来根据三角形的知识来解决一下下面的问题吧。

第一个三角形：因为三角形的内角和是180度，所以第三个角的度数是180°-70°-40°=70度。我们可以知道在这个三角形中有两个角的度数都是70度，这个三角形就是等腰三角形，这两个角称为等腰三角形的底角，40度的这个角称为等腰三角形的顶角。

第二个三角形是个直角三角形，其中有一个角是直角，因此，其余两个角的和是90度，要求的角是90°-55°=35°。

最后一个三角形是一个钝角三角形。我们可以先求出红色钝角的度数：180°-40°=140度。然后再用180°-15°-140°=25度。

9.下面我们来动动脑筋思考一下下面这道题

一个三角形的三个内角互不相等，最小的内角是45度。这个三角形按角分类属于()三角形。

我们来分析一下，因为三个内角互不相等，假设三个角分别是角1最小，角2次之，角3最大，因为题目中说最小的内角是45度，那么角1就是45度了，可知第二大的角2一定大于45度，那么角1+角2的和一定大于90度，因为三角形三个内角之和是180度，所以角3一定小于90度。这样看来，三个角都是锐角，所以这个三角形是锐角三角形。

下面我们来看一看下面有长度为3厘米，4厘米，5厘米，6厘米的小棒各一根，哪三根小棒可以围成一个三角形？

10、下面我们来复习平行四边形的知识。关于平行四边形，你知道些什么？

平行四边形的对边互相平行，而且对边也相等。我们称两组对边分别平行的四边形叫做平行四边形。从平行四边形的一条边上的一个点向对边引一条垂线，这点和垂足之间的线段叫做平行四边形的高，垂足所在的边叫做平行四边形的底。

我们可以用集合圈来表示平行四边形、长方形和正方形之间的关系。(感觉衔接)长方形是特殊的平行四边形，特殊就特殊在长方形的四个角都是直角。而正方形是特殊的长方形，特殊在正方形的四条边都相等。因此我们说正方形是特殊的长方形，长方形是特殊的平行四边形。

11.下面我们来复习有关梯形的知识。只有一组对边平行的四边形，叫做梯形。梯形中也有特殊的梯形。两腰相等的梯形叫做等腰梯形，有一个角是直角的梯形叫做直角梯形。

刚才我们复习的各种四边形的特征，我们可以用这样的一个集合圈来表示各种四边形的关系。

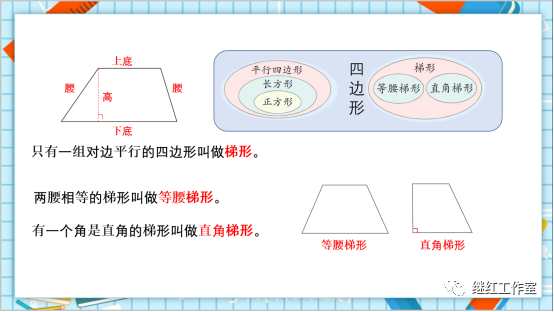
从这个图中我们可以看出最大的圈代表着四边形大家庭。这个大家族中有两类比较特殊的四边形，一类是平行四边形家族，另一类是梯形家族。平行四边形中比较特殊的是长方形，长方形中比较特殊的是正方形，而梯形中有两类并列的特殊梯形，一类是等腰梯形，一类是直角梯形。

12.下面我们来做一个选择，将一个长方形框架拉成一个平行四边形，与长方形相比，什么变了，什么没变呢？请大家自己读题进行选择。我们来看一看，当把一个长方形的框架拉成一个平行四边形的时候，这个长方形的四条边的长度发生变化了吗？的确，它们的长度并没有发生变化，只是边与边之间的位置关系发生了变化。因此将长方形拉成平行四边形的过程，周长没有发生变化。面积呢？我们来看这是长方形的面积，这是平行四边形的面积。由于平行四边形的面积等于底乘高，从图中我们明显可以看到平行四边形的高小于长方形的宽，因此在拉动的过程中，面积是变化的。所以在四个选项中，只有C选项是正确的。周长不变，面积变了，而且是变小了，因为拉动的过程中高越来越小了。

13.最后，我们来复习有关圆的知识。

现在同学们看到的是用圆规画出的一个圆。用圆规画圆时，针尖所在的点叫圆心，一般用字母O表示，连结圆心到圆上任意一点的线段叫半径，一般用字母r表示，半径的长度就是圆规两个脚之间的距离。通过圆心并且两端都在圆上的线段叫做直径，一般用字母d表示。我们都知道，在同一个圆里，直径是半径的2倍，半径是直径的1/2。其实，对于一个圆来说，最核心的要素是圆心和半径。圆心决定了圆的位置，半径决定了圆的大小。我国古代的《墨经》中简明扼要地提出：圆，一中同长也。这里的一中就是确定圆位置的圆心，而同长则是指圆中无数条的半径都相等。