三角形一点到三边距离最小_姜姜老师：（补充）几何最值模型——施瓦尔兹三角形...

故事背景：

德国数学家施瓦尔兹(1843—1921)第一个用完全初等的方法对下面命题给出了一个漂亮的证明。在锐角三角形 ABC 中，若 D、E、F 分别是三条高 AD、BE、CF 的垂足，则在三角形 ABC 的所有内接三角形中，以垂足为顶点的三角形 DEF 的周长最短。

模型证明

在锐角三角形中，D，E，F分别为三边上的动点，三角形DEF周长最小值如何求解？

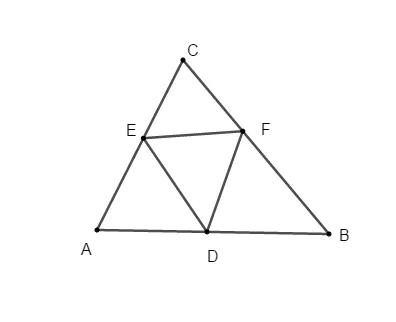
1、可以利用线段和差最值中角内一定两动来处理，把D点当作定点来处理，先求定点D下的三角形DEF周长最小。

2、分别做D关于线段AB与AC的对称点；D`和D`1此时D`D`1为周长最小值

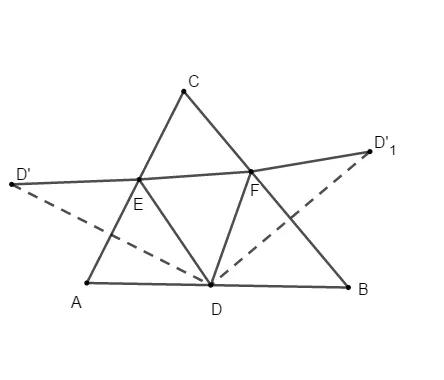
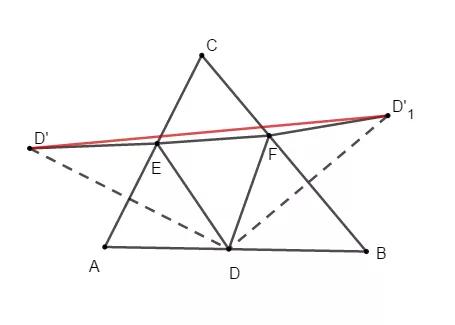
3、连接CD`与CD`1 ，由对称的性质可以得出三角形CD`D`11为等腰三角形，且∠D`CD`1 为∠ACB的2倍，所以三角形CD`D`1 形状固定三角形，当CD`最小时周长最小，即CD最小;

4、连接CD`与CD`1，由对称的性质可以得出三角形CD`D`1为等腰三角形，且∠ D`CD`1为∠ACB的2倍，所以三角形CD`D`1形状固定三角形，当CD`最小时周长最小，即CD最小;

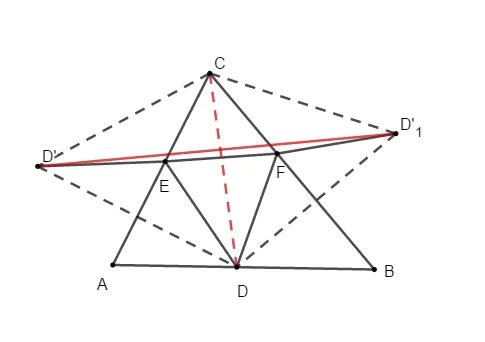
5、 当CD⊥AB时，CD最小。

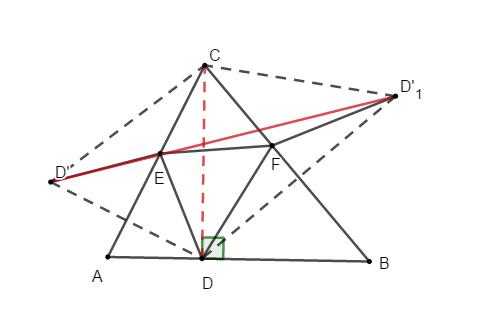
6、连接BE与AF，若把F，E分别当作定点构造可得垂直时E，F为也为垂足时满足，所以最小值为三垂足连线。

模型练习

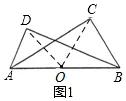
1．如图，点D是△ABC中AB边上的一个动点，点D关于AC，BC对称点分别是点E和点F，∠A＝45°，∠B＝75°，AC＝8，则EF的最小值是(　　)

A．4 B．8 C．4 D．4

2．

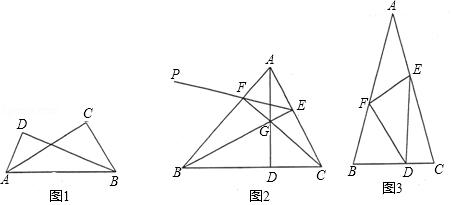
(1)如图l，Rt△ABD和Rt△ABC的斜边为AB，直角顶点D、C在AB的同侧，求证：A、B、C、D四个点在同一个圆上．

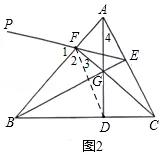
(2)如图2，△ABC为锐角三角形，AD⊥BC于点D，CF⊥AB于点F，AD与CF交于点G，连结BG并延长交AC于点E，作点D关于AB的对称点P，连结PF．求证：点P、F、E三点在一条直线上．

(3)如图3，△ABC中，∠A＝30°，AB＝AC＝2，点D、E、F分别为BC、CA、AB边上任意一点，△DEF的周长有最小值，请你直接写出这个最小

【解答】

解：(1)如图1，取AB的中点O，连结OD，OC，

∵Rt△ABD和Rt△ABC的斜边为AB，

∴OD＝½AB，OC＝½AB，

∴OA＝OB＝OC＝OD，

∴A、B、C、D四个点在同一个圆上．

(2)如图2，连结DF，

∵点D、P关于AB对称，

∴∠1＝∠2，

∵AD⊥BC于点D，CF⊥AB于点F，

∴∠2+∠3＝90°，∠4+∠BCE＝90°，BE⊥AC，点A、C、D、F四点共圆，

∴点B、F、E、C四点共圆，∠3＝∠4，

∴∠2＝∠BCE，∠BFE+∠BCE＝180°，

∴∠2+∠BFE＝180°，

∴∠1+∠BFE＝180°，

∴点P、F、E三点在一条直线上．

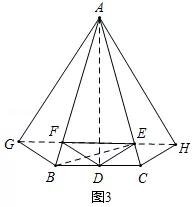
(3)如图3，作点D关于AB的对称点G，作点D关于AC的对称点H，连接GF，HE，则DF＝GF，DE＝HE，

∴当点G，F，E，H在同一直线上时，GF+FE+EH＝GH(最短)，

此时，DF+FE+DE最短，即△DEF的周长有最小值，

由轴对称的性质，可得∠GAH＝2∠BAC＝60°，AG＝AD＝AH，

∴△AGH是等边三角形，

∴△DEF的周长最小值＝GH＝AD，

∵当AD⊥BC时，AD有最小值，

∴当AD⊥BC时，△DEF的周长有最小值，

连接BE，

---

温馨提示

“知识“无价，老师作为“知识“的传播者，有责任和义务让更多同学提升自己，也是我的初衷。初中数学压轴公众号除了中考数学必备题型、知识点、特殊题型内容的讲解，还有一些关于亲子教育、家庭教育等内容。学习和教育是相辅相成的，学习文化知识只是人生历程的一部分而已，个人教育更是贯穿人的一生。

———姜姜老师

希望本文对你有所帮助，请持续关注后续更新的精彩内容！

欢迎私信留言，领取“中考知识考点资料大礼包”

更多精彩······

姜姜老师：初中数学几何最值“降龙十八掌”合集——1-6讲

姜姜老师：初中几何最值研究模型合集“降龙十八掌”——7-12讲

中考典型题型：初中几何最值模型17——“胡不归”

「中考考点」姜姜老师讲解：初中几何最值模型18——“阿氏圆”