BZOJ 2648/2716(SJY把件-KD_Tree)[Template:KD_Tree]

2648: SJY把件

Time Limit: 20 Sec   Memory Limit: 128 MB
Submit: 1180   Solved: 391
[ Submit][ Status][ Discuss]

Description

这天，SJY显得无聊。在家自己玩。在一个棋盘上，有N个黑色棋子。他每次要么放到棋盘上一个黑色棋子，要么放上一个白色棋子，假设是白色棋子。他会找出距离这个白色棋子近期的黑色棋子。此处的距离是 曼哈顿距离 即(|x1-x2|+|y1-y2|) 。如今给出N<=500000个初始棋子。

和M<=500000个操作。

对于每一个白色棋子，输出距离这个白色棋子近期的黑色棋子的距离。同一个格子可能有多个棋子。

 

Input

第一行两个数 N M

以后M行。每行3个数 t x y

假设t=1 那么放下一个黑色棋子

假设t=2 那么放下一个白色棋子

Output

对于每一个T=2 输出一个最小距离

 

Sample Input

2 3
1 1
2 3
2 1 2
1 3 3
2 4 2

Sample Output

1
2

HINT

 

kdtree能够过

Source

鸣谢 孙嘉裕

提示中已有kd-tree了，那么百度一下

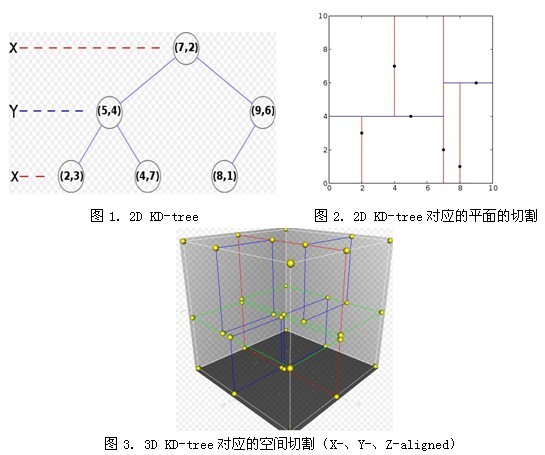
考虑平面上一堆点，先找出横坐标中位数的点。取出。对着切一刀，剩下点分为2半

然后对当中一边竖着切，再横着切。。。。

转自：http://www.cnblogs.com/slysky/archive/2011/11/08/2241247.html

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])  
#define Lson (x<<1)
#define Rson ((x<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (1000000000)
#define F (100000007)
#define MAXN (500000+10)
#define MAXM (500000+10)
typedef long long ll;
ll mul(ll a,ll b){return (a*b)%F;}
ll add(ll a,ll b){return (a+b)%F;}
ll sub(ll a,ll b){return (a-b+(a-b)/F*F+F)%F;}
void upd(ll &a,ll b){a=(a%F+b%F)%F;}
int n,m;

int cmp_d=0;
class node
{
public:
	int x[2];
	int l,r,minv[2],maxv[2];

	node(){}
	node(int a,int b){MEM(x) l=r=0; x[0]=a,x[1]=b; Rep(i,2) minv[i]=maxv[i]=x[i];}



	int& operator[](int i){return x[i];	} 
};

int dis(node a,node b){
	int ans=0;
	Rep(i,2) ans+=abs(a.x[i]-b.x[i]);
	return ans;	
}

int dis2(node p,node a) // 点p和方形区域a的欧几里德距离 
{
	int ans=0;
	Rep(i,2)
	{
		if (p.x[i]<a.minv[i]) ans+=a.minv[i]-p.x[i];
		else
		if (p.x[i]>a.maxv[i]) ans+=p.x[i]-a.maxv[i];
	}
	return ans;
}


int cmp(node a,node b){return a[cmp_d]<b[cmp_d];	}

class KD_Tree
{
public:	
	node a[MAXN*3];

	KD_Tree()
	{ 	
	}
	
	void mem()
	{
	}
	
	void update(node& o)
	{
		if (o.l)
		{
			node p=a[o.l];
			Rep(i,2) o.minv[i]=min(o.minv[i],p.minv[i]);
			Rep(i,2) o.maxv[i]=max(o.maxv[i],p.maxv[i]);	
		}
		if (o.r)
		{
			node p=a[o.r];
			Rep(i,2) o.minv[i]=min(o.minv[i],p.minv[i]);
			Rep(i,2) o.maxv[i]=max(o.maxv[i],p.maxv[i]);	
		}
		
	}

	int build(int L,int R,int nowd)
	{
		int m=(L+R)>>1;
	
		cmp_d=nowd;
		nth_element(a+L+1,a+m+1,a+R+1,cmp);
		
		if (L^m) a[m].l=build(L,m-1,nowd^1);
		if (R^m) a[m].r=build(m+1,R,nowd^1);
		
		update(a[m]);
		
		return m;
		
	} 
	
	int root;
	void _build(int L,int R,int nowd)
	{
		root=build(L,R,nowd);
	}
	
	void insert(int o,int k,int nowd)
	{
		int p=a[o].x[nowd];
		int p2=a[k].x[nowd];
		
		if (p2<=p) 
		{
			if (a[o].l) 
				insert(a[o].l,k,nowd^1);
			else a[o].l=k;
		}
		else
		{
			if (a[o].r)
				insert(a[o].r,k,nowd^1);		
			else a[o].r=k;
				
		}
		
			
		update(a[o]);	
			
	}
	void _insert(int k,int nowd)
	{
		int p=root;
		insert(root,k,nowd);		
	}
	
	
	node _p;
	int _ans;
	
	void ask_min_dis(int o)
	{
		if (o==0) return;
		_ans=min(_ans,dis(a[o],_p));
		
		int ans1=a[o].l ?

dis2(_p,a[a[o].l]) : INF; // 点p到区域内随意一点的距离的最小值 int ans2=a[o].r ? dis2(_p,a[a[o].r]) : INF; if (ans1<ans2) { if(ans1<_ans) ask_min_dis(a[o].l); if(ans2<_ans) ask_min_dis(a[o].r); } else { if(ans2<_ans) ask_min_dis(a[o].r); if(ans1<_ans) ask_min_dis(a[o].l); } } int _ask(node p) { _p=p;_ans=INF; ask_min_dis(root); return _ans; } }S; int main() { // freopen("bzoj2648.in","r",stdin); // freopen("bzoj2648.out","w",stdout); cin>>n>>m; For(i,n) { int x,y; scanf("%d%d",&x,&y); S.a[i]=node(x,y); } S.a[++n]=node(INF,INF); S._build(1,n,0); For(i,m) { int p,x,y; scanf("%d%d%d",&p,&x,&y); if (p==1) { S.a[++n]=node(x,y); S._insert(n,0); } else { printf("%d\n",S._ask(node(x,y))); } } return 0; }

版权声明：本文博主原创文章。博客，未经同意不得转载。

转载于:https://www.cnblogs.com/hrhguanli/p/4850706.html