这里的 a0 是某个整数而所有其他的数 an 都是正整数。可依样定义出更长的表达式。如果部分分子(partial numerator)和部分分母(partial denominator)允许假定任意的值,在某些上下文中可以包含函数,则最终的表达式是广义连分数。在需要把上述标准形式与广义连分数相区别的时候,可称它为简单或正规连分数,或称为是规范形式的。
连分数常用于无理数的逼近,例如:
 由此得到
由此得到 的渐近分数
的渐近分数  、
、 、
、 、
、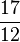 、……
、……
考虑实数 r。设 i 是 r 的整数部分,而 f 是它的小数部分。则 r 的连分数表示是 [i; …],这里的“…”是 1/f 的连分数表示。习惯上用分号取代第一个逗号。
要计算实数 r 的连分数表示,写下 r 的整数部分(技术上 floor)。从 r 减去这个整数部分。如果差为 0 则停止;否则找到这个差的倒数并重复。这个过程将终止,当且仅当 r 是有理数。
| 找出 3.245 的连分数 | ||||
|---|---|---|---|---|
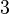 |  |  |  |  |
 | 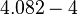 |  |  |  |
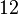 |  |  |  | 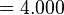 |
 |  | 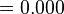 | STOP | |
| 3.245 的连分数是 [3; 4, 12, 4] | ||||
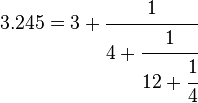 | ||||
数 3.245 还可以表示为连分数展开 [3; 4, 12, 3, 1];参见下面的有限连分数。
这个算法适合于实数,但如果用浮点数实现的话,可能导致数值灾难。作为替代,任何浮点数是一个精确的有理数(在现代计算机上分母通常是 2 的幂,在电子计算器上通常是 10 的幂),所以欧几里德GCD算法的变体可以用来给出精确的结果。
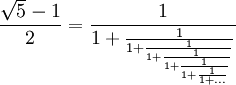 由此得到黄金分割的渐近分数
由此得到黄金分割的渐近分数  、
、 、
、 、
、 、
、 、
、 、……
、……
- 注意将上述系列的分子分母依序排列均可得到 斐波那契数列。
数学上可以证明,由(狭义)连分数得到的渐近分数,在分子或分母小于下一个渐进分数的分数中,其值是最接近精确值的近似值。
研究连分数的动机源于想要有实数在“数学上纯粹”的表示。
多数人熟悉实数的小数表示:
这里的 a0 可以是任意整数,其它 ai 都是 {0, 1, 2, ..., 9} 的一个元素。在这种表示中,例如数 π 被表示为整数序列 {3, 1, 4, 1, 5, 9, 2, ...}。
这种小数表示有些问题。例如,在这种情况下使用常数 10 是因为我们使用了 10 进制系统。我们还可以使用 8 进制或 2 进制系统。另一个问题是很多有理数在这个系统内缺乏有限表示。例如,数 1/3 被表示为无限序列 {0, 3, 3, 3, 3, ....}。
连分数表示法是避免了实数表示的这两个问题。让我们考虑如何描述一个数如 415/93,约为 4.4624。近似为 4,而实际上比 4 多一点,约为 4 + 1/2。但是在分母中的 2 是不准确的;更准确的分母是比 2 多一点,约为 2 + 1/6,所以 415/93 近似为 4 + 1/(2 + 1/6)。但是在分母中的 6 是不准确的;更准确分母是比 6 多一点,实际是 6+1/7。所以 415/93 实际上是 4+1/(2+1/(6+1/7))。这样才准确。
去掉表达式 4 + 1/(2 + 1/(6 + 1/7)) 中的冗余部分可得到简略记号 [4; 2, 6, 7]。
实数的连分数表示可以用这种方式定义。它有一些可取的性质:
- 一个数的连分数表示是有限的,当且仅当这个数是有理数。
- “简单”有理数的连分数表示是简短的。
- 任何有理数的连分数表示是唯一的,如果它没有尾随的 1。(但是 [a0; a1, ... an, 1] = [a0; a1, ... an + 1]。)
- 无理数的连分数表示是唯一的。
- 连分数的项将会重复,当且仅当它是一个二次无理数(即整数系数的二次方程的实数解)的连分数表示 [1]。
- 数 x 的截断连分数表示很早产生 x 的在特定意义上“最佳可能”的有理数逼近(参阅下述定理 5 推论 1)。
最后一个性质非常重要,且传统的小数点表示就不能如此。数的截断小数表示产生这个数的有理数逼近,但通常不是非常好的逼近。例如,截断 1/7 = 0.142857... 在各种位置上产生逼近比,如 142/1000、14/100 和 1/10。但是明显的最佳有理数逼近是“1/7”自身。π 的截断小数表示产生逼近比,如 31415/10000 和 314/100。π 的连分数表示开始于 [3; 7, 15, 1, 292, ...]。截断这个表示产生极佳的有理数逼近 3、22/7、333/106、355/113、103993/33102、...。 314/100 和 333/106 的分母相当接近,但近似值 314/100 的误差是远高于 333/106 的 19 倍。作为对π的逼近,[3; 7, 15, 1] 比 3.1416 精确 100 倍。
現在我們先回想一下歐幾里德計算法:
設 a,b 為兩整數,且 b>a,則

這個計算法是在紀元前三世紀時由歐幾里德發現的,記載在他不朽的《原本》裡第七卷上。它的主要目的在於求兩數 a 與 b 的最大公因數(即上式中之 rN)。今天,如果我們要電子計算機為我們設計解決最大公因數的問題的話,我們該為歐幾里德驕傲,因為他兩千年前用的這個方法仍然是目前最棒的。
現在,我們把(甲)組裡的式子全寫為分式,如下所示:

再將乙組中第一式之 ![]() 以第三式之倒數代入,接著
以第三式之倒數代入,接著 ![]() 以第三式之倒數代入,依次類推,即得
以第三式之倒數代入,依次類推,即得

上式之右邊即所謂的「連分數」(更精確地說,有窮簡單連分數)。為了節省篇幅及簡便起見,我們簡寫為
以下是连分数代码的实现 纯属本人按图索骥 如有不足请指出
#include < cmath >
using namespace std;
__int64 Num[ 1000 ]; // 记录连分数数列
// Continued fractions
long Fraction(__int64 r,__int64 f)
{
__int64 m = 1 ;
while (m <= f)
{
m *= 10 ;
}
__int64 s = r * m + f;
long len = 0 ;
while (s % m != 0 )
{
__int64 t = s % m;
Num[len ++ ] = s / m;
s = m;
m = t;
}
Num[len ++ ] = s / m;
// 将分母依次存入数列
return len;
}
int main()
{
__int64 r,f;
while (scanf( " %I64d.%I64d " , & r, & f) != EOF)
{
long len = Fraction(r,f);
long i;
for (i = 0 ;i < len; ++ i)
{
printf( " %ld:%I64d\n " ,i + 1 ,Num[i]);
}
}
return 0 ;
}








 由此得到
由此得到 、
、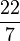 (
(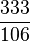 、
、 (
(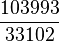 、……
、……














 2187
2187

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








