反演魔术:反演原理及二项式反演

反演过程就是利用  来表示出
来表示出 

这样的话,我们只需要知道 的求解方法和
的求解方法和 和
和 的关系,就可以快速求解
的关系,就可以快速求解
本质上来说,反演其实是一个解线性方程组的过程,但是你观察后发现,这个矩阵实际上是一个三角矩阵,那必然存在着快捷的方法。对于使得这两个反演公式成立的这些系数应该满足什么条件呢?我们现在就来探讨一番!
我们首先讨论一下在什么情况下能够比较容易建立反演公式,之后介绍二项式反演以及它的两个应用,其中一个是错位排列问题
反演原理
首先我来介绍一个  函数,这个函数被称为 Kronecker's delta,它是这样定义的
函数,这个函数被称为 Kronecker's delta,它是这样定义的

这个函数的定义非常简单,我介绍它完全是为了后面叙述的方便
好,我们现在来考虑一下上面的式子,假设对于任意  都满足
都满足

那么我们来考虑一下下面这个式子成立应该要满足什么条件
 $(1)$
$(1)$
我们可以直接将  代入上式来计算左边的求和
代入上式来计算左边的求和

对于最后一步,实际上是变换了求和顺序,为了更容易理解,我按照矩阵的形式写出来
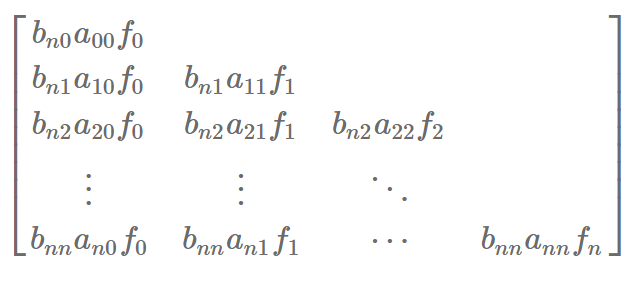
那么,前一个求和是先对行进行,再将各行加起来,后一个就是先对列进行,再将各列加起来
这样的话,等式$1$成立的充要条件就是

同样地,我们反过来也能知道,整个反演公式要成立还需要满足一个必要条件

也就是,如果你发现某个数列满足上面这个条件,那么你就可以直接建立起反演公式!
事实上,在快速傅立叶变换和逆变换你也可以认为是一个反演的过程,具体可以看这一步的推导,你会发现它和这个很相似。此外,第一类 Stirling 数和第二类 Stirling 数也满足这个条件,不过我暂时没有发现它们建立起的反演公式有什么应用。我下面来介绍一个比较有用的反演公式
二项式反演
下面就来介绍二项式反演(binomial inversion),这可以表示成

你会发现这个式子具有极强的对称性!另外一个更加常见的形式是

现在我们先来给出这个公式的一个容斥解释,之后从代数角度证明一下这个式子,最后介绍两个它的应用
代数证明
根据文章开头反演原理部分的讨论,加上这个公式的对称性,我们只需要证明

这里 
好,现在我们来证明它,首先需要一个二项式系数的知识
如果运用组合推理就相当于是,你有一个  元素集
元素集  ,现在对
,现在对  进行计数,其中
进行计数,其中  且
且  ,首先对
,首先对  计数,
计数, 的
的  子集有
子集有  ,然后对
,然后对  计数,
计数, 的
的  子集有
子集有 
接下来换一种方式,先对  进行计数,
进行计数, 显然是
显然是  的子集,有
的子集,有  种方案,由于要求
种方案,由于要求  ,
, 中
中  个元素必须在
个元素必须在  中,
中, 还剩下
还剩下  个不确定的元素,
个不确定的元素, 还有
还有  个可以用的元素,一共有
个可以用的元素,一共有  种,于是就得到上面的恒等式,那么可以得到
种,于是就得到上面的恒等式,那么可以得到
这样最后就可以得到
于是,反演公式就建立了!
容斥原理证明
实际上,二项式反演是容斥原理(inclusion-exclusion principle)的一种最常见的特例子,让我们先来回忆一下容斥原理
设集合  中具有性质
中具有性质  的对象的集合为
的对象的集合为  ,那么不具有这些性质的对象的集合大小为
,那么不具有这些性质的对象的集合大小为
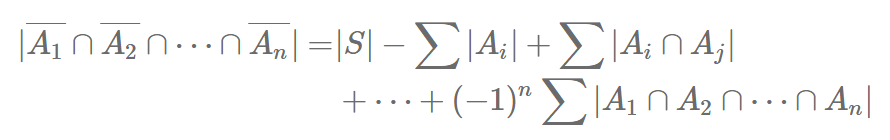
那么,考虑这样一种特殊的情况,若对于集族  中任意
中任意  个集合的并集的大小都是
个集合的并集的大小都是  ,我们不妨设
,我们不妨设

明显的,在  中一共有
中一共有  个这样的不同交集。另外,我们定义
个这样的不同交集。另外,我们定义 
这样一来,上面的容斥结果就是

由于  中任意
中任意  个集合的交集大小都是
个集合的交集大小都是  ,上面的公式左边的项也只和集合个数有关,我们可以设
,上面的公式左边的项也只和集合个数有关,我们可以设

同样令  ,那么同样使用容斥原理
,那么同样使用容斥原理
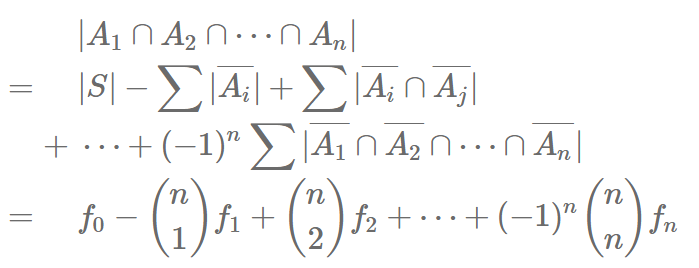
这也正是  的表达式,因此,整个证明就完成了!
的表达式,因此,整个证明就完成了!
应用
错位排列问题
求有多少个长度为  的排列
的排列  ,满足对于所有的
,满足对于所有的  ,使得
,使得 
这个问题有很多解法,我们来介绍一个有意思的解法:
为了叙述方便,我们称位置  是不变的当且仅当
是不变的当且仅当 
首先我们知道,如果不考虑  这个条件,问题是很简单的,长度为
这个条件,问题是很简单的,长度为  的排列一共有
的排列一共有  种。并且这些排列是由恰好有
种。并且这些排列是由恰好有  个位置是不变的排列组成,也就是,如果我们设
个位置是不变的排列组成,也就是,如果我们设  为恰好有
为恰好有  个位置是不变的排列的个数,那么可以得到
个位置是不变的排列的个数,那么可以得到

是否觉得和刚刚的反演公式很相似?这里的  就是
就是  ,那么,使用二项式反演可以得到
,那么,使用二项式反演可以得到

这也就是我们熟悉的错位排列
球染色问题
有  个球排成一行,你有
个球排成一行,你有  种颜色,要求给每一个球染色,相邻两个球颜色不可以相同,并且每种颜色至少使用一次
种颜色,要求给每一个球染色,相邻两个球颜色不可以相同,并且每种颜色至少使用一次
这是经常在高中数学组合那个部分见到的一个问题,只不过高中题目中数都很小
还是和刚刚的想法一样,如果没有每种颜色至少一次这个条件,那么问题很简单,答案是  。这些方案是由恰好使用了
。这些方案是由恰好使用了  种颜色的方案组成的,那么设
种颜色的方案组成的,那么设  为恰好使用了
为恰好使用了  种颜色的方案数,可以得到
种颜色的方案数,可以得到

经过反演得到








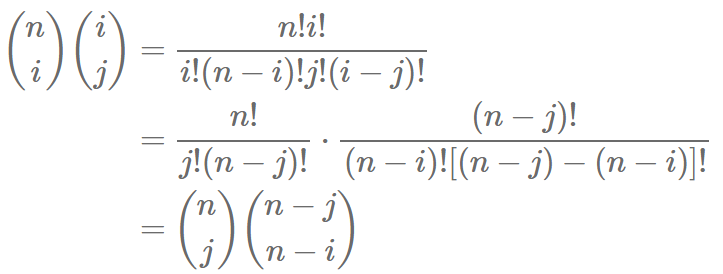
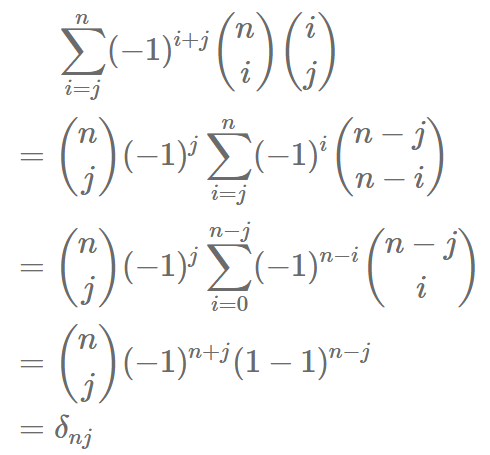














 922
922











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








