hihoCoder 1234 fractal

#1234 : Fractal

时间限制: 1000ms

单点时限: 1000ms

内存限制: 256MB

描述

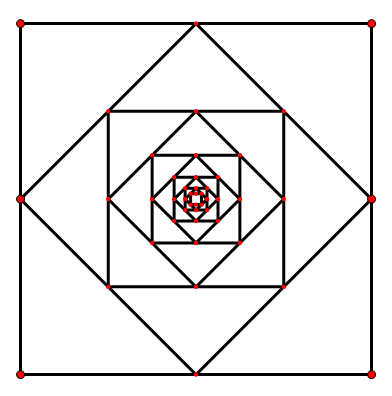
This is the logo of PKUACM 2016. More specifically, the logo is generated as follows:

1. Put four points A₀(0,0), B₀(0,1), C₀(1,1), D₀(1,0) on a cartesian coordinate system.

2. Link A₀B₀, B₀C₀, C₀D₀, D₀A₀ separately, forming square A₀B₀C₀D₀.

3. Assume we have already generated square A_iB_iC_iD_i, then square A_i+1B_i+1C_i+1D_i+1 is generated by linking the midpoints of A_iB_i, B_iC_i, C_iD_i and D_iA_i successively.

4. Repeat step three 1000 times.

Now the designer decides to add a vertical line x=k to this logo( 0<= k < 0.5, and for k, there will be at most 8 digits after the decimal point). He wants to know the number of common points between the new line and the original logo.

输入

In the first line there’s an integer T( T < 10,000), indicating the number of test cases.

Then T lines follow, each describing a test case. Each line contains an float number k, meaning that you should calculate the number of common points between line x = k and the logo.

输出

For each test case, print a line containing one integer indicating the answer. If there are infinity common points, print -1.

样例输入

3
0.375
0.001
0.478

样例输出

-1
4
20

 

重复1000次是个幌子，根本没有那么极端的数据，实际上重复到50多次就全是0.500000……了（用double)

所以不用纠结循环500还是循环1000，更不用纠结是501还是499.只要循环50就够了。

#include<math.h>
#include<stdio.h>
#include<string.h>
#include<string>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 1234

int n,flag,b[N];
double x,a[N];
const double eps = 1e-12;

void init()
{
    a[0] = 0.0;
    b[0] = 0;
    double f = 1.0 / 4;
    for(int i = 1; i <= 50; i++)
    {
        a[i] += a[i-1] + f;
        b[i] = b[i-1] + 4;
        f = f / 2;
    }
//    for(int i = 1; i <= 55; i++)
//    {
//        printf("%.60f\n ", a[i]);
//    }
}

int main()
{
    init();
    int T;cin>>T;
    while(T--)
    {
        scanf("%lf", &x);
        if(x > 0.5) x = 1 - x;
        for(int i = 0; i <= 50; i++)
        {
            if(fabs(x - a[i]) < eps)
            {
                printf("-1\n");
                break;
            }
            else if(x < a[i] && x > a[i-1])
            {
                printf("%d\n", b[i]);
                break;
            }
        }
    }

    return 0;
}

/*
3
0.375
0.001
0.478

*/

 

转载于:https://www.cnblogs.com/wmxl/p/4823265.html