[LOJ#2329]「清华集训 2017」我的生命已如风中残烛

最新推荐文章于 2024-04-29 15:53:56 发布

weixin_30326741

最新推荐文章于 2024-04-29 15:53:56 发布

阅读量116

点赞数

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/xiao-ju-ruo-xjr/p/8058382.html

版权

[LOJ#2329]「清华集训 2017」我的生命已如风中残烛

试题描述

九条可怜是一个贪玩的女孩子。

这天她在一堵墙钉了 \(n\) 个钉子，第 \(i\) 个钉子的坐标是 \((x_i,y_i)\)。接着她又在墙上钉上了 \(m\) 根绳子，绳子的一端是点 \(s_i(sx_i,sy_i)\)，绳子经过点 \(t_i(tx_i,ty_i)\)，同时绳子的长度是 \(L_i\)。其中 \(s_i\) 点是粘在墙上的，而另一个端点是可以移动的。初始情况下绳子是紧绷的一条直线段。

接着，对每一根绳子可怜都进行了一次游戏。在第 \(i\) 次游戏中，可怜会捏着第 \(i\) 根绳子的活动端点进行顺时针移动，移动过程中每时每刻绳子都是紧绷的。

不难发现绳子每时每刻都在以某一个位置为圆心作顺时针的圆周运动。初始情况下圆心是绳子的固定端点 \(s\)，但是在运动的过程中圆心可能会不断发生变化，如下图所示：

QAQ

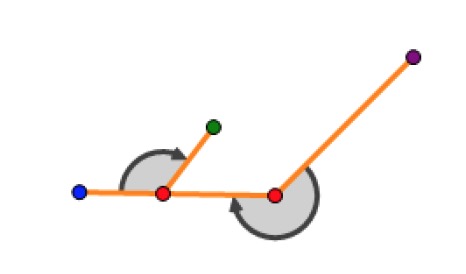
图中左侧红点为钉子所在的点，右侧红点为绳子的固定端点，其他颜色的点为虚拟点，活动端点为紫点；绳子从紫点开始运动，在运行到蓝点时绳子绕上左侧红点的钉子，因此活动端点更换了圆心和半径，继续作顺时针的圆周运动。接着活动端点会运行到绿点，并且接下来活动端点会一直绕左侧钉子不停地做圆周运动。

不难发现绳子的运动是不会停止的，因此可怜在她感觉累了之后就会停下来。但是作为一个好奇心满满的女孩子，可怜决定对每一根绳子计算一下如果绳子无限的运行下去，那么它的圆心会切换多少次（包括初始的圆心）。不难发现这个数值一定是有限的。

这里对游戏过程进行一定程度的假设来简化问题：

活动端点在运动的过程中距离每一个钉子的欧几里得距离始终大于等于 \(9 \times 10^{-4}\)。
钉子的坐标两两不同但可能有多点共线。

*钉子的体积以及绳子的体积可以忽略不计。在游戏的过程中每一段绳子之间不会互相影响。

初始情况下绳子距离每一个钉子的最近欧几里得距离大于等于 \(9 \times 10^{-4}\)。
每一根绳子初始粘着的端点不会影响绳子的运动，即绳子不会绕回到端点上。

输入

从标准输入读入数据。

第一行输入一个整数 \(T\)，表示数据组数。

每组数据第一行为两个整数 \(n,m\)，表示钉子数和绳子数。

接下来 \(n\) 行，每行两个整数 \(x_i,y_i\) 表示钉子的坐标。

接下来 \(m\) 行，每行五个整数 \(sx_i,sy_i,tx_i,ty_i,L_i\) 表示一段绳子，含义如上所述。

输出

输出到标准输出。

对于每组数据的每组询问，输出一行一个整数表示运行的过程中圆心变化了多少次。

不同数据组数之间无需空行隔开。

输入示例

2
5 3
0 0
2 0
2 2
0 2
1 1
1 3 10 3 10
1 3 10 3 20
1 3 10 3 30
3 1
0 0
100 0
1000 0
1 3 10 3 1000000000

输出示例

数据规模及约定

对于前 \(10\%\) 的数据，\(n \leq 2\)。

对于前 \(20\%\) 的数据，\(n \leq 3\)。

对于前 \(30\%\) 的数据，\(n \leq 10\)。

对于前 \(60\%\) 的数据，\(n \leq 100\)，\(m \leq 100\)。

对于 \(100\%\) 的数据，\(1 \leq n \leq 500\)，\(1 \leq m \leq 500\)，\(1\leq T \leq 10\)。

对于 \(100\%\) 的数据，\(0 \leq |x_i|,|y_i|,|sx_i|,|sy_i|,|tx_i|,|ty_i| \leq 10^4\)，\(1 \leq L_i \leq 10^9\)。

题解

妈妈呀我终于卡过这题了！

等等我需要冷静一下才能写题解……

思路很直接，我们先考虑暴力，每次以一个点为原点，将所有点按照极角排序（\(O(n \mathrm{log}n)\)），然后再根据当前极角和剩余长度暴力扫一遍找到下一个点（\(O(n)\)）。然后有可能出现循环，这个东西可以判一下如果一个点经过了两次并且这两次到达这个点时极角都一样，就表明找到了一个循环；那么可以算一下这个循环会被跑多少圈，跑完后增加多少步、剩下多少长度。这样做总共会有 \(n \mathrm{log}L\) 次转折点（考虑每经过一个循环就会使长度对某个数取模，即 \(L\) 最坏也会变成 \(\frac{L}{2}\)，当 \(L\) 小于 \(1\) 时，由于是整点，就不可能再碰到其他点了），\(m\) 组询问，所以总复杂度 \(O(Tmn^2 \mathrm{log}L \mathrm{log}n)\)（对了还要乘个 \(T\)），纵然有 \(10\) 秒，也过不去啊……（~~像我这种 \(O(n^3)\) 都卡了一年才卡线过的……~~）

瓶颈在于每次“找下一个点”的操作太费时了。考虑用预处理的方式优化。我们令 \(A(x, y, z)\) 表示轴心在点 \(x\)，方向指向点 \(y\)，当长度为 \(z\) 的时候恰好可以走到的下一个节点编号。那么预处理的时候我们先枚举点 \(x\)，然后以 \(x\) 为原点极角排序，接下来一遍 \(O(n^2)\) 就可以搞定了。那么在询问时只需要二分一下极角，然后再二分一下长度，就可以在 \(O(\mathrm{log}n)\) 的时间内找到下一个点了。

最后贴上我又臭又长的代码。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <vector>
#include <cmath>
#include <ctime>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)

const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
    if(Head == Tail) {
        int l = fread(buffer, 1, BufferSize, stdin);
        Tail = (Head = buffer) + l;
    }
    return *Head++;
}
int read() {
    int x = 0, f = 1; char c = getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}

#define maxn 501
#define LD long double

const LD eps = 1e-9;

struct Vec {
    int x, y;
    Vec() {}
    Vec(int _, int __): x(_), y(__) {}
    
    LD operator - (const Vec& t) const {
        return sqrt((LD)(x - t.x) * (x - t.x) + (LD)(y - t.y) * (y - t.y));
    }
} ps[maxn], BaseP;

int n, id[maxn], nsiz[maxn][maxn], nxt[maxn][maxn][maxn], angsiz[maxn];
double angle[maxn][maxn], pairAng[maxn][maxn], pairDis[maxn][maxn];

int Base;
inline bool cmp(const int& A, const int& B) {
    Vec a = ps[A], b = ps[B];
    LD anga = pairAng[Base][A], angb = pairAng[Base][B],
           disa = a - ps[Base], disb = b - ps[Base];
    return fabs(anga - angb) > eps ? anga < angb : disa > disb;
}
inline bool cmp2(const int& A, const int& B) {
    Vec a = ps[A], b = ps[B];
    LD anga = atan2(a.x - BaseP.x, a.y - BaseP.y), angb = atan2(b.x - BaseP.x, b.y - BaseP.y),
           disa = a - BaseP, disb = b - BaseP;
    return fabs(anga - angb) > eps ? anga < angb : disa > disb;
}

void init() {
    rep(i, 1, n) id[i] = i;
    rep(S, 1, n) rep(T, 1, n) {
        nsiz[S][T] = 0;
        if(S != T) pairAng[S][T] = atan2(ps[T].x - ps[S].x, ps[T].y - ps[S].y), pairDis[S][T] = ps[S] - ps[T];
    }
    rep(S, 1, n) {
        Base = S;
        sort(id + 1, id + n + 1, cmp);
        int cnt = 0;
        rep(T, 1, n) if(S != id[T] && (T == 1 || fabs(pairAng[S][id[T]] - pairAng[S][id[T-1]]) > eps)) {
            angle[S][++cnt] = pairAng[S][id[T]];
            rep(I, T + 1, n) if(id[I] != S && fabs(angle[S][cnt] - pairAng[S][id[I]]) > eps)
                if(!nsiz[S][cnt] || pairDis[S][nxt[S][cnt][nsiz[S][cnt]-1]] > pairDis[S][id[I]]) nxt[S][cnt][nsiz[S][cnt]++] = id[I];//*/
            rep(I, 1, n) if(id[I] != S) {
                if(!nsiz[S][cnt] || pairDis[S][nxt[S][cnt][nsiz[S][cnt]-1]] > pairDis[S][id[I]]) nxt[S][cnt][nsiz[S][cnt]++] = id[I];
                if(angle[S][cnt] < pairAng[S][id[I]]) break;
            }
        }
        angsiz[S] = cnt;
    }
    return ;
}

LD atLen[maxn];
int atTag[maxn], hasPass[maxn];
int getAns(int p, LD ang, LD L) {
    memset(atTag, 0, sizeof(atTag));
    memset(hasPass, 0, sizeof(hasPass));
    memset(atLen, 0, sizeof(atLen));
    int tot = 1;
    while(1) {
        if(ang < angle[p][1]) ang = 1.0 / 0.0;
        int dir;
        int l = 1, r = angsiz[p] + 1;
        while(r - l > 1) {
            int mid = l + r >> 1;
            if(angle[p][mid] <= ang) l = mid; else r = mid;
        }
        dir = l;
        
        l = 0; r = nsiz[p][dir] - 1;
        while(l < r) {
            int mid = l + r >> 1;
            if(mid < nsiz[p][dir] - 1 && pairDis[nxt[p][dir][mid]][p] > L) l = mid + 1; else r = mid;
        }
        if(pairDis[nxt[p][dir][l]][p] > L) break;
        
        ang = pairAng[p][nxt[p][dir][l]];
        L -= pairDis[nxt[p][dir][l]][p]; tot++;
        p = nxt[p][dir][l];
        if(atTag[p]) {
            int cyc = (int)(L / (atLen[p] - L));
            tot += (tot - atTag[p]) * cyc;
            L -= (atLen[p] - L) * cyc;
        }
        if(hasPass[p]) atTag[p] = tot, atLen[p] = L;
        else hasPass[p] = 1;
    }
    return tot;
}

void work() {
    n = read(); int q = read();
    rep(i, 1, n) {
        int x = read(), y = read();
        ps[i] = Vec(x, y);
    }
    init();
    while(q--) {
        int sx = read(), sy = read(), tx = read(), ty = read(), L = read();
        Vec s(sx, sy), t(tx, ty);
        LD ang = atan2(t.x - s.x, t.y - s.y);
        BaseP = Vec(sx, sy);
        sort(id + 1, id + n + 1, cmp2);
        bool has = 0;
        rep(I, 1, n) {
            Vec i = ps[id[I]];
            LD nang = atan2(i.x - s.x, i.y - s.y);
            if(nang >= ang && L > i - s){ printf("%d\n", getAns(id[I], nang, L - (i - s)) + 1); has = 1; break; }
        }
        if(!has) {
            ang = -1.0 / 0.0;
            rep(I, 1, n) {
                Vec i = ps[id[I]];
                LD nang = atan2(i.x - s.x, i.y - s.y);
                if(nang >= ang && L > i - s){ printf("%d\n", getAns(id[I], nang, L - (i - s)) + 1); has = 1; break; }
            }
        }
        if(!has) puts("1");
    }
    return ;
}

int main() {
    int T = read();
    while(T--) work();
    
    return 0;
}

~~调得我已然成了风中残烛~~

转载于:https://www.cnblogs.com/xiao-ju-ruo-xjr/p/8058382.html

weixin_30326741

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
[LOJ#2329]「清华集训 2017」我的生命已如风中残烛

[LOJ#2329]「清华集训 2017」我的生命已如风中残烛试题描述九条可怜是一个贪玩的女孩子。这天她在一堵墙钉了 \(n\) 个钉子，第 \(i\) 个钉子的坐标是 \((x_i,y_i)\)。接着她又在墙上钉上了 \(m\) 根绳子，绳子的一端是点 \(s_i(sx_i,sy_i)\)，绳子经过点 \(t_i(tx_i,ty_i)\)，同时绳子的长度是 \(L_i\)。其中 \(s_i...
复制链接

扫一扫