前言
最大流问题是网络优化中典型的问题,用形象的语言来描述就是在满足容量约束的前提下将尽可能多的流从源节点(始点)到汇节点(终点)。解决此问题的经典方法很多,本文介绍广为人熟知的Ford-Fulkerson算法,来解决最大流问题。尽管网上关于此问题的文章多如牛毛,但笔者希望结合自己学习过程中对算法的理解,给予算法最清晰的介绍,希望对大家有帮助。(笔者曾尝试使用java来实现,但最终因用java实现和使用图太麻烦了,又不想重新用python来实现,故放弃,以后的实现估计会采用python而不是java,java毕竟不适合写图相关算法)。
一、知识准备
学习此算法前建议读者学习网络流相关知识和基本概念,一些需要了解的概念和知识先罗列如下
1、可增广路
2、最大流最小割定理
3、图的割集
4、饱和割集
5、可行流向量
6、节点的散度
7、前向后向边
二、可增广路搜索算法
对于k=0,1,..., 给定Tk, 若Tk为空集或者t∈Tk则算法终止。否则,令
Tk+1 = { Tk | 存在节点m∈Tk, 以及边(m, n) 满足xmn < cmn, 或者边(n, m) 满足 bnm<xnm},
(其中节点数为n,bnm和cnm为边mn容量的最小和最大值,xmn为边的流量, Tk+1集合的节点不能属于T其他集合节点)
上式的含义即为Tk+1为在集合Tk中所有节点满足可增广路条件的相邻的节点组成的集合,当然,这些节点不能包括已经存在其他T集合中的节点。
当算法终止时,最后一个集合Tk有两种情况(假设s为起点, t为终点):
(1) 最后一个集合Tk包含t,此时从t向前标记即可构造从s到t的简单可增广路。即从T1,T2,T3,....,Tk中每个取一个节点的路
(2)最后一个集合Tk为空集,此时得到一个分离s和t的饱和割集
现举例说明,如下图(容量下限(最小值),流量,容量上限(最大值))标在每条边旁
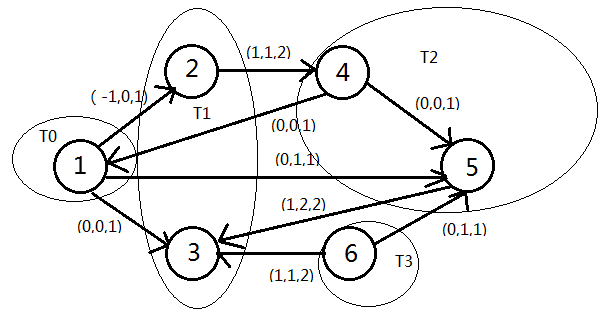
1为源点,6为汇点。开始T0只有1个节点,就是节点1。接下来从和T0中节点,也就是节点1相邻的节点2和3开始。边12,流量为0,为前向边,满足流量小于容量上限;边13也为前向边,满足流量小于上限(0 < 1)。所以节点2和节点3组成T1。然后考虑以节点2和节点3来寻找T2,原理和前面一致,其中边35,为后向边,流量为2,大于容量下限1,所以节点5添加到T2,。到最后T3,集合包含6,终止。此时增广路为(1,3,5,6)。
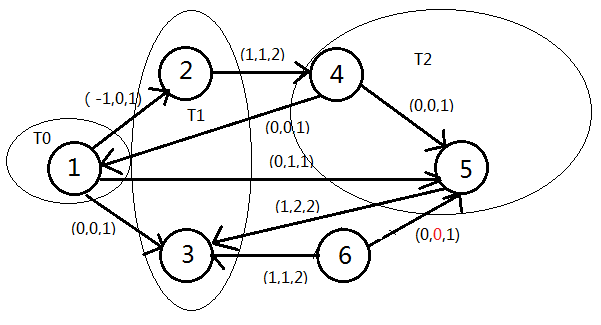
现在看另一图,只是把边56的流量改为了0,此时后向边56不满足流量大于下限,所以T3为空集。此时存在饱和割集{S, N-S}分离1和6,其中S = {1,2,3,4,5},是所有集合Tk的并集
三、Ford-Fulkerson算法
在了解了可增广路搜索算法后,现在正式进入本文的主题,Ford-Fulkerson算法。该算法在每次迭代中改进原费用(s的散度),因此是原费用改进型算法。算法思想是,给定可行流向量x(即满足容量可行且除了s和t之外节点的散度为零,即节点流入和流出相等,的流向量),以及对于x可增广的从s到t的路P,就可以增进P的前向边(i,j)的流量并减小P的后向边(i,j)的流量。流量增量的最大值为
δ = min{ {cij - xij | (i, j) ∈ P+}, {xij - bij | (i, j) ∈ P-} }, 其中P+是P的前向边的集合, P-是P的后向边的集合。
由此得到的流向量y由
yij = :xij + δ 如果(i, j) ∈ P+,
xij - δ 如果(i,j) ∈P-,
算法的迭代步骤
使用可增广路搜索算法实现下述两种情况之一:
(1)、得到将s和t分离的饱和割集
(2)、得到从s到t的x的可增广路P。
在情况1下,算法终止;此时的流向量即为所求。在情况2下,沿着P进行增广,并进行下一次迭代。每次增广时,算法通过增广增量δ改进原费用(s的散度)。现在以例子说明
初始图,如图1。搜索到增广路(1, 2, 5),路12和路25为正向边,求δ=min{ c12- x12, c25- x25}为1。如图2
 图1
图1
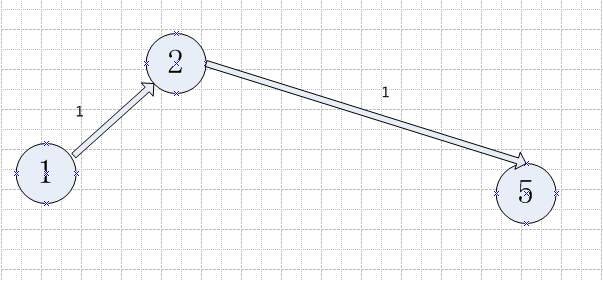 图2
图2
对增广路中的所有边x12和x25使用δ改进费用,因为均为正向边,有新的流量为x12=0 + 1 = 1, x25= 0 + 1 = 1。费用改进后如图3。费用改进后继续寻找增广路,如图4。
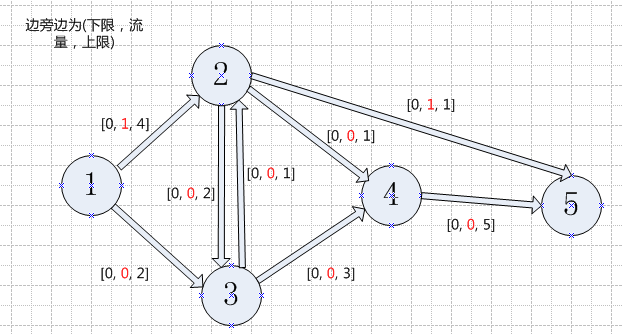 图3
图3
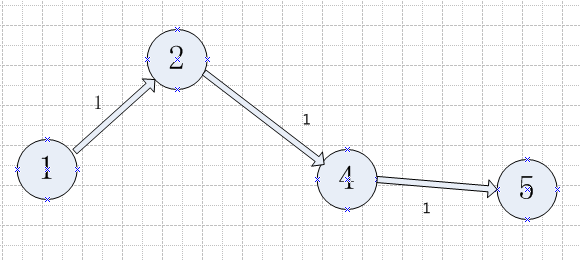 图4
图4
迭代
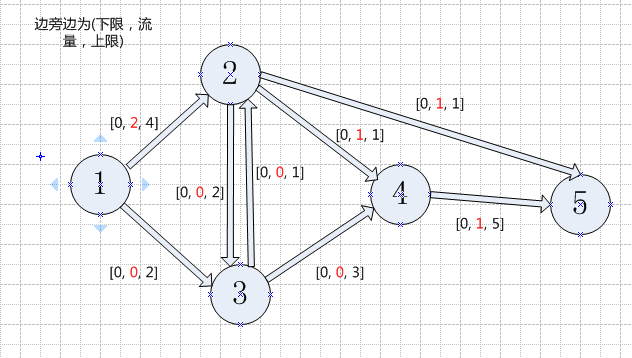 图5
图5
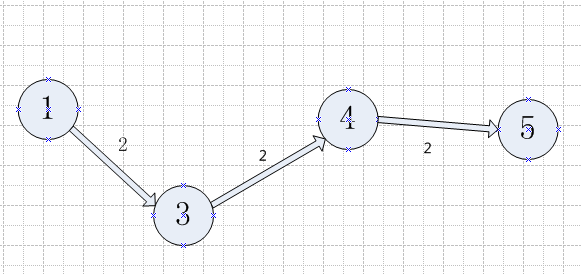 图6
图6
迭代
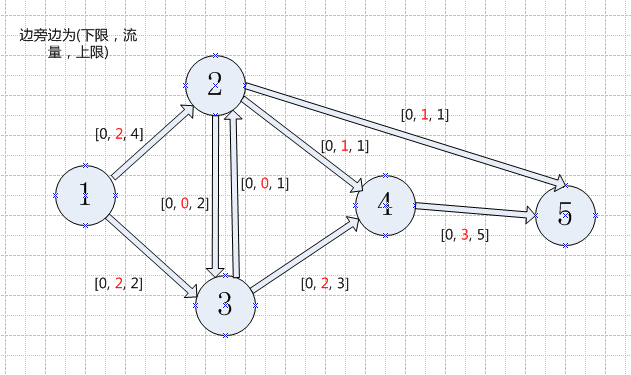 图7
图7
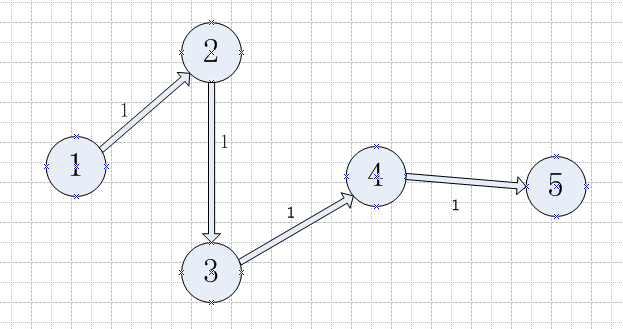 图8
图8
在最后一次费用改进后,已找不到增广路。其中T0包含节点1,T1包含节点2,T3包含节点3,因此饱和割集为[{1, 2, 3}, {4, 5}]。割集容量即为最大容量,即5=c24 + c34 + c25 = 5
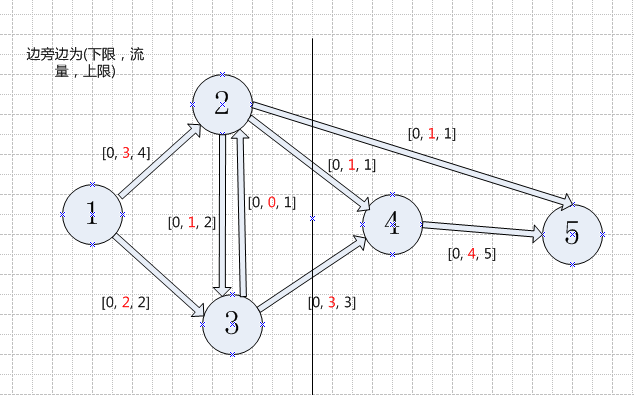 图9
图9
四、
在学习此算法时,笔者已经尽力描述算法的主要内容了。由于需要有一些图论的知识作为辅助,加上算法有些复杂,所以结合文中例子效果会更好。
五、知识相关




















 5445
5445











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








