一、 填空题
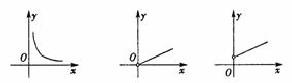
1. 一般地,函数 是反比例函数,其图象是__________,当![]() >0时,图象两支在__________象限内,在每个象限内y随x的增大而 。当
>0时,图象两支在__________象限内,在每个象限内y随x的增大而 。当![]() 时,图象两支在__________象限内,在每个象限内y随x的增大而
时,图象两支在__________象限内,在每个象限内y随x的增大而
3. 写出一个反比例函数,使得这个反比例函数的图像在第一、三象限,这个函数是 ;且写出这个函数上一个点的坐标是 ;
4. 若函数y=4x与y=![]() 的图象有一个交点是(
的图象有一个交点是(![]() ,2),则另一个交点坐标是 。
,2),则另一个交点坐标是 。
5.设有反比例函数![]() ,
,![]() ,
,![]() 为其图象上两个点,若x1<0<x2,y1>y2,则k的取值范围_________。
为其图象上两个点,若x1<0<x2,y1>y2,则k的取值范围_________。
6.直线y=kx+b过一、三、四象限,则函数![]() 的图象在____________象限,并且在每一个象限内,y随x的增大而______________ 。
的图象在____________象限,并且在每一个象限内,y随x的增大而______________ 。
7.反比例函数![]() 的图象经过(-
的图象经过(-![]() ,5)点、(a,-3)及(10,b)点,则k= ,a= ,b= ;
,5)点、(a,-3)及(10,b)点,则k= ,a= ,b= ;
8.已知y-2与x成反比例,当x=3时,y=1,则y与x间的函数关系式为 ;
9.己知反比例函数![]() (x >0),y随x 的增大而增大,则m的取值范围是 ;
(x >0),y随x 的增大而增大,则m的取值范围是 ;
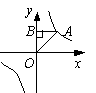
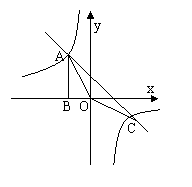
10.如图,点A是反比例函数![]() 图象上一点,AB⊥y轴于点B,那么△AOB的面积是 ;
图象上一点,AB⊥y轴于点B,那么△AOB的面积是 ;
二. 选择题
11. 下列函数中,是反比例函数的是( )
13.如果反比例函数![]() 的图像经过点(-3,-4),那么函数的图像应在( )
的图像经过点(-3,-4),那么函数的图像应在( )
A、 第一、三象限 B、 第一、二象限 C、 第二、四象限 D、 第三、四象限
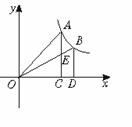
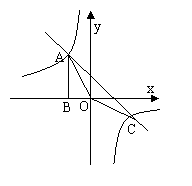
5. 如图,过反比例函数y=![]() (x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得( )
(x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得( )
A.S1>S2 B.S1<S2 C.S1=S2 D.S1、S2的大小关系不能确定
16.在第三象限中,下列函数,y随x的增大而减小的有( )。
①、y= -![]() ②、y =
②、y =![]() ③、y = - 2x+5 ④、y = - 5x-6
③、y = - 2x+5 ④、y = - 5x-6
A、1个 B、2个 C、3个 D、4个
A. 0 B. 1 C. 2 D. 不确定
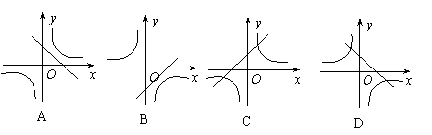
18. 如果变阻器两端电压不变,那么通过变阻器的电流y与电阻x的函数关系图象大致是( )
A B C D
19. 若y与x成正比,y与z的倒数成反比,则z是x的( )
A. 正比例函数 B. 反比例函数 C. 二次函数 D. z随x增大而增大
三. 解答题
(1)求这个函数的解析式;
21. 如图,A为双曲线上一点,过A作AC⊥x轴,垂足为C,且S△AOC=2.
(1) 求该反比例函数解析式;
(2) 若点(-1,y1),(-3,y2)在双曲线上,试比较y1、 y2的大小.
22. 已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象的一个交点为P(a,b),且P到原点的距离是10,求a、b的值及反比例函数的解析式。
的图象的一个交点为P(a,b),且P到原点的距离是10,求a、b的值及反比例函数的解析式。
23. 已知三角形的面积为30cm2,一边长为acm,这边上的高为hcm.
(1)写出a与h的函数关系式.(2)在坐标系中画出此函数的简图.
(3)若h=10cm,求a的长度?
24.某空调厂的装配车间原计划用2个月时间(每月以30天计算),每天组装150台空调.
(1)从组装空调开始,每天组装的台数m(单位: 台/天)与生产的时间t(单位:天)之间有怎样的函数关系?
(2)由于气温提前升高、厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少空调?
25. 制作一种产品,需先将材料加热达到![]() ℃后,再进行操作.设该材料温度为
℃后,再进行操作.设该材料温度为![]() (℃),从加热开始计算的时间为
(℃),从加热开始计算的时间为![]() (分钟).据了解,设该材料加热时,温度
(分钟).据了解,设该材料加热时,温度![]() 与时间
与时间![]() 成一次函数关系;停止加热进行操作时,温度
成一次函数关系;停止加热进行操作时,温度![]() 与时间
与时间![]() 成反比例关系(如图).已知该材料在操作加工前的温度为
成反比例关系(如图).已知该材料在操作加工前的温度为![]() ℃,加热5分钟后温度达到
℃,加热5分钟后温度达到![]() ℃.
℃.
(1)分别求出将材料加热和停止加热进行操作时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)根据工艺要求,当材料的温度低于![]() ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
26.如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是![]() ,
,
求:(1)一次函数的解析式;
(2)△AOB的面积.
(1)若一次函数和反比例函数的图象相交于点(-3,m),求m和k的值.
(2)当k=-2时,设这两个函数图象的交点分别为A、B,试判断此时A、B两点分别在第几象限?∠AOB是锐角还是钝角?(只要求直接写出结论)
28如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥![]() 轴于B且S△ABO=
轴于B且S△ABO=![]() .
.
(1)求这两个函数的解析式.
(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积.
(3)在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的点P的坐标求出来,若不存在,请说明理由.
已知反比例函数y=![]() (k﹤0)的图象上有两点A(
(k﹤0)的图象上有两点A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),且
),且![]() ﹤
﹤![]() ,则
,则![]() -
-![]() 的值是( )
的值是( )
(A)正数 (B)负数 (C)非正数 (D)不能确定
如图所示是三个反比例函数y=![]() ,y=
,y=![]() ,y=
,y=![]() 的图象,由此观察
的图象,由此观察![]() 、
、![]() 、
、![]() 的大小关系是 (用“﹤”连接)
的大小关系是 (用“﹤”连接)
某空调厂的装备车间计划组装9000台空调:
(1)从组装空调开始,每天组装的台数m(单位:台/天)与生产的时间t(单位:天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少空调?
如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=![]() (k﹥0,x﹥0)的图象上,点P(m,n)是函数 y=
(k﹥0,x﹥0)的图象上,点P(m,n)是函数 y=![]() (k﹥0,x﹥0)的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(k﹥0,x﹥0)的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(1)求B点坐标和k的值。
(3)写出S关于m的函数关系式。
如图,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 在第一象限交于B、C两点,且AB·AC=4,则k=_________.
在第一象限交于B、C两点,且AB·AC=4,则k=_________.
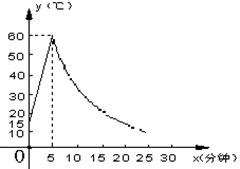
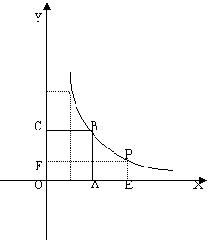
为了预防流感,某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
⑴ 写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
⑵ 据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
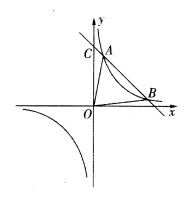
如图正比例函数y=k1x与反比例函数![]() 交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4。
交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4。
①分别求出正比例函数与反比例函数的解析式。
②求出正、反比例函数图像的另外一个交点坐标。
③求△ODC的面积。
如图,正比例函数y=½x与反比例函数![]() 的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
(1)求k的值;(2)求A、B两点的坐标;
(3)在![]() 轴的正半轴上是否存在一点P,使得△POA为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
轴的正半轴上是否存在一点P,使得△POA为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.

如图已知一次函数![]() 与x轴、y轴分别交于点D、C两点和反比例函数
与x轴、y轴分别交于点D、C两点和反比例函数![]() 交于A、B两点,且点A的
交于A、B两点,且点A的
坐标是(1,3)点B的坐标是(3,m)求a,k,m的值;
(1) 求C、D两点的坐标,并求△AOB的面积;
如图,点P是直线![]() 与双曲线
与双曲线![]() 在第一象限内的一个交点,直线
在第一象限内的一个交点,直线![]() 与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9.
与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9.
(1)求k的值;(2)求△PBC的面积.
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当![]() 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?
(3)![]() 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中![]() 过点
过点![]() 作直线
作直线![]() 轴,交y轴于点
轴,交y轴于点![]() ;过点
;过点![]() 作直线
作直线![]() 轴交
轴交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当四边形
.当四边形![]() 的面积为6时,请判断线段
的面积为6时,请判断线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
(1)探究新知:
如图1,已知△ABC与△ABD的面积相等,则AB与CD的位置关系平行.
(2)结论应用:
① 如图2,点M,N在反比例函数y=k/x(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行.
如图,已知正比例函数和反比例函数的图像都经过点M(-2,-1),且P(-1,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;
如图所示,在直角坐标系中,点![]() 是反比例函数
是反比例函数![]() 的图象上一点,
的图象上一点,![]() 轴的正半轴于
轴的正半轴于![]() 点,
点,![]() 是
是![]() 的中点;一次函数
的中点;一次函数![]() 的图象经过
的图象经过![]() 、
、![]() 两点,并将
两点,并将![]() 轴于点
轴于点![]() 若
若![]()
(1)求反比例函数和一次函数的解析式;
如图所示,点P在经过B(0,-2),C(4,0)的直线上,且纵坐标为-1,Q点在y=![]() 的图象上,若PQ∥y轴,求Q点的坐标。
的图象上,若PQ∥y轴,求Q点的坐标。
某项工程需要砂石料2×106立方米,阳光公司承担了该工程运送砂石料的任务。
(1)在这项任务中平均每天的工作量v(立方米/天)与完成任务所需的时间t(天)之间具有怎样的函数关系?写出这个函数关系式。
(2)阳关公司计划投入A型卡车200辆,每天一共可以运送砂石料2×104立方米,则完成全部运送任务需多少天?如果工作了25天后,由于工程进度的需要,公司准备再投入A型卡车120辆,在保持每辆车每天工作量不变的前提下,问是否能提前28天完成任务?
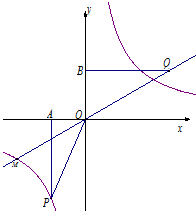
两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥x轴于点C,交
的图象上,PC⊥x轴于点C,交![]() 的图象于点A,PD⊥y轴于点D,交
的图象于点A,PD⊥y轴于点D,交![]() 的图象于点B,当点P在
的图象于点B,当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;
③PA与PB始终相等;
④当点A是PC的中点时,点B一定是PD的中点.
其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分).

如图,已知A(x1,y1),B(x2,y2)是双曲线y=![]() 在第一象限内的分支上的两点,连结OA、OB.
在第一象限内的分支上的两点,连结OA、OB.
(2)过B作BC⊥x轴于C,当m=4时,求△BOC的面积.
为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如图所示.据图中提供的信息,解答下列问题:
为常数),如图所示.据图中提供的信息,解答下列问题:
(1) 写出从药物释放开始,![]() 与
与![]() 之间的两个函数关系式及相应的自变量的取值范围;
之间的两个函数关系式及相应的自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到![]() 毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?







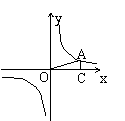

![clip_image004[7]](https://i-blog.csdnimg.cn/blog_migrate/88b4552b6080090101452984a45a4234.gif)

























 836
836

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








