最小支撑树树
前几节中介绍的算法都是针对无权图的,本节将介绍带权图的最小支撑树(minimum spanning tree)算法。给定一个无向图G,并且它的每条边均权值,则MST是一个包括G的所有顶点及边的子集的图,这个子集保证图是连通的,并且子集中所有边的权值之和为所有子集中最小的。
本节中介绍三种算法求解图的最小生成树:Prim算法、Kruskal算法和Boruvka算法。其中Prim算法将介绍两种实现方法,一种是普通的贪心算法;而第二种算法是借助最大堆的贪心算法,其性能更高。Prim算法的思路是从任意一个顶点开始,逐步向已形成的MST子树中增加权值最小的边从而最终形成MST。Kruskal算法和Boruvka算法类似,都是向MST子树的一个分布森林中增加边来构建MST。
这三种算法都是贪心算法,有关贪心算法的讨论请参阅相关书籍。贪心算法的思想是选择当时最佳的路径。一般而言,贪心策略不一定能保证找到全局最优解,但是对最小支撑树问题来说,贪心策略能获得具有最小权值的生成树。
本节将使用前面章节中介绍的广义树来返回图的最小生成树。实现上述三个算法的类名称为MinimumSpanningTree。
1 Prim算法
Prim算法可以说是所有MST算法中最简单的,比较适用于稠密图。以图中任意一个顶点S开始,选择与之相关连的边中权值最小的边加入到MST中,假设这条边的终点为T,则MST初始化为(S, T),称之为“当前MST”。接下来在剩余的边中选择与当前MST中s所有顶点相关连的边中权值最小的边,并添加到当前MST中。这一过程一直迭代到图中所有顶点都添加到MST中为止。
在迭代时,假设当前MST中顶点形成集合Vs,则对Vs中的每一个vi,遍历与其相邻的所有边,并找到权值最小的边。这一过程实现如下:
* @param 输入s:最小生成树的树根
* @return 函数返回时V,D,mst都重新赋值
*/
public void Prim( int s){
if(s < 0)
return;
int nv = G.get_nv();
// 初始化
for( int i = 0; i < nv; i++){
D[i] = Integer.MAX_VALUE;
V[i] = -2;
// 0 -- 没添加到树中
G.setMark(i, 0);
}
// 对起点s,父节点为-1,距离为0
V[s] = -1;
D[s] = 0;
G.setMark(s, 1);
// 将起点添加到广义树中
mst.addChild(0, s, new ElemItem<Double>(D[s]));
/* 在其余顶点中找到与当前MST最近的顶点v,并将顶点的父节点和
* 顶点v添加到MST中。其中图的权值存放在节点v中。
* 循环迭代,直至所有顶点都遍历一遍 */
while( true){
/* 获取与当前树距离最近的边,其终点为最近的顶点
* 终点为最近顶点的父节点 */
Edge E = Utilities.minNextEdge(G, V);
// 如果边为空,函数返回
if(E == null) return;
System.out.println(E.get_v1() + " -- "
+ E.get_v2() + " -- "
+ G.getEdgeWt(E));
// E的起点赋值给V[E的终点]
V[E.get_v2()] = E.get_v1();
// E的权值赋值给D[E的终点]
D[E.get_v2()] = G.getEdgeWt(E);
// E的终点被访问过了
G.setMark(E.get_v2(), 1);
// 在最小生成树中添加边E对应的信息
mst.addChild(E.get_v1(), E.get_v2(),
new ElemItem<Double>(D[E.get_v2()]));
}
}
函数中对MinimumSpanningTree的数组V和D的值进行更新,V[i]的值表示最小支撑树中中顶点i的父顶点,D[i]表示顶点i与其父顶点V[i]之间边的权值。函数最终向当前对象的mst(最小支撑树)中添加顶点,最终形成以起始顶点S为根节点的广义树树结果(左子节点右兄弟节点树)。
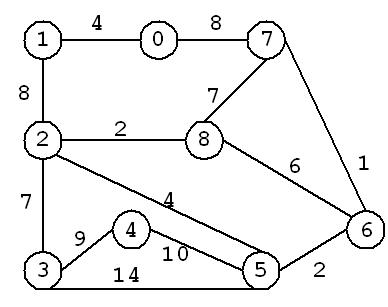
如图所示,以顶点0为起点求解图中最小支撑树。按照程序流程,构造MST的详细过程如图(1~8)所示。
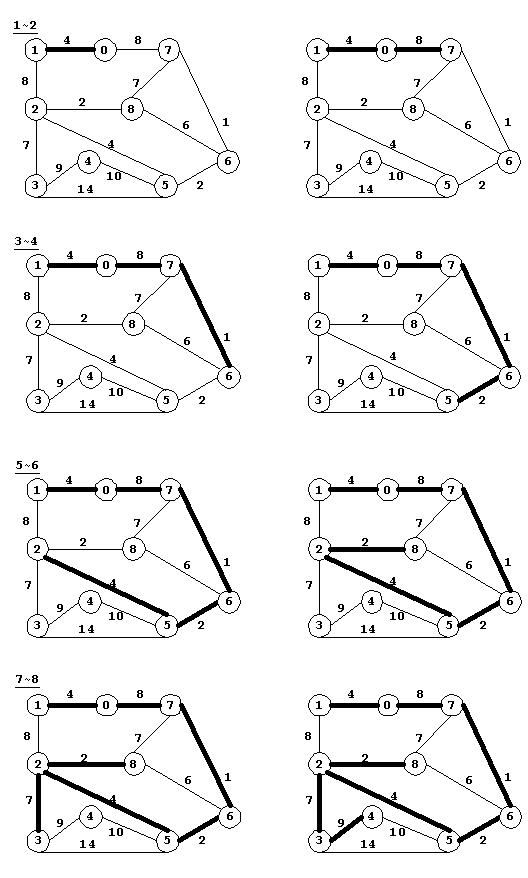
以图做为测试并检验函数。起始顶点0,测试程序如下:
GraphLnk GL =
Utilities.BulidGraphLnkFromFile("Graph\\graph7.txt");
MinimumSpanningTree MSTex = new MinimumSpanningTree(GL);
MSTex.Prim(0);
MSTex.mst.ford_print_tree();
System.out.println("各顶点的父节点:");
for( int i = 0; i < MSTex.V.length; i++){
System.out.print(MSTex.V[i] + ", ");
}
System.out.println("\n各顶点距其父节点距离:");
for( int i = 0; i < MSTex.D.length; i++){
System.out.print(( int)(MSTex.D[i]) + ", ");
}
}
0 -- 1 -- 4
0 -- 7 -- 8
7 -- 6 -- 1
6 -- 5 -- 2
5 -- 2 -- 4
2 -- 8 -- 2
2 -- 3 -- 7
3 -- 4 -- 9
9 节点,前序遍历打印:
|—— 0.0(0)
|—— 4.0(1)
|—— 8.0(7)
|—— 1.0(6)
|—— 2.0(5)
|—— 4.0(2)
|—— 2.0(8)
|—— 7.0(3)
|—— 9.0(4)
各顶点的父节点:
-1, 0, 5, 2, 3, 6, 7, 0, 2,
各顶点距其父节点距离:
0, 4, 4, 7, 9, 2, 1, 8, 2,
结果第一部分为各顶点添加到最小生成树mst中的顺序;第二部分为mst的前序遍历打印结果;最后一部分为各顶点在mst中的父节点以及与父节点形成的边在图中的权值。
2 基于优先队列的Prim算法
Prim算法的流程比较容易理解,算法可以在线性时间内找出图的MST。但是从实现过程可以发现,在遍历与顶点相邻的所有边寻找与当前MST最近的顶点时,需要进行循环判断,选择距离最近的边之后其余边的信息将被舍弃;在下次循环判断时这些舍弃的边又被再次参与“竞选”最近的边,这无疑带来了重复判断。
可以引入一个最小堆,堆中存放遍历过的边。在遍历与顶点相邻的所有边时,首先将连边添加到堆中,然后直接将堆顶的边取出并添加到MST中。这样就可以避免重复判断。算法的实现如下:
* 基于有线队列的Prim算法;
* 需要利用最小堆结构,但是我们之前只设计了最大堆,
* 所以将堆节点中用于表示大小关系的元素值乘以-1,
* 作用等效于最小堆;堆节点元素为 EdgeElem。
* @param 起始顶点s
*/
public void PrimPQ( int s){
if(s < 0) return;
// 图顶点和图边个数
int nv = G.get_nv();
int ne = G.get_ne();
// 堆最大为边的条数
MaxHeap H = new MaxHeap(ne);
// 初始化
for( int i = 0; i < nv; i++){
D[i] = Integer.MAX_VALUE;
V[i] = -2;
// 0 -- 没添加到树中
G.setMark(i, 0);
}
// 对起点s,父节点为-1,距离为0
V[s] = -1;
D[s] = 0;
G.setMark(s, 1);
// 将起点添加到广义树中
mst.addChild(0, s, new ElemItem<Double>(D[s]));
// 初始化堆,将与起点相连的边都添加到堆中
for(Edge E = G.firstEdge(s); G.isEdge(E); E = G.nextEdge(E)){
D[E.get_v2()] = G.getEdgeWt(E);
V[E.get_v2()] = s;
H.insert( new ElemItem<EdgeElem>
( new EdgeElem(E, -1 * G.getEdgeWt(E))));
}
H.printHeap();
// 将堆顶元素删去并返回
int v = -1;
EdgeElem PE = null;
while( true){
v = -1;
// 如果堆不为空
while(H.topVal() != null){
// 删除并返回堆顶元素
PE = (EdgeElem)(H.removeMax().elem);
H.printHeap();
v = PE.get_v2();
// 如果堆顶元素对应的顶点没有被访问,则退出循环
if(G.getMark(v) == 0)
break;
// 否则表示没有找到下一个可添加到MST的顶点
else v = -1;
}
// 如果没有可继续添加的顶点了,函数返回
if(v == -1)
return;
// 将得到的堆顶元素对应顶点重置为访问过
G.setMark(v, 1);
// 在最小生成树中添加边E对应的信息
mst.addChild(PE.get_v1(), PE.get_v2(),
new ElemItem<Double>(D[PE.get_v2()]));
// 继续将与v相连的、未经访问的边添加到堆中
for(Edge w = G.firstEdge(v); G.isEdge(w); w = G.nextEdge(w)){
// 顶点尚未被访问过,并且不在堆中
if(G.getMark(w.get_v2()) == 0
&& D[G.edge_v2(w)] > G.getEdgeWt(w)){
D[G.edge_v2(w)] = G.getEdgeWt(w);
V[G.edge_v2(w)] = v;
H.insert( new ElemItem<EdgeElem>
( new EdgeElem(w, -1 * G.getEdgeWt(w))));
}
}
H.printHeap();
}
}
由于在前面章节中我们只讨论了最大堆,这里没有为PrimPQ算法特别设计最小堆,而是在函数中对最大堆来稍作改变来实现最小堆的功能:在向堆中添加边信息时,先将边的权值取相反数。
图中边的信息包括边的源点、终点和权值,由于基于连接表的图数据结构中没有这样的边数据结构,这里重新设计了边数据结构作为堆中元素项。其设计如下:
* 继承Comparable接口的EdgeElem类,其中包含一条边和这条边的权值
*/
public class EdgeElem implements Comparable{
Edge e;
int wt;
// 构造函数
public EdgeElem(Edge _e, int _wt){
e = _e;
wt = _wt;
}
// 获取边的起点
public int get_v1(){
return e.get_v1();
}
// 获取边的终点
public int get_v2(){
return e.get_v2();
}
// 获取边的权值
public int get_wt(){
return wt;
}
// 比较函数,比较对象为PrinElem的边的权值
public int compareTo(Object o) {
EdgeElem other = (EdgeElem)o;
if(wt > other.wt) return 1;
else if(wt == other.wt) return 0;
else return -1;
}
// 便于显示,返回边信息
public String toString(){
return "(" + e.get_v1() + ", "
+ e.get_v2() + "), " + wt;
}
}
这里不对算法的详细过程进行分析,通过示示例程序并跟踪堆中元素项的变化来进行解释,读者可以自行分析算法流程。示例程序使用的图为例。示例程序如下:
public static void main(String args[]){
GraphLnk GL =
Utilities.BulidGraphLnkFromFile("Graph\\graph7.txt");
MinimumSpanningTree MSTex = new MinimumSpanningTree(GL);
MSTex.PrimPQ(0);
MSTex.mst.ford_print_tree();
System.out.println("各顶点的父节点:");
for( int i = 0; i < MSTex.V.length; i++){
System.out.print(MSTex.V[i] + ", ");
}
System.out.println("\n各顶点距其父节点距离:");
for( int i = 0; i < MSTex.D.length; i++){
System.out.print(( int)(MSTex.D[i]) + ", ");
}
}
}
堆中元素旋转90度分层打印:
(0, 1), -4
(0, 7), -8
堆中元素旋转90度分层打印:
(0, 7), -8
堆中元素旋转90度分层打印:
(0, 7), -8
(1, 2), -8
堆中元素旋转90度分层打印:
(1, 2), -8
堆中元素旋转90度分层打印:
(7, 8), -7
(7, 6), -1
(1, 2), -8
堆中元素旋转90度分层打印:
(7, 8), -7
(1, 2), -8
堆中元素旋转90度分层打印:
(7, 8), -7
(6, 5), -2
(6, 8), -6
(1, 2), -8
堆中元素旋转90度分层打印:
(7, 8), -7
(6, 8), -6
(1, 2), -8
堆中元素旋转90度分层打印:
(7, 8), -7
(5, 4), -10
(5, 2), -4
(5, 3), -14
(6, 8), -6
(1, 2), -8
堆中元素旋转90度分层打印:
(7, 8), -7
(6, 8), -6
(5, 3), -14
(1, 2), -8
(5, 4), -10
堆中元素旋转90度分层打印:
(7, 8), -7
(6, 8), -6
(2, 3), -7
(2, 8), -2
(5, 3), -14
(1, 2), -8
(5, 4), -10
堆中元素旋转90度分层打印:
(7, 8), -7
(2, 3), -7
(6, 8), -6
(5, 3), -14
(1, 2), -8
(5, 4), -10
堆中元素旋转90度分层打印:
(7, 8), -7
(2, 3), -7
(6, 8), -6
(5, 3), -14
(1, 2), -8
(5, 4), -10
堆中元素旋转90度分层打印:
(7, 8), -7
(2, 3), -7
(5, 3), -14
(1, 2), -8
(5, 4), -10
堆中元素旋转90度分层打印:
(5, 3), -14
(7, 8), -7
(1, 2), -8
(5, 4), -10
堆中元素旋转90度分层打印:
(5, 3), -14
(7, 8), -7
(3, 4), -9
(1, 2), -8
(5, 4), -10
堆中元素旋转90度分层打印:
(5, 3), -14
(1, 2), -8
(3, 4), -9
(5, 4), -10
堆中元素旋转90度分层打印:
(5, 3), -14
(3, 4), -9
(5, 4), -10
堆中元素旋转90度分层打印:
(5, 4), -10
(5, 3), -14
堆中元素旋转90度分层打印:
(5, 4), -10
(5, 3), -14
堆中元素旋转90度分层打印:
(5, 3), -14
堆中元素旋转90度分层打印:
9 节点,前序遍历打印:
|—— 0.0(0)
|—— 4.0(1)
|—— 8.0(7)
|—— 1.0(6)
|—— 2.0(5)
|—— 4.0(2)
|—— 2.0(8)
|—— 7.0(3)
|—— 9.0(4)
各顶点的父节点:
-1, 0, 5, 2, 3, 6, 7, 0, 2,
各顶点距其父节点距离:
0, 4, 4, 7, 9, 2, 1, 8, 2,
程序打印结果的第一部分为堆中边的动态变化情况;第二部分为生成的MST,其中根节点为算法的起始顶点;最后一部分表示的是各顶点的在MST中的父节点以及与父节点形成的边的权值。
3 Kruskal算法
Prim算法和基于优先队列的Prim算法的思路都是通过一次找出一条边添加到MST中,其中每一步都是要找到一条新的边并且关联到不断增长的当前MST。Kruskal算法也是一次找到一条边来不断构建MST,但是与Prim算法不同的是,它要找到 连接两棵树的一条边,这两棵树处于一个MST子树的分离的森林中,其中MST子树将不断增长。
算法由一个包括N棵(单个顶点组成的)树的森林开始。然后持续完成合并两棵树的操作(使用最短的边连接它们),直至只剩下一棵树,这棵树就是最终的MST树。这一过程等效于:首先将每个顶点各自划分至一个“等价类”,共N个等价类,每次选择最短的边将等价类进行合并,直至只剩下一个等价类为止。
为保证连接等价类边的权值最短,算法首先对图中所有边按照权值进行排序。按权值由小到大一次选择边,如果边的两顶点分别属于不同的等价类,则将这条边添加到MST并将这对顶点所属的等价类合并。本节最后一部分将介绍的UnionFind类将是一个理想的数据结构,可以实现等价类的合并(Union)并判断两个顶点是否属于同一个等价类(Find)。
基于以上的描述,Kruskal算法实现如下:
* Krustral算法获取最小支撑树;算法借助UnionFind类
*/
public void Krustral(){
int nv = G.get_nv();
int ne = G.get_ne();
// 获取图上的每一条边,并将边按照权值由大到小排序
ITEM[] E = Utilities.GetEdgeSort(G);
// 集合形式的等价类
UnionFind UF = new UnionFind(nv);
// 待返回的EdgeElem数组
R = new EdgeElem[nv];
int r = 0;
for( int i = 0, k = 1; i < ne && k < nv; i++){
// 获取一条边
EdgeElem pe = (EdgeElem)(E[i].getElem());
int v1 = pe.get_v1();
int v2 = pe.get_v2();
// 如果这条边的两个顶点不在同一个等价类中
if(UF.find(v1) != UF.find(v2)){
// 则将这两个顶点合并,
UF.union(v1, v2);
System.out.println(UF.toString());
// 并将这条边添加到EdgeElem数组中
R[r++] = pe;
}
}
}
算法中调用函数GetEdgeSort获取图中所有边,并按照权值有小到大进行排序。GetEdgeSort函数首先将图中所有边取出,并以EdgeElem类的对象形式放置到ITEM类型的数组E中;然后调用第章中的任意一种排序算法对E中元素进行排序,其中EdgeElem类继承的copmareTo函数比较的是两个边对象的权值。这里选择快速排序算法,经过快速排序后E数组中的边按照权值有小到大顺序排列。算法实现过程如下:
* 获取图中所有边,并将这些边按照权值由大到小排序;
* @param G 函数输入为图G
* @return 返回为ITEM数组,每个元素为EdgeElem
* 对象,元素按照权值排序;
*/
public static ITEM[] GetEdgeSort(Graph G){
if(G == null) return null;
// 首先将所有边存至ITEM数组
int ne = G.get_ne();
int nv = G.get_nv();
ITEM[] E = new ITEM[ne];
int edge_cnt = 0;
for( int i = 0; i < nv; i++){
for(Edge e = G.firstEdge(i); G.isEdge(e); e = G.nextEdge(e)){
E[edge_cnt++] = new ITEM( new EdgeElem(e, G.getEdgeWt(e)));
}
}
// 将ITEM数组排序,这里采用快速排序
Sort st = new Sort();
st.quicksort(E, 0, E.length - 1);
// 返回ITEm数组
return E;
}
图(1~8)逐步实例了Kruskal算法的操作,从不连通的子树森林逐步演化为一棵树。边按其长度的顺序添加到MST中,所以组成此森林的顶点相互之间都通过相对短的边连接。
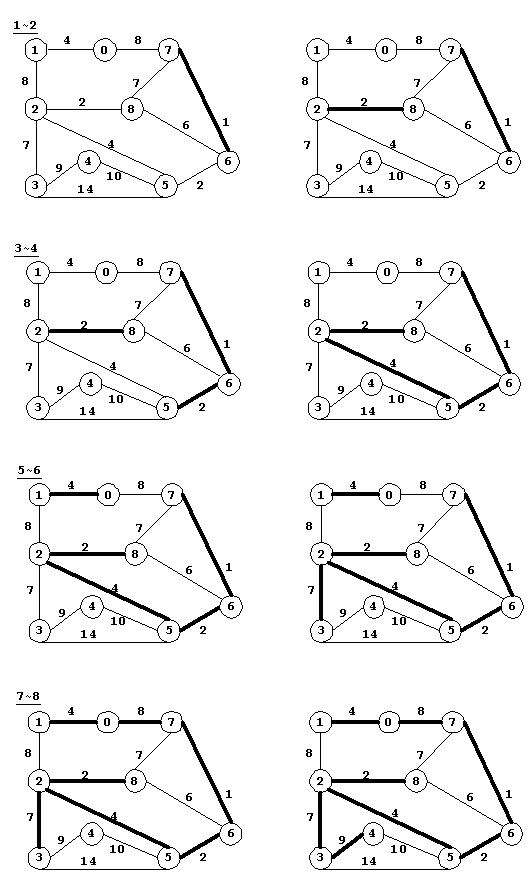
以上图为例调用Krustral函数,并跟踪UnionFind对象中等价类的变化过程。实例程序如下:
public static void main(String args[]){
GraphLnk GL =
Utilities.BulidGraphLnkFromFile("Graph\\graph7.txt");
MinimumSpanningTree MSTex = new MinimumSpanningTree(GL);
MSTex.Krustral();
MSTex.mst.ford_print_tree();
System.out.println("MST各条连接边为:");
for( int i = 0; i < MSTex.R.length; i++){
System.out.println(MSTex.R[i]);
}
}
}
0. -1, 1. -1, 2. -1, 3. -1, 4. -1, 5. -1, 6. -2, 7. 6, 8. -1,
0. -1, 1. -1, 2. -2, 3. -1, 4. -1, 5. -1, 6. -2, 7. 6, 8. 2,
0. -1, 1. -1, 2. -2, 3. -1, 4. -1, 5. 6, 6. -2, 7. 6, 8. 2,
0. -1, 1. -1, 2. 6, 3. -1, 4. -1, 5. 6, 6. -3, 7. 6, 8. 2,
0. 1, 1. -2, 2. 6, 3. -1, 4. -1, 5. 6, 6. -3, 7. 6, 8. 2,
0. 1, 1. -2, 2. 6, 3. 6, 4. -1, 5. 6, 6. -3, 7. 6, 8. 6,
0. 1, 1. 6, 2. 6, 3. 6, 4. -1, 5. 6, 6. -3, 7. 6, 8. 6,
0. 6, 1. 6, 2. 6, 3. 6, 4. 6, 5. 6, 6. -3, 7. 6, 8. 6,
MST各条连接边为:
(6, 7), 1
(2, 8), 2
(6, 5), 2
(5, 2), 4
(1, 0), 4
(3, 2), 7
(0, 7), 8
(3, 4), 9
结果第一部分为等价类变化过程,第二部分为MST中添加边的顺序。对等价类的显示结果这里先简要解释,详细分析请参见本节UnitFind部分。以结果中第6行为例进行解释:
0. 1,1. -2,2. 6,3. 6,4. -1,5. 6,6. -3,7. 6,8. 6,
其中“.”之前前的数值表示顶点号;之后的数值表示了与该顶点属于同一个等价类的另一顶点,如果该值为负数,表示该顶点为所属等价类中的根。例如,顶点0对应值为1,而顶点1对应值为-2,则顶点0和1属于同一个等价类;顶点2, 3, 5, 7, 8对应值都为6,所以顶点2, 3, 5, 6, 7, 8属于同一个等价类。对应个顶点链接图为图中(6)。
4. Boruvka算法
Boruvka算法是MST算法中最为古老的算法。类似于Kruskal算法,Bruvka算法也要向MST子树的森林添加边来构建MST;但是这是分步完成,每一步都增加多条MST边。在每一步中,会连接每一棵MST子树与另一棵子树的最短边,再将所有这样的边都增加到MST中。
本算法同样借助于UnionFind类。首先维护一个顶点索引数组,它可为各个MST子树找出最近的邻居。其次对图中每条边进行以下操作:
l 如果此边链接了同一子树上的两个顶点,则将其删除;
l 否则,检查此边所连接的两个子树之间的最近邻居距离,如果有则更新此距离。
遍历操作图中所有顶点后,最近邻居数组中则有了链接子树所需的边的信息。对于每个顶点索引,要完成一个合并操作(Union)使它与其最近邻居相连接。在下一步中,去除目的连接的MST子树中链接其他顶点对的所有更长边。算法实现如下:
* Boruvka 算法求解最小支撑树
* */
public void Boruvka(){
int nv = G.get_nv();
int ne = G.get_ne();
// 获取图上的每一条边
EdgeElem[] E = Utilities.GetEdge(G);
EdgeElem[] B = new EdgeElem[nv];
// 集合形式的等价类
UnionFind UF = new UnionFind(nv);
// 待返回的EdgeElem数组
R = new EdgeElem[nv];
int r = 0;
int N = 0;
// 权值为无穷大的边
EdgeElem _z = new EdgeElem( null,
Integer.MAX_VALUE);
// 对每一个子树
for( int e = ne; e != 0; e = N){
System.out.print("h-\t");
System.out.println(UF.toString());
int h, i, j;
// 权值初始化为 oo
for( int t = 0; t < nv; t++)
B[t] = _z;
// 对每一条边
for(h = 0, N = 0; h < e; h++){
EdgeElem pe = E[h];
// 获取边的起点和终点
i = UF.find(pe.get_v1());
j = UF.find(pe.get_v2());
// 起点和终点如果在同一个等价类中,则跳出本次循环
if(i == j)
continue;
// 更新两棵树之间的最近距离
if(pe.get_wt() < B[i].get_wt())
B[i] = pe;
if(pe.get_wt() < B[j].get_wt())
B[j] = pe;
// N表示的是当前的子树个数
E[N++] = pe;
}
// 对MST中每条边
for(h = 0; h < nv; h++){
// B[h]是第h个顶点与其它树之间的最近距离的边
if(B[h] != _z
// 如果B[h]的起点和终点不在同一个等价类中
&& UF.find(B[h].get_v1())
!= UF.find(B[h].get_v2())){
// 将起点和终点放置到同一个等价类中
UF.union(B[h].get_v1(), B[h].get_v2());
// 并将这条边添加到EdgeElem数组中
R[r++] = B[h];
}
}
}
}
函数中,E数组中首先保存途中所有顶点,调用函数GetEdge实现。数组B即为用于各个子树找出最近的邻居的顶点索引数组。算法初始状态下每个顶点分别属于不同等价类,然后按照上面算法描述中的方法找出各子树之间的最近连接边。
图(1~8)显示了算法的过程,其中(1~6)为第一次遍历过程,并得到三个子树形成的森林;(7~8)为第二次遍历过程,得到最终的最小支撑树。算法过程中跟踪每次遍历后等价类的变化。
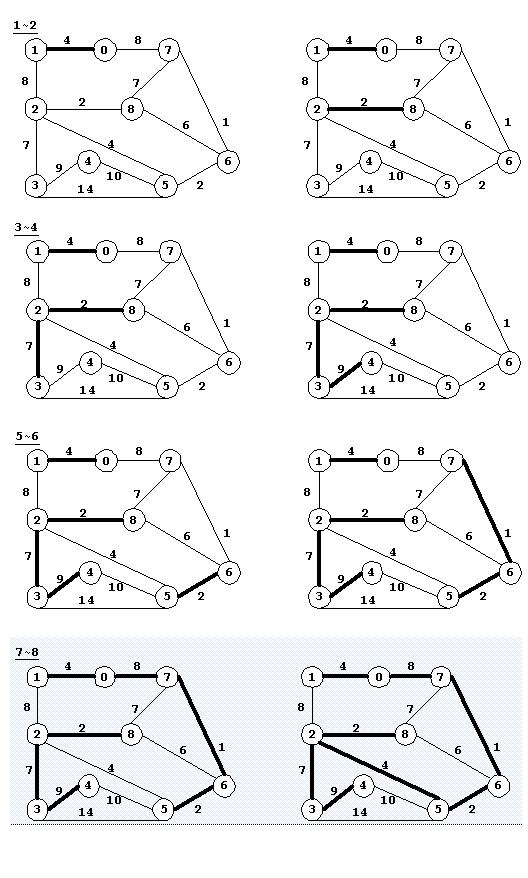
以上图为例,对算法进行测试,实例程序如下:
public static void main(String args[]){
GraphLnk GL =
Utilities.BulidGraphLnkFromFile("Graph\\graph7.txt");
MinimumSpanningTree MSTex = new MinimumSpanningTree(GL);
MSTex.Boruvka();
System.out.println("MST各条连接边为:");
for( int i = 0; i < MSTex.R.length; i++){
System.out.println(MSTex.R[i]);
}
}
}
0. -1, 1. -1, 2. -1, 3. -1, 4. -1, 5. -1, 6. -1, 7. -1, 8. -1,
0. -2, 1. 0, 2. -2, 3. 2, 4. 2, 5. -2, 6. 5, 7. 5, 8. 2,
0. -3, 1. 0, 2. 0, 3. 2, 4. 2, 5. 0, 6. 5, 7. 5, 8. 2,
MST各条连接边为:
(0, 1), 4
(2, 8), 2
(2, 3), 7
(3, 4), 9
(5, 6), 2
(6, 7), 1
(0, 7), 8
(2, 5), 4
UnionFind类
UnionFind(合并查找)类可以实现等价类描述。假设一组元素V,其中元素分为n(n ≤ |V|)等价类C1, C2, …, Cn。等价类满足一下性质:
l 每一个元素只能属于一个等价类;
l 等价类的同属关系具有传递性。
对于第二个性质,设顶点vi与vj属于同一等价类,顶点vk与vj属于同一等价类,则顶点vi和vk与vj都属于同一等价类。
这里我们关心两个等价类的合并(Union)和任意元素所属等价类名称的返回(Find)。这里我们定义等价类的名称为等价类中某个特定的元素,由于每个元素只可能属于一个等价类,所以每个等价类的名称一定是唯一的,我们称之为这个等价类的根。合并两个等价类时,可以分别指定两个等价类中任意元素,然后将它们合二为一。
类的实现如下:
/**
* 等价关系(等价类)ADT的实现,这里的等价类表示数组中元素的是否是同一类。
* 数组array表示的是下标序号关联。
* */
public class UnionFind {
private int[] array;
/**
* 构造函数,参数为array的长度
* */
public UnionFind( int numElements) {
array = new int [numElements];
// 数组中数值全为 -1
for ( int i = 0; i < array.length; i++) {
array[i] = -1;
}
}
/**
* union() 将两个集合合并为同一个集合,具体来说是将
* 第一个集合的下标与第二个集合的下标合并到一个集合中。
* @param root1 第一个集合中的任意一个下标.
* @param root2 第二个集合中的任意一个下标.
* 如果root1和root2分别不是两个集合的根,则首先将他们
* 的根求出来
* */
public void union( int root1, int root2) {
// 如果root1和root2分别不是两个集合的根,
// 则首先将他们的根求出来
root1 = find(root1);
root2 = find(root2);
// 如果root2更高,则将root2设为合并后的根
if (array[root2] < array[root1]) {
array[root1] = root2;
}
else {
// 如果一样高,减小其中一个的高度
if (array[root1] == array[root2]) {
array[root1]--;
}
// 一样高或者root1更高,则将root1设为合并后的根
array[root2] = root1;
}
}
/**
* find() 寻找输入下标所在的集合的集合名
* @param x: 输入下标
* @return : 集合名
* */
public int find( int x) {
// x是根,直接返回
if (array[x] < 0) {
return x;
}
else {
/* 递归寻找x的根,在递归过程中将压缩x的索引深度,
* 使得array[x]中保存根节点的下标 */
array[x] = find(array[x]);
return array[x]; // 返回根节点
}
}
/**
* 返回所有的等价类
*/
public String toString(){
String s = "";
for( int i= 0; i < array.length; i++){
s += i+". "+array[i] + ",\t";
}
return s;
}
}
其中似有成员为整型数组,数组下标对应实际元素的序号。例如array[i]的值包含第i个元素所属的等价类。find函数是递归函数,充分利用等价类的第二个性质。对于元素i,array[i]=j,包含两种情况:
l 如果j<0,则说明第i个元素为等价类的根,该等价类的名为i,则返回i;
l 如果j>0,则说明第i个元素与第j个元素属于同一个等价类,则递归调用函数find返回j的等价类名称,递归调用直至满足上一情况为止。
union函数将两个等价类合并,只需要分别指定两个等价类中的任意元素i, j,
l 如果这两个元素分别是等价类的名,则将array[j]←i;
l 否则,首先调用函数find找到两个等价类的名称,然后再合并。
在本节讨论的Kruskal算法和Boruvka算法都利用了UnionFind类的union函数和find函数,读者可自行体会函数的功能。





















 819
819











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








