最近看了张学工老师的《关于统计学习理论与支持向量机》和Vapnik的《Support Vector Networks》两篇文章。张学工老师是国内接触SVM比较早的学者,他的这篇文章算是支持向量机的一个综述;而Vapnik先生是SVM的发明者,SVM大牛中的大牛。他的这篇文章据说是支持向量机的第一篇论文。
我看文献的习惯是先找一篇国内比较好的综述进行阅读,然后从这篇文章中去找相应的英文文献进行阅读。毕竟现在学术界很多新的理论、技术都来源于西方,因此,要想快速的掌握某个理论及其最新进展,阅读英文文献必不可少;如果想快速形成对所研究事物的初步看法并且想知道应该去找哪些英文文献来阅读的话,阅读国内的综述性文章也很必要。
支持向量机其实是分类思想发展的必然结果,可以说,从Fisher先生1936年提出Fisher线性判别而导致模式分类技术的诞生开始,就已经注定了终有一天,支持向量机SVM会出现。SVM是一种有监督的机器学习,它的目的是根据训练集给出的样本来求取对系统输入输出关系的估计,当然,这种估计越准确越好。下面就是学习机的一个基本模型。
(1)线性判别函数
如同上一篇所讲的,对于一个线性可分的两类问题,可以定义一个表达式
其中x是d维特征向量,w是权向量,![]() 是阈值权。则可以采用如下的决策规则:
是阈值权。则可以采用如下的决策规则:
分类策略如下:
事实上,g(x)定义了一个决策面,也叫分类面,将![]() 和
和![]() 中的样本区分开来。通过上一篇中的证明,我们知道g(x)定义的超平面把特征空间分成了两个决策区域,超平面方向由
中的样本区分开来。通过上一篇中的证明,我们知道g(x)定义的超平面把特征空间分成了两个决策区域,超平面方向由![]() 决定,位置由阈值权
决定,位置由阈值权![]() 决定,判别函数正比于x到超平面的代数距离,即
决定,判别函数正比于x到超平面的代数距离,即 。
。
(2)广义线性判别函数
线性判别函数虽然简单,但是局限性很大,因为实际问题往往都非常复杂,不可能都是非线性这么简单。因此,对于非线性问题,当然要建立非线性判别函数了。例如对于下面的二阶问题:
如上图所示的两类问题,如果x<b或者x>a,则x属于![]() 类;如果b<x<a,则x属于
类;如果b<x<a,则x属于![]() 类。那么定义二次判别函数:
类。那么定义二次判别函数:
就可以很好地解决上面的分类问题,决策规则为:
二次判别函数可以写成:
上面的二次分类器能很好地将数据分开,但我们知道,当判别函数的阶数越高的话,整个系统就越复杂,我们可能根本无法得出这样高阶的模型。但是这里出现了一种新思想,一种对以后分类器设计影响非常大的思想,那就是广义线性判别函数。
广义线性判别是找到一种适当的![]() 映射,则可以把二次判别函数化为z的线性函数
映射,则可以把二次判别函数化为z的线性函数
式中:
广义线性判别函数的一般表达式:
其中
![]() 叫做增广样本向量,a叫做增广权向量,它们是
叫做增广样本向量,a叫做增广权向量,它们是![]() 维向量。因此这是一种将低维上的非线性问题转化到高维上的线性问题的思想。
维向量。因此这是一种将低维上的非线性问题转化到高维上的线性问题的思想。
(3)最优分类面
前面已经说过,线性判别函数或者广义线性判别函数实际上定义了一系列分类面,用来将训练样本无错误地分开。如下图所示:
要想将图中的两个类分开,可以有很多分类面H,但是,究竟哪个面最好呢?图中的H3也能将两类分开,难道我们要选它作为分类面吗?
SVM就是从线性可分情况下的最优分类面(Optimal Hyperplane)提出的。如上图所示,考虑两类线性可分情况,H为把两类没有错误地分开的分类线,![]() ,
,![]() 分别为过各类样本中离分类线最近且平行于分类线的直线,
分别为过各类样本中离分类线最近且平行于分类线的直线,![]() 和
和![]() 之间的距离叫做两类的分类间隔。
之间的距离叫做两类的分类间隔。
所谓最优分类面就是要求分类面不但能将两类无错误地分开,而且要使两类的分类间隔最大。很显然,上图中的H3不是一个最优分类面。
设线性可分样本集为![]() 是类别标号。d维空间中线性判别函数的一般形式是
是类别标号。d维空间中线性判别函数的一般形式是![]() ,分类面方程为:
,分类面方程为:
将判别函数归一化,则分类间隔变为 (推导过程见前一节),因此要使间隔最大,则要使
(推导过程见前一节),因此要使间隔最大,则要使 最小或者
最小或者 最小。而要求对所有样本正确分类,则要满足:
最小。而要求对所有样本正确分类,则要满足:
满足上面条件且使 最小的分类面就是最优分类面。过两类样本中离分类面最近的点且平行于最优分类面的超平面
最小的分类面就是最优分类面。过两类样本中离分类面最近的点且平行于最优分类面的超平面![]() 和
和![]() 上的训练样本就是使(8)中等号成立的样本,叫做支持向量。所以对于支持向量这个名字我们要注意,它指的还是训练集中的样本,只不过是特殊的样本。
上的训练样本就是使(8)中等号成立的样本,叫做支持向量。所以对于支持向量这个名字我们要注意,它指的还是训练集中的样本,只不过是特殊的样本。
最优分类面问题可以转化成下面的约束优化问题,即在(8)的约束下求函数
其中![]() 为Lagrange系数,对w和b求Lagrange函数的最小值。
为Lagrange系数,对w和b求Lagrange函数的最小值。
通过求偏导和对偶原理,上面的问题转化为在约束
从(13)中可以看出,最优分类面的权系数向量是训练集样本向量的线性组合。当然,一旦权向量出来了,b就很好求了,只要将支持向量代入表达式(8)使等号成立即可。这是一个约束条件下的二次寻优问题,存在唯一解。根据Kuhn-Tucker条件,这个优化问题必须满足
最终得到的最优分类函数可以用一个符号函数来表示:
后记:这里只是简单讨论最简单的支持向量机的诞生过程,支持向量机是统计学习理论发展的集大成,具有很多新的特点,接下来将着重讲述在简单线性可分支持向量机基础上的扩展。

















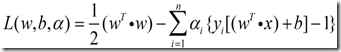



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








