PAT甲级——A1086 Tree Traversals Again

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

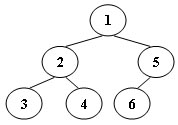
Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2 lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1

 1 //这道题就是已知前序和中序遍历，得到后序遍历
 2 //push为前序遍历，pop为中序遍历
 3 #include <iostream>
 4 #include <vector>
 5 #include <stack>
 6 #include <string>
 7 using namespace std;
 8 int N;
 9 vector<int>preOrder, inOrder, posOrder;
10 struct Node
11 {
12     int val;
13     Node *l, *r;
14     Node(int a = 0) :val(a), l(nullptr), r(nullptr) {};
15 };
16 Node* createTree(int preL, int preR, int inL, int inR)
17 {
18     if (preL > preR)
19         return nullptr;
20     Node* root = new Node(preOrder[preL]);
21     int i;
22     for (i = inL; i <= inR; ++i)//找到根节点
23         if (inOrder[i] == preOrder[preL])        
24             break;
25     int num = i - inL;
26     root->l = createTree(preL + 1, preL + num, inL, i - 1);
27     root->r = createTree(preL + num + 1, preR, i + 1, inR);
28     return root;
29 }
30 void posOrderTree(Node *root)
31 {
32     if (root == nullptr)
33         return;
34     posOrderTree(root->l);
35     posOrderTree(root->r);
36     posOrder.push_back(root->val);
37 }
38 int main()
39 {
40 
41     cin >> N;
42     string str;
43     stack<int>s;
44     int a;
45     for (int i = 0; i < 2*N; ++i)
46     {
47         cin >> str;
48         if (str == "Push")
49         {
50             cin >> a;
51             s.push(a);
52             preOrder.push_back(a);
53         }
54         else
55         {
56             inOrder.push_back(s.top());
57             s.pop();
58         }
59     }
60     Node* root = createTree(0, N - 1, 0, N - 1);
61     posOrderTree(root);
62     for (int i = 0; i < N; ++i)
63         cout << posOrder[i] << (i == N - 1 ? "" : " ");
64     return 0;
65 }

 

转载于:https://www.cnblogs.com/zzw1024/p/11337914.html