HDU-5532//2015ACM/ICPC亚洲区长春站-重现赛-F - Almost Sorted Array/,哈哈，水一把区域赛的题~~...

最新推荐文章于 2019-05-29 10:48:00 发布

weixin_30650859

最新推荐文章于 2019-05-29 10:48:00 发布

阅读量122

点赞数

原文链接：http://www.cnblogs.com/nyist-TC-LYQ/p/7208253.html

版权

F - Almost Sorted Array

Time Limit:2000MS Memory Limit:262144KB 64bit IO Format:%I64d & %I64u

Submit Status Practice HDU 5532

Description

We are all familiar with sorting algorithms: quick sort, merge sort, heap sort, insertion sort, selection sort, bubble sort, etc. But sometimes it is an overkill to use these algorithms for an almost sorted array.

We say an array is sorted if its elements are in non-decreasing order or non-increasing order. We say an array is almost sorted if we can remove exactly one element from it, and the remaining array is sorted. Now you are given an array

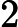
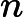, is it almost sorted?

Input

The first line contains an integer

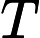indicating the total number of test cases. Each test case starts with an integer

in one line, then one line with

integers

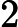
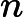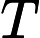
There are at most 20 test cases with

Output

For each test case, please output "`YES`" if it is almost sorted. Otherwise, output "`NO`" (both without quotes).

Sample Input

       3 3 2 1 7 3 3 2 1 5 3 1 4 1 5 
     

Sample Output

       YES YES 
      NO 

在virtual judge上无意点了个开放的专题，竟然是区域赛的题，而且竟然是学长拉的题，奈何我这种大一菜鸟神马都不会，做那个求异或最大值的用三层for循环直接超时，题目明明规定的是9000ms,学长说现场赛的话还可以暴力过，但重现赛就没那么好过了，看到他们都A了这个题，于是也跟榜做做这个题；

题意并不难理解，只不过出题人喜欢拐弯抹角，两种状态：一种已经被排好序，我们就称之为标准态吧，另一种是只能移除一个而形成标准态；

我们来分析第一种标准态：数组元素呈非递增或非递减态排布；注意这个“或”字，或非递增或非递减，即是说既可以是递增也可以是递减，出题人在这里卡了一下，不过，我相信对于能参加区域赛的大神来说并无障碍；

分析好了题意就可以想思路了，题目求的是给定一个数组，能否只移除一个元素使它变成标准态，这里还需要注意的是如果原数组就是标准态，那么不管移除哪个都仍是标准态；所以我们只需要考虑原数组屏蔽某个元素后是否是标准态即非单调递增或非单调递减的状态；说白了，就是求这个数组的非单调递增或非单调递减的元素个数（长度）是否为n或n-1(假设给定数组的长度为n);

所以用二分求出非单调递增和非递减的长度，可以有相等的，不一定是单调的，这里也是一个坑点；只需把二分算法中的大于改成大于等于就好了；

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=100000+10;
int  a[N],b[N];
int s(int num,int l,int h)
{
    int mid;
    while(l<=h)
    {
        mid=(l+h)/2;
        if(num>=b[mid])
            l=mid+1;
        else h=mid-1;
    }
    return l;
}
int dp1(int n)//求非单调递减的序列长度；下面同理；
{
    int i,len,pos;
    b[1]=a[1];
    len=1;
    for(i=2; i<=n; i++)
    {
        if(a[i]>=b[len])//可以等，下面同理；
        {
            len=len+1;
            b[len]=a[i];
        }
        else
        {
            pos=s(a[i],1,len);
            b[pos]=a[i];
        }
    }
    return len;
}
int dp2(int n)
{
    int i,len,pos;
    b[1]=a[n];
    len=1;
    for(i=n-1; i>=1; i--)
    {
        if(a[i]>=b[len])
        {
            len=len+1;
            b[len]=a[i];
        }
        else
        {
            pos=s(a[i],1,len);
            b[pos]=a[i];
        }
    }
    return len;
}
int main()
{
    int t,n,i;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        for(i=1; i<=n; i++)
             scanf("%d",&a[i]);

        int x1=dp1(n);
        int x2=dp2(n);
       if(x1==n||x1==n-1||x2==n||x2==n-1)//等于n说明已经是标准态，否则可以移除一个；
        printf("YES\n");
       else
        printf("NO\n");
//        printf("%d %d\n",x1,x2);
    }
    return 0;
}

代码写出来也不是很难，关键就是我们分析题意，搞清思路，然后代码实现；

转载于:https://www.cnblogs.com/nyist-TC-LYQ/p/7208253.html