学习算法导论:
对于矩阵A(2,3)*B(3,5)其运算次数为2*3*5;
对于矩阵A(2,3)*B(3,5)*C(5,4)存在两种运算结合顺序,运算次数分别为2*3*5+2*5*4=70以及3*5*4+2*3*4=84,显然运算次数不同。
给定一系列矩阵A1A2A3...An,由于矩阵乘法符合结合律,所以不同的结合顺序,运算效率完全不同,求出运算效率最高的结合顺序。
枚举法:
假设P(n)为一系列n个矩阵可能的括号化方案数,则
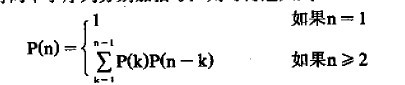
可得到

动态规划学习:
(1)寻找最优子结构
记Ai...j表示乘积AiAi+1...Aj的值,则A1...n的最优括号化将乘积在Ak和Ak+1之间分开(1<=k<n)。即对于某个k值,我们先计算A1...k和Ak+1...n,然后再把这两个乘积的值相乘即为最终的解。由此最优括号化的代价就是计算A1...k和Ak+1...n的代价之和,然后加上这两者相乘的代价。
注:A1...k必须也保证是最优括号化,因为假设存在一种代价更小的括号化,我们可以以此方案来取代当前的这个方案,由此计算出来的A1...n的代价还小于之前的那个最优代价,产生矛盾。同理Ak+1...n也必须是最优括号化。(剪贴法证明)
由此可得,矩阵链乘法问题的最优解包含了其子问题的最优解。
最优子结构在问题域中以两种方式变化:
1.有多少个子问题被使用在原问题的一个最优解中;
2.在决定最优解中使用哪些子问题时有多少个选择。
总结:
在确定一个给定的问题时,首先要做出选择,在已知这个选择后,要确定哪些子问题会随之发生。(选择,子问题)
(2)利用子问题(必须相互独立)最优解递归定义一个最优解
定义m[i,j]为Ai...j的最优代价(1<=i,j<=n),则可得出
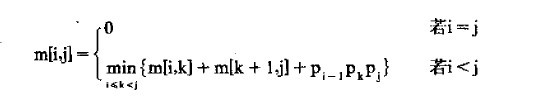
(3)计算最优解
算法方案如下:

注:s[i][j]为计算m[i][j]最优括号化中的k
计算顺序如下图:
为了计算m[i][j],则以此i,j为中心建立坐标系,第三象限中的值必须全部都已经计算出来。所以可按照上图所给出的计算顺序,最终可保证计算出m[1][n]。
算法复杂度估算:
为了计算每个m[i][j]其算法复杂度为O(j-i),计算m[i][j]的个数大致为O(n*n),所以最终的算法复杂度应为O(n*n*n)
总结:
时间复杂度为子问题总个数和每个子问题中有多少种选择来决定。
问题解决的代价通常是子问题的代价加上选择本身带来的开销。两种确定最优解的方法:自底向上的动态规划算法和自顶向下的备忘递归算法。
因此采用自底向上的动态规划计算最优解时,首先要得到子问题的最优解,解决了子问题以后,然后才能找到问题的一个最优解;若是采用自顶向下的递归算法,则需要设置一个备忘录(当然采用自底向上的DP时必须开辟一定的空间以保存子问题的最优解),初始时备忘录上的各个元素加上标记NIL,代表未确定出来,然后使用递归求解时,每当碰见子问题为NIL时,则求解它,否则由备忘录中取出来(时间复杂度为常数级)。
通常一个自底向上的DP要比一个自底向下的备忘录递归算法要好处一个常数因子,因为前者无需递归的代价,而且维护表格的开销也小一点。
(4)构造最优解(计算出最优解的求解过程)
上一步已经求出了最优括号化的代价,因此这一步应该得出如何得出这个最优方案。
s[i][j]已经给出了计算m[i][j]的最优分隔值。所以可由递归算法得出最优括号化方案。

动态规划总结:
动态规划的标志:
(1)最优子结构:
寻找最优子结构,问题的一个接可以是做一个选择,比如上例,选择一个下标在该位置分裂矩阵链。我们不必关心这个选择,尽管假设它是已知的,即已知的是一个可以导致最优解的选择。在做出这个选择时会得到一个或多个有待解决的子问题。因此分析问题的代价时,通常是子问题的代价加上做出选择的开销。
(2)重叠子问题:
子问题的空间要很小,也就是用来求解原问题的递归算法可重复地求同样的子问题,而不是总在产生新的子问题。当一个递归算法不断的调用同一子问题时,我们说该最有问题包含“重叠子问题”。
由于递归算法总是重复的计算子问题,因此可能会导致算法的复杂度为指数级,这显然不是我们所希望看到的。因此动态规划引入备忘录,总是充分的利用重叠子问题,每个子问题只是求解一次,然后把解保存在一个需要时就可以查看的表中,每次查表的时间为常数。表格化的解法把一个指数时间里的递归算法降为了多项式时间的算法。
动态规划的步骤:
首先必须寻找最优解的最优子结构,这是动态规划应用的标记之一。做出一个选择,将问题分解成不同的子问题(子问题必须独立,不然动态规划算法会失效)。通过建立子问题的最优解,就可以建立原问题某个实例的一个最优解。
其次根据这个最优子结构寻找最优解的递归式。
最后是程序设计的问题,即从此递归式出发,然而运用递归算法会存在大量的重复计算,因为存在大量的重叠子问题(适用于动态规划求解最优化问题的第二个标志),所以必须引入备忘录,将指数级的时间降为多项式时间。设计的方法有两种自底向上和自顶向下。前者较后者高效,一般会多出一个常数因子。
参考文献:
[1]算法导论
附录:
矩阵链乘法代码
// array_multiply_own.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <stdio.h>
#include <string.h>
#include <vector>
using namespace std;
const int MAX = 0x7fffffff;
const int ROW_MAX = 103;
const int COLUMN_MAX = 103;
const int p_max = 13;
int m[ROW_MAX][COLUMN_MAX], s[ROW_MAX][COLUMN_MAX];
int p[p_max];
int p_length;
class Matrix{
public:
int row, column;
vector<vector<int> > arr;
Matrix operator=(Matrix ma){
row = ma.row;
column = ma.column;
for(int i = 1; i <= row; i++){
for(int j = 1; j <= column; j++){
arr[i][j] = ma.arr[i][j];
}
}
}
void init(int _row, int _column, int val){
row = _row;
column = _column;
vector<int> tvec;
arr.push_back(tvec);
for(int i = 1; i <= row; i++){
vector<int> ivec;
ivec.push_back(0);
for(int j = 1; j <= column; j++){
ivec.push_back(val);
}
arr.push_back(ivec);
}
}
void print(){
for(int i = 1; i <= row; i++){
for(int j = 1; j <= column; j++){
printf("%d ",arr[i][j]);
}
printf("\n");
}
}
};
Matrix mat[p_max];
Matrix multiply(Matrix A, Matrix B){
Matrix C;
C.init(A.row, B.column, 0);
for(int i = 1; i <= A.row; i++){
for(int j = 1; j <= B.column; j++){
for(int k = 1; k <= A.column; k++){
C.arr[i][j] += A.arr[i][k] * B.arr[k][j];
}
}
}
return C;
}
void chainOrder(){
int n = p_length;
for(int l = 2; l <= n; l++){
for(int i = 1; i <= n - 1 + l; i++){
int j = i + l - 1;
m[i][j] = MAX;
for(int k = i; k <= j - 1; k++){
int temp = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if(temp < m[i][j]){
m[i][j] = temp;
s[i][j] = k;
}
}
}
}
}
Matrix chainMultiply(int low, int high){
if(high > low){
if(low != s[low][high])
printf("(");
Matrix X = chainMultiply(low, s[low][high]);
if(low != s[low][high])
printf(")");
if(high != s[low][high] + 1)
printf("(");
Matrix Y = chainMultiply(s[low][high] + 1, high);
if(high != s[low][high] + 1)
printf(")");
return multiply(X, Y);
}
else{
printf("A%d", low);
return mat[low];
}
}
int main()
{
freopen("F:\\test.txt", "r", stdin);
//freopen("F:\\output.txt", "w", stdout);
scanf("%d", &p_length);
for(int i = 1; i <= p_length; i++){
int r, col;
scanf("%d%d", &r, &col);
p[i - 1] = r;
p[i] = col;
mat[i].init(r, col, 1);
}
chainOrder();
printf("the minimum multiply times of a sequence of matrix : %d\n", m[1][p_length]);
printf("show the process of the minimum times of a sequence of matrix :\n");
Matrix res = chainMultiply(1, p_length);
printf("\n");
res.print();
return 0;
}
运算结果:
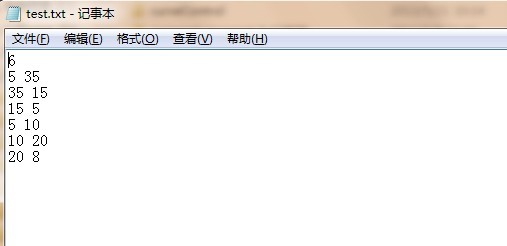
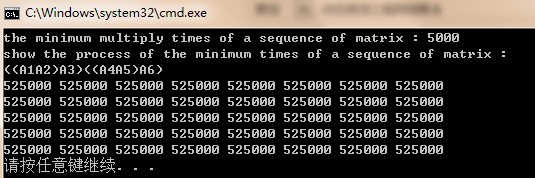






















 486
486

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








