Good Bye 2014 B. New Year Permutation 【传递闭包贪心】

最新推荐文章于 2022-06-04 00:05:30 发布

weixin_30662109

最新推荐文章于 2022-06-04 00:05:30 发布

阅读量83

点赞数

原文链接：http://www.cnblogs.com/wuyuewoniu/p/4212381.html

版权

解题思路：给出一列数an,再给出一个矩阵d[i][j],在满足d[i][j]=1的情况下，称a[i]和a[j]可以交换，问经过交换最后得到字典序最小的数列a[n]

首先是贪心的思想，大的能换就换到后面去，这样尽可能使小的在前面。

然后是判断a[i]和a[j]能不能交换，如果d[i][j]=1,表示a[i]和a[j]可直接交换如果d[i][k]=1&&d[k][j]=1,表示a[i]可以通过a[k]和a[j]交换

比如 1 7 3 4 2 5 假如 7能和4交换，4能和2交换，那么7也能和2交换

处理矩阵的时候用到了紫书中的传递闭包

for(k=1;k<=n;k++)
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
            d[i][j]=d[i][j]||(d[i][k]&&d[k][j]);

User ainta has a permutation p₁, p₂, ..., p_n. As the New Year is coming, he wants to make his permutation as pretty as possible.

Permutation a₁, a₂, ..., a_n is prettier than permutation b₁, b₂, ..., b_n, if and only if there exists an integer k (1 ≤ k ≤ n) where a₁ = b₁, a₂ = b₂, ..., a_k - 1 = b_k - 1 and a_k < b_k all holds.

As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of p_i and p_j (1 ≤ i, j ≤ n, i ≠ j) if and only if A_i, j = 1.

Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.

Input

The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.

The second line contains n space-separated integers p₁, p₂, ..., p_n — the permutation p that user ainta has. Each integer between 1and n occurs exactly once in the given permutation.

Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of thei-th line A_i, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, A_i, j = A_j, i holds. Also, for all integers i where 1 ≤ i ≤ n, A_i, i = 0 holds.

Output

In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.

Sample test(s)

input

7 5 2 4 3 6 7 1 0001001 0000000 0000010 1000001 0000000 0010000 1001000

output

1 2 4 3 6 7 5

input

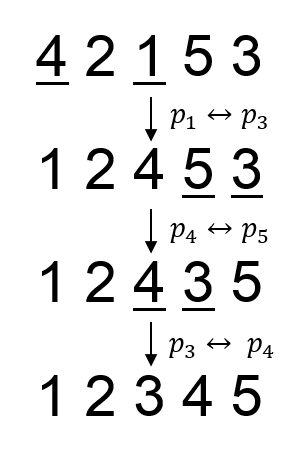
5 4 2 1 5 3 00100 00011 10010 01101 01010

output

1 2 3 4 5

Note

In the first sample, the swap needed to obtain the prettiest permutation is: (p₁, p₇).

In the second sample, the swaps needed to obtain the prettiest permutation is (p₁, p₃), (p₄, p₅), (p₃, p₄).

$\text{[math]}$

A permutation p is a sequence of integers p₁, p₂, ..., p_n, consisting of n distinct positive integers, each of them doesn't exceed n. Thei-th element of the permutation p is denoted as p_i. The size of the permutation p is denoted as n.

#include<stdio.h>
#include<algorithm>
using namespace std;
int a[1010],d[1010][1010];
char s[1020];
int main()
{
	int n,i,j,k;
	scanf("%d",&n);
	for(i=1;i<=n;i++) scanf("%d",&a[i]);
	for(i=1;i<=n;i++)
	{
		scanf("%s",&s);
		for(j=0;j<n;j++)
		{
			if(s[j]=='1')  d[i][j+1]=1;
			else  d[i][j+1]=0;
		}
	}	
	for(k=1;k<=n;k++)
		for(i=1;i<=n;i++)
			for(j=1;j<=n;j++)
			d[i][j]=d[i][j]||(d[i][k]&&d[k][j]);
	
	for(i=1;i<=n;i++)
	{
		for(j=i+1;j<=n;j++)
		{
			if(d[i][j]&&a[i]>a[j])
			swap(a[i],a[j]);
		}
	}
	for(i=1;i<n;i++)
	printf("%d ",a[i]);
	printf("%d\n",a[i]);
}

转载于:https://www.cnblogs.com/wuyuewoniu/p/4212381.html