2018北京冬令营模拟题
day1
“普及组选手做前 3 道题目,提高组选手做后 3 道题目”,所以 T1 我就不写题解了。
售票(kartomat)
试题描述
C 市火车站最近出现了一种新式自动售票机。买票时,乘客要先在售票机上输入终点名称。一共有 \(N\) 处目的地,随着乘客按顺序输入终点名称的每个字母,候选终点站数目会逐渐减少。
在自动售票机屏幕上,有一个 \(4\) 行 \(8\) 列的键盘,如下图所示。
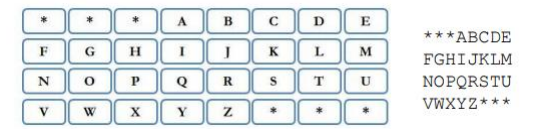
在乘客每输入一个字母后,键盘上只有有效字符是可选的(取决于还有哪些候选终点站),其余的字母会被字符 * 取代。
告诉你 \(N\) 处目的地的名称,以及乘客已经输入的若干字符,请你输出键盘目前的状态。
输入
输入文件名为 kartomat.in。
第一行为一个整数 \(N\)(\(1 \le N \le 50\))。接下来 \(N\) 行,每行一个由大写英文字母组成的长度不超过 \(100\) 的字符串,表示一处目的地。最后一行,一个长度不超过 \(100\) 的字符串,表示按顺序输入的若干字符。
输出
输出文件名为 kartomat.out。
输出 \(4\) 行,每行一个长度为 \(8\) 的字符串,表示键盘状态。
输入示例
4
ZAGREB
SISAK
ZADAR
ZABOK
ZA输出示例
****B*D*
*G******
********
********数据规模及约定
见“输入”
题解
暴力。
// 略数字(rekons)
试题描述
有一天,Mirko 在一张纸上写了 \(N\) 个实数,然后在另一张纸上写下了这些实数的所有整数倍中数值在区间 \([A, B]\) 范围内的所有数(经过去重)。
第二天,Mirko 发现找不到写着 \(N\) 个实数的那张纸了,而只剩下另一张纸。
请你帮助 Mirko 还原原本的 \(N\) 个实数。
注意:本题有 Special Judge。
输入
输入文件名为 rekons.in。
第一行是一个整数 \(K\),表示剩下的那张纸上共有 \(K\) 个实数。
第二行是两个整数 \(A\) 和 \(B\)。
接下来 \(K\) 行,每行一个实数,表示纸上的 \(K\) 个实数。实数已经去重,按递增顺序给出。所有实数至多有 \(5\) 位小数。
输出
输出文件名为 rekons.out。
输出 \(N\) 行,每行一个实数,表示一组解。数据保证有解。如果有多组解,输出 \(N\) 最小的;若还是有多组解,输出任意一组均可。
输入示例1
4
1 2
1
1.4
1.5
2输出示例1
0.5
0.7输入示例2
5
10 25
12
13.5
18
20.25
24输出示例2
6.0
6.75数据规模及约定
\(30\%\) 的测试数据:\(K \le 12\)。
\(50\%\) 的测试数据:输入的 \(K\) 个实数都是整数。
\(100\%\) 的测试数据:\(1 \le K \le 50\),\(1 \le A < B \le 10^6\)。
题解
直接贪心(将所有数字、两两数字之间的差从小到大排序然后从前往后尽量选取)能够得到 \(90\) 分。
然而这样不对。所以怎么办呢?爆搜!
首先将上面贪心策略选出来的数中(令选出来的数为集合 \(S\)),如果 \(\exists a, b \in S, a|b\),那么删掉 \(a\);再加一个最优性剪枝;最后在卡一下时间(如果搜了 \(900000\) 次就退出,直接使用当前最优解),就过了(还可以在搜之前贪心一下得到一个比较优的解,充分利用最优性剪枝)。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <map>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 55
#define maxm 2560
#define LL long long
int n, cd, cu;
LL L, R, A[maxn], dt[maxm], getd[maxm], use[maxm];
map <LL, int> sol;
int ans, Time;
bool now[maxn];
LL Ans[maxn], nAns[maxn];
bool dfs(int cur, int nans) {
if(nans >= ans) return 0;
bool pass = 1;
rep(i, 1, n) pass &= now[i];
if(pass) return ans = nans, memcpy(Ans, nAns, sizeof(nAns)), 0;
if(cur > cu) {
if(++Time > 900000) return 1;
return 0;
}
bool tmp[maxn], has = 0; memcpy(tmp, now, sizeof(now));
rep(j, 1, n) if(A[j] % use[cur] == 0) has |= !now[j], now[j] = 1;
if(has) {
nAns[nans+1] = use[cur];
if(dfs(cur + 1, nans + 1)) return 1;
memcpy(now, tmp, sizeof(now));
}
if(dfs(cur + 1, nans)) return 1;
return 0;
}
int main() {
freopen("rekons.in", "r", stdin);
freopen("rekons.out", "w", stdout);
n = read();
double x; scanf("%lf", &x);
L = (LL)(x * 1e5 + .5);
scanf("%lf", &x);
R = (LL)(x * 1e5 + .5);
rep(i, 1, n) {
scanf("%lf", &x);
A[i] = (LL)(x * 1e5 + .5);
sol[A[i]] = i;
}
rep(i, 1, n){ rep(j, i + 1, n) dt[++cd] = A[j] - A[i]; dt[++cd] = A[i]; }
int cg = 0;
rep(i, 1, cd) {
LL g = dt[i], nw = (L + g - 1) / g * g; bool ok = 1, has = 0;
while(nw <= R) {
if(!sol.count(nw)){ ok = 0; break; }
if(!now[sol[nw]]) has = 1;
nw += g;
}
if(ok) getd[++cg] = g;
if(!ok || !has) continue;
nw = (L + g - 1) / g * g;
while(nw <= R) now[sol[nw]] = 1, nw += g;
Ans[++ans] = g;
}
rep(i, 1, cg) {
bool ok = 1;
rep(j, 1, i - 1) if(getd[i] % getd[j] == 0){ ok = 0; break; }
if(ok) use[++cu] = getd[i];
}
memset(now, 0, sizeof(now));
random_shuffle(use + 1, use + cu + 1);
dfs(1, 0);
rep(i, 1, ans) printf("%.5lf\n", (double)Ans[i] / 1e5);
fclose(stdin);
fclose(stdout);
return 0;
}词韵(rima)
试题描述
Adrian 很喜欢诗歌中的韵。他认为,两个单词押韵当且仅当它们的最长公共后缀的长度至少是其中较长单词的长度减一。也就是说,单词 \(A\) 与单词 \(B\) 押韵当且仅当 \(LCS(A, B) \ge \mathrm{max}(|A|, |B|) – 1\)。(其中 \(LCS\) 是最长公共后缀 longest common suffix 的缩写)
现在,Adrian 得到了 \(N\) 个单词。他想从中选出尽可能多的单词,要求它们能组成一个单词序列,使得单词序列中任何两个相邻单词是押韵的。
输入
输入文件名为 rima.in。
第一行是一个整数 \(N\)。
接下来 \(N\) 行,每行一个由小写英文字母组成的字符串,表示每个单词。所有单词互不相同。
输出
输出文件名为 rima.out。
输出一行,为一个整数,表示最长单词序列的长度。
输入示例
5
ask
psk
k
krafna
sk输出示例
4数据规模及约定
\(30\%\) 的测试数据:\(1 \le N \le 20\),所有单词长度之和不超过 \(3000\)。
\(100\%\) 的测试数据:\(1 \le N \le 500000\),所有单词长度之和不超过 \(3000000\)。
题解
把串反过来建一棵 trie,然后就变成在树上找一条路径,路径中相邻两个点的 lca 与这两个点距离最多为 \(1\),于是就变成树形 dp 了。分两种情况转移:路径一端在根节点和两端都不在根节点。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 3000010
#define x first
#define y second
int ToT, val[maxn], head[maxn], nxt[maxn], ch[maxn];
void Insert(char *S) {
int u = 1, n = strlen(S);
dwn(i, n - 1, 0) {
int c = S[i] - '0';
bool has = 0;
for(int e = head[u]; e; e = nxt[e]) if(ch[e] == c){ has = 1; u = e; break; }
if(!has) {
nxt[++ToT] = head[u]; ch[ToT] = c; head[u] = ToT;
u = ToT;
}
}
val[u]++;
return ;
}
int f[2][maxn];
void dp(int u) {
int cnts = 0, mx = -1, mx2 = -1;
for(int e = head[u]; e; e = nxt[e]) {
dp(e); cnts += val[e];
int nval = f[1][e] - val[e];
if(nval > mx) mx2 = mx, mx = nval;
else if(nval > mx2) mx2 = nval;
}
cnts += val[u];
if(val[u]) f[1][u] = cnts + max(mx, 0);
if(mx2 >= 0) f[0][u] = cnts + mx + mx2;
// printf("f[%d]: %d %d\n", u, f[0][u], f[1][u]);
return ;
}
int n;
char S[maxn];
int main() {
freopen("rima.in", "r", stdin);
freopen("rima.out", "w", stdout);
ToT = 1;
n = read();
rep(i, 1, n) scanf("%s", S), Insert(S);
dp(1);
int ans = 0;
rep(i, 1, ToT) ans = max(ans, max(f[0][i], f[1][i]));
printf("%d\n", ans);
fclose(stdin);
fclose(stdout);
return 0;
}八维(osm)
试题描述
我们将一个 \(M\) 行 \(N\) 列的字符矩阵无限复制,可以得到一个无限字符矩阵。
例如,对于以下矩阵
 ,
,
可以无限复制出矩阵
 。
。
我们认为矩阵是八连通的。八连通,指矩阵中的每个位置与上下左右和四个斜向(左上、右上、左下、右下)的位置相邻。因此,从矩阵任意位置出发沿八个方向中的任意一个都可以无限延长。
如果我们随机选择一个位置和一个方向,则可以从此位置开始沿此方向连续选取 \(K\) 个字符组成一个字符串。问,两次这样操作得到两个相同字符串的概率是多少。(假设随机选择时任意位置是等可能的,任意方向也是等可能的)
输入
输入文件名为 osm.in。
第一行是三个整数 \(M\),\(N\),\(K\)。
接下来 \(M\) 行,每行一个由小写英文字母组成的长度为 \(N\) 的字符串,即 \(M \times N\) 的字符矩阵。保证矩阵中至少出现两种不同字符。
输出
输出文件名为 osm.out。
输出一行,为一个化简后的分数,表示概率。
输入示例1
1 2 2
ab输出示例1
5/16输入示例2
3 3 10
ban
ana
nab输出示例2
2/27数据规模及约定
\(30\%\) 的测试数据:\(M, N \le 10\),\(K \le 100\)。
\(50\%\) 的测试数据:\(M = N\)。
\(100\%\) 的测试数据:\(1 \le M, N \le 500\),\(2 \le K \le 10^9\)。
题解
由于这个无限矩阵是无限复制得到的,所以算概率只需要关注以里面的 \(M \times N\) 个格子作为起点的,八个方向的 \(8MN\) 个串就可以了,然后相同的串记一个数,最后求的就是每个本质不同的串的数目的平方和。
我们可以倍增维护一个长度为 \(K\) 的串。具体来讲,先枚举一个方向 \(d\),我们维护 \(H(k, i, j)\) 表示以 \((i, j)\) 为起点,向方向 \(d\) 延伸 \(2^k\) 长度的串的 hash 值。具体怎么转移维护请读者思考。
开 unsigned long long 才能过,unsigned int 会有冲突。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 500
#define maxnode 1000010
#define maxlog 30
#define UI unsigned long long
#define rate 233
#define LL long long
int n, m, K;
UI key[maxlog][maxn][maxn], rpow[maxlog];
char Map[maxn][maxn];
const int HMOD = 1000037, dirx[8] = {-1, -1, -1, 0, 0, 1, 1, 1}, diry[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
struct Hash {
int ToT, head[HMOD], nxt[maxnode], val[maxnode];
UI key[maxnode];
int Find(UI x) {
int u = x % HMOD;
for(int e = head[u]; e; e = nxt[e]) if(key[e] == x) return e;
return 0;
}
void Insert(UI x) {
int tmp = Find(x);
if(tmp) return (void)(val[tmp]++);
int u = x % HMOD;
nxt[++ToT] = head[u]; val[ToT] = 1; key[ToT] = x; head[u] = ToT;
return ;
}
} hh;
LL gcd(LL a, LL b){ return b ? gcd(b, a % b) : a; }
int main() {
freopen("osm.in", "r", stdin);
freopen("osm.out", "w", stdout);
n = read(); m = read(); K = read();
rep(i, 0, n - 1) scanf("%s", Map[i]);
rep(d, 0, 7) {
rep(i, 0, n - 1) rep(j, 0, m - 1) key[0][i][j] = Map[i][j] - 'a';
rpow[0] = rate;
for(int s = 1; (1 << s) <= K; s++) {
rpow[s] = rpow[s-1] * rpow[s-1];
rep(i, 0, n - 1) rep(j, 0, m - 1) {
int x = (i + dirx[d] * (1 << s >> 1) % n + n) % n, y = (j + diry[d] * (1 << s >> 1) % m + m) % m;
key[s][i][j] = key[s-1][i][j] * rpow[s-1] + key[s-1][x][y];
}
}
rep(i, 0, n - 1) rep(j, 0, m - 1) {
int k = K, x = i, y = j; UI now = 0;
dwn(s, maxlog - 1, 0) if(k >= (1 << s)) {
now = now * rpow[s] + key[s][x][y];
k -= 1 << s;
x = (x + dirx[d] * (1 << s) % n + n) % n;
y = (y + diry[d] * (1 << s) % m + m) % m;
}
hh.Insert(now);
}
}
LL A = 0, B = (LL)n * m * 8 * n * m * 8;
rep(i, 1, hh.ToT) A += (LL)hh.val[i] * hh.val[i];
LL g = gcd(A, B); A /= g; B /= g;
printf("%lld/%lld\n", A, B);
fclose(stdin);
fclose(stdout);
return 0;
}day2
魔法串(magic)
试题描述
小 N 最近在沉迷数学问题。
对于一个数字串 \(S\),如果可以将它划分成两个数字 \(A\)、\(B\),满足:
1、\(\overline{S} = \overline{AB}\)。
2、\(A\)、\(B\) 均不包含前导 \(0\)。
3、\(B\) 是 \(A\) 的倍数,且是完全立方数。
那么小 N 就认为该划分是一个“好划分”。如对于数字串 \(11297\),\((11, 297)\) 就是一个“好划分”。
如果一个数字串 \(S\) 至少有两个“好划分”,那么小 N 就认为 \(S\) 是一个“魔法串”。如数字串 \(1335702375\) 就是一个“魔法串”,其“好划分”有 \((1,335702375)\) 和 \((133,5702375)\)。
现在给定正整数 \(N\),小 N 需要你帮她求出一个长度恰好为 \(N\) 的“魔法串”\(S\),如果无解请输出 QwQ。
输入
一行一个正整数 \(N\)。
输出
一行一个长度恰好为 \(N\) 的“魔法串”\(S\),如果无解请输出 QwQ。
输入示例
19输出示例
1124784124392112128数据规模及约定
对于 \(30\%\) 的数据:\(1 \le N \le 10\)。
对于 \(50\%\) 的数据:\(1 \le N \le 35\)。
对于 \(100\%\) 的数据:\(1 \le N \le 100\)。
题解
对于一个魔法串 \(S\),有 \(\overline{S000}\) 是魔法串。所以我们只需要将 \(N\) 模 \(3\) 分类,找到每一类中最短的那个就好了。
通过搜索发现当 \(N < 5\) 时无解,\(N = 5, 6, 7\) 时搜出来就好了。
搜索程序(输入 \(N\),它会搜出长度为 \(N\) 的一个魔法串,我们只需要分别输入 \(5, 6, 7\) 就好了):
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i++)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 10
#define LL long long
int n, A[maxn];
bool check() {
int x = 0, y, cnt = 0;
rep(i, 1, n) {
x = x * 10 + A[i];
if(!A[i+1]) continue;
y = 0;
rep(j, i + 1, n) y = y * 10 + A[j];
if(y % x == 0) {
int t = (int)pow(y / x, 1.0 / 3.0);
if(((LL)t * t * t == y / x || (LL)(t + 1) * (t + 1) * (t + 1) == y / x || (LL)(t - 1) * (t - 1) * (t - 1) == y / x)) {
// printf("here: %d %d\n", x, y);
if(++cnt == 2) return 1;
}
}
}
return 0;
}
void dfs(int cur) {
if(cur > n) {
if(check()){ rep(i, 1, n) printf("%d", A[i]); putchar('\n'); exit(0); }
return ;
}
for(A[cur] = cur == 1 ? 1 : 0; A[cur] <= 9; A[cur]++) dfs(cur + 1);
return ;
}
int main() {
n = read();
dfs(1);
return 0;
}最终程序:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
int num[3] = {324000, 1621296, 73584}, bit[3] = {6, 7, 5};
int main() {
freopen("magic.in", "r", stdin);
freopen("magic.out", "w", stdout);
int n = read();
if(n < 5) return puts("QwQ"), 0;
printf("%d", num[n%3]); rep(i, 1, (n - bit[n%3]) / 3) printf("000"); putchar('\n');
fclose(stdin);
fclose(stdout);
return 0;
}数字统计(count)
试题描述
小 A 正在研究一些数字统计问题。有一天他突然看到了一个这样的问题:
将 \([L..R]\) 中的所有整数用 \(M\) 位二进制数表示(允许出现前导 \(0\))。现在将这些数中的每一个作如下变换:
从这个数的最低两位开始,如果这两位都是 \(0\),那么 \(X=1\),否则 \(X=0\)。现在将这两位删去,然后将 \(X\) 放在原来最低位的位置上。重复这个变换直到这个数只剩下一位为止。
例如 \(01001\) 的变换过程如下:
\(01001 \rightarrow 0100 \rightarrow 011 \rightarrow 00 \rightarrow 1\)。
现在的问题是变换后的所有数中,值为 \(Y\)(\(Y\) 为 \(0\) 或 \(1\))的有多少个?
小 A 不会了,他想让你帮助他完成这个问题。
输入
输入文件包含多组测试数据。
第一行,一个整数 \(T\),表示测试数据的组数。
接下来的 \(T\) 节,每节对应一组测试数据,格式如下:
第一行,两个整数 \(M\)、\(Y\)。
第二行,两个 \(M\) 位二进制数 \(L\)、\(R\)。
输出
对于每组测试数据,输出一行,一个二进制数,表示该组测试数据中 \([L..R]\) 中的所有整数变换后的值为 \(Y\) 的个数。这里的二进制数不允许出现前导 \(0\)。
输入示例
1
3 1
001 101输出示例
11数据规模及约定
对于 \(20\%\) 的数据:\(1 \le M \le 16\)。
对于 \(40\%\) 的数据:\(1 \le M \le 32\)。
对于 \(100\%\) 的数据:\(1 \le M \le 200\),\(1 \le T \le 50\)。
题解
由于只要两位中有一个 \(1\) 都会变成 \(0\),所以关键就要看最靠左的 \(1\) 位置。
若最左的 \(1\) 的位置在奇数位(位置从 \(1\) 开始标号),那么最终会变成 \(0\),否则最终变成 \(1\)。注意特判最后一位,最后一位是 \(1\) 等价于倒数第二位是 \(1\)。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 210
int n, L[maxn], R[maxn], tmp[maxn], tt[maxn], ans[maxn];
char Lc[maxn], Rc[maxn];
void Plus(int *a, int *b) {
rep(i, 1, n) a[i] += b[i];
dwn(i, n, 1) a[i-1] += a[i] >> 1, a[i] &= 1;
return ;
}
void Minus(int *ans, int *a, int *b) {
rep(i, 1, n) ans[i] = a[i] - b[i];
dwn(i, n, 1) {
if(ans[i] < 0) ans[i-1] -= 1 - ans[i] >> 1;
ans[i] = abs(ans[i]) & 1;
}
return ;
}
void work() {
n = read(); int Y = read();
scanf("%s%s", Lc + 1, Rc + 1);
int st = 1, lst = 1; while(st <= n && Rc[st] == '0') st++;
rep(i, 1, n) L[i] = Lc[i] - '0', R[i] = Rc[i] - '0';
while(lst <= n && !L[lst]) lst++;
memset(ans, 0, sizeof(ans));
if(!Y) {
if(R[st] == L[st] && !(st & 1)) return (void)puts("0");
if(R[st] == L[st]) {
Minus(ans, R, L);
memset(tt, 0, sizeof(tt));
tt[n] = 1;
Plus(ans, tt);
}
else {
for(int i = 1; i <= lst; i += 2) if(st <= i) {
if(i == n && !(n - 1 & 1)) break;
if(i == st) {
R[st] = 0;
// printf("1+ "); rep(j, 1, n) printf("%d", R[j]); putchar('\n');
R[st] = 0; Plus(ans, R); R[st] = 1;
memset(tt, 0, sizeof(tt)); tt[n] = 1;
Plus(ans, tt);
}
else if(i == lst) {
memset(tt, 0, sizeof(tt));
tt[i] = 1;
L[i] = 0;
Minus(tmp, tt, L);
L[i] = 1;
// printf("2+ "); rep(j, 1, n) printf("%d", tmp[j]); putchar('\n');
Plus(ans, tmp);
}
else {
memset(tt, 0, sizeof(tt));
tt[i] = 1;
// printf("3+ "); rep(j, 1, n) printf("%d", tt[j]); putchar('\n');
Plus(ans, tt);
}
if(n - i <= 2 && i < n) i = n - 2;
}
}
}
else {
if(R[st] == L[st] && (st & 1)) return (void)puts("0");
if(R[st] == L[st]) {
Minus(ans, R, L);
memset(tt, 0, sizeof(tt));
tt[n] = 1;
Plus(ans, tt);
}
else {
for(int i = 2; i <= lst; i += 2) if(st <= i) {
if(i == n && (n - 1 & 1)) break;
if(i == st) {
R[st] = 0;
// printf("1+ "); rep(j, 1, n) printf("%d", R[j]); putchar('\n');
R[st] = 0; Plus(ans, R); R[st] = 1;
memset(tt, 0, sizeof(tt)); tt[n] = 1;
Plus(ans, tt);
}
else if(i == lst) {
memset(tt, 0, sizeof(tt));
tt[i] = 1;
L[i] = 0;
Minus(tmp, tt, L);
L[i] = 1;
// printf("2+ "); rep(j, 1, n) printf("%d", tmp[j]); putchar('\n');
Plus(ans, tmp);
}
else {
memset(tt, 0, sizeof(tt));
tt[i] = 1;
// printf("3+ "); rep(j, 1, n) printf("%d", tt[j]); putchar('\n');
Plus(ans, tt);
}
if(n - i <= 2 && i < n) i = n - 2;
}
}
}
st = 1;
while(st <= n && !ans[st]) st++;
if(st > n) puts("0");
else { for(; st <= n; st++) printf("%d", ans[st]); putchar('\n'); }
return ;
}
int main() {
freopen("count.in", "r", stdin);
freopen("count.out", "w", stdout);
int T = read();
while(T--) work();
fclose(stdin);
fclose(stdout);
return 0;
}基础匹配算法练习题(match)
试题描述
小 S 最近学会了二分图匈牙利匹配算法。
现在二分图的 \(X\) 部有 \(N\) 个数字 \(A_i\),\(Y\) 部有 \(K\) 个数字 \(C_i\)。
已知如果 \(A_i + C_j \le Z\),那么 \(A_i\) 和 \(C_j\) 之间就有一条边,求二分图 \((X, E, Y)\) 的最大匹配数。
小 S 是初学者,所以她想做多做一些练习来巩固知识。于是她找到了一个长度为 \(M\) 的正整数数组 \(B[]\),每次她会在 \(B[]\) 数组中抽取一段连续的区间 \([L_i,R_i]\),把区间 \([L_i,R_i]\) 的所有数字作为二分图 \(Y\) 部的 \(K\) 个数字 \(C_i\),然后重新求一次二分图最大匹配数。
小 S 打算一共做 \(Q\) 次练习,但是她不知道每次计算出的答案对不对,你能帮帮她吗?
输入
第一行为三个正整数 \(N\)、\(M\)、\(Z\)。
第二行为 \(N\) 个正整数,第 \(i\) 个正整数表示 \(A_i\)。
第三行为 \(M\) 个正整数,第 \(i\) 个正整数表示 \(B_i\)。
接下来 \(Q\) 行每行两个正整数,第 \(i\) 行的两个正整数分别表示 \(L_i\)、\(R_i\)。
输出
对于每次练习,输出该次练习的答案。
输入示例
4 10 8
1 2 4 6
6 3 6 2 8 4 9 10 6 8
4
1 4
2 5
5 6
1 6输出示例
4
3
1
4数据规模及约定
| 测试数据编号 | $N$ | $M$ | $Q$ |
|---|---|---|---|
| 1 - 4 | $\le 50$ | $\le 50$ | $\le 50$ |
| 5 - 10 | $\le 2501$ | $\le 2501$ | $\le 2501$ |
| 11 - 14 | $\le 152501$ | $\le 45678$ | $\le 45678$ |
| 15 - 16 | $\le 152501$ | $\le 50$ | $\le 52501$ |
| 17 - 20 | $\le 152501$ | $\le 52501$ | $\le 52501$ |
对于 \(100\%\) 的数据:\(1 \le A_i, B_i, Z \le 10^9\),\(1 \le L_i \le R_i \le Q\)。
保证数据有一定梯度。
题解
这是一个假的二分图匹配,可以贪心搞。
考虑将 \(A\) 从小到大排序,然后对于 \(B_i\) 求出 \(f_i\) 使得 \(A_{f_i} + B_i \le Z\) 且 \(f_i\) 最大。那么对于一个区间内的 \(f_i\),我们在 \(A\) 数组对应位置上打上标记,然后从右往左扫,每往左一格就减一,遇到一个标记就加上这个标记,然后最后剩下的数字就是 \(B\) 中没有匹配上的。
那么 \(R_q - L_q + 1 - \max \{ S_i - i \}\) 就是答案了,其中 \(S_i\) 表示位置 \(i\) 的标记的前缀和。
这样的话莫队 + 线段树暴力做。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 152510
#define maxm 52510
int n, m, Z, A[maxn], B[maxm], num[maxm], bl[maxm], Ans[maxm];
struct Que {
int l, r, id;
Que() {}
Que(int _1, int _2, int _3): l(_1), r(_2), id(_3) {}
bool operator < (const Que& t) const {
if(bl[l] != bl[t.l]) return bl[l] < bl[t.l];
if(bl[l] & 1) return r < t.r;
else return r > t.r;
}
} qs[maxm];
int mxv[maxn<<2], addv[maxn<<2];
void build(int o, int l, int r) {
if(l == r) mxv[o] = -num[l];
else {
int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
build(lc, l, mid); build(rc, mid + 1, r);
mxv[o] = max(mxv[lc], mxv[rc]);
}
return ;
}
void pushdown(int o, int l, int r) {
if(!addv[o] || l == r) return (void)(addv[o] = 0);
int lc = o << 1, rc = lc | 1;
addv[lc] += addv[o]; mxv[lc] += addv[o];
addv[rc] += addv[o]; mxv[rc] += addv[o];
addv[o] = 0;
return ;
}
void update(int o, int l, int r, int ql, int v) {
pushdown(o, l, r);
if(ql <= l) addv[o] += v, mxv[o] += v;
else {
int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
if(ql <= mid) update(lc, l, mid, ql, v);
update(rc, mid + 1, r, ql, v);
mxv[o] = max(mxv[lc], mxv[rc]);
}
return ;
}
int main() {
freopen("match.in", "r", stdin);
freopen("match.out", "w", stdout);
n = read(); m = read(); Z = read();
rep(i, 1, n) A[i] = read(); sort(A + 1, A + n + 1);
int bsiz = (int)sqrt((double)m);
rep(i, 1, m) {
int v = read();
num[i] = B[i] = upper_bound(A + 1, A + n + 1, Z - v) - A - 1;
bl[i] = (i - 1) / bsiz + 1;
}
sort(num + 1, num + m + 1);
int cm = unique(num + 1, num + m + 1) - num - 1;
rep(i, 1, m) B[i] = lower_bound(num + 1, num + cm + 1, B[i]) - num;
int q = read();
rep(i, 1, q) {
int l = read(), r = read();
qs[i] = Que(l, r, i);
}
sort(qs + 1, qs + q + 1);
build(1, 0, cm);
int nl = 1, nr = 1; update(1, 0, cm, B[1], 1);
rep(i, 1, q) {
int ql = qs[i].l, qr = qs[i].r;
while(nl < ql) update(1, 0, cm, B[nl], -1), nl++;
while(nl > ql) update(1, 0, cm, B[nl-1], 1), nl--;
while(nr < qr) update(1, 0, cm, B[nr+1], 1), nr++;
while(nr > qr) update(1, 0, cm, B[nr], -1), nr--;
Ans[qs[i].id] = qr - ql + 1 - mxv[1];
}
rep(i, 1, q) printf("%d\n", Ans[i]);
fclose(stdin);
fclose(stdout);
return 0;
}上学路线(path)
试题描述
小 B 所在的城市的道路构成了一个方形网格,它的西南角为 \((0,0)\),东北角为 \((N,M)\)。
小 B 家住在西南角,学校在东北角。现在有 \(T\) 个路口进行施工,小 B 不能通过这些路口。小 B 喜欢走最短的路径到达目的地,因此他每天上学时都只会向东或北行走;而小 B 又喜欢走不同的路径,因此他问你按照他走最短路径的规则,他可以选择的不同的上学路线有多少条。由于答案可能很大,所以小 B 只需要让你求出路径数 \(\mod P\) 的值。
输入
第一行为四个整数 \(N\)、\(M\)、\(T\)、\(P\)。
接下来的 \(T\) 行,每行两个整数,表示施工的路口的坐标。
输出
一行一个整数,表示路径数 \(\mod P\) 的值。
输入示例
3 4 3 1019663265
3 0
1 1
2 2输出示例
8数据规模及约定
| 测试点编号 | $N$、$M$ 的范围 | $T$ 的范围 | $P$ 的范围 |
|---|---|---|---|
| 1 - 2 | $1 \le N, M \le 1000$ | $0 \le T \le 200$ | $P = 1019663265$ |
| 3 - 4 | $1 \le N, M \le 100000$ | $T = 0$ | $P = 1000003$ |
| 5 - 6 | $1 \le N, M \le 10^9$ | $P = 1019663265$ | |
| 7 - 8 | $1 \le N, M \le 100000$ | $0 \le T \le 200$ | $P = 1000003$ |
| 9 - 10 | $1 \le N, M \le 10^9$ | $P = 1019663265$ |
对于 \(100\%\) 的数据:\(1 \le A_i, B_i, Z \le 10^9\),\(1 \le L_i \le R_i \le Q\)。
保证数据有一定梯度。
题解
考虑容斥原理,令 \(f(i)\) 表示从起点走到 \(i\) 并且不经过 \(i\) 左下角任何点的方案数。我们可以先暴力从起点走到 \(i\),不考虑限制,然后减掉“第一次”出现错误的地方分别在每个点的方案数,形式化地:
\[ f(i) = C_{x_i + y_i}^{x_i} - \sum_{j=1}^n [j 在 i 左下] f(j) C_{x_i - x_j + y_i - y_j} ^ {x_i - x_j} \]
对于 \(P = 1000003\) 的数据直接做,预处理一下阶乘和阶乘逆元;由于 \(1019663265 = 3 \times 5 \times 6793 \times 10007\),那么用 lucas 定理,然后中国剩余定理合并即可。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
#define LL long long
LL read() {
LL x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 200010
#define maxg 1010
#define maxt 210
LL n, m;
int ct, MOD;
#define pll pair <LL, LL>
#define x first
#define y second
#define mp(x, y) make_pair(x, y)
pll ps[maxt];
int fac[maxn], ifac[maxn], F[maxt][maxt], Ans[maxt];
LL C(int n, int m) {
return (LL)fac[n] * ifac[m] % MOD * ifac[n-m] % MOD;
}
void solve1() {
rep(i, 1, ct) {
int X = read(), Y = read();
ps[i] = mp(X, Y);
}
fac[0] = ifac[0] = 1;
ifac[1] = 1;
rep(i, 2, n + m) ifac[i] = (LL)(MOD - MOD / i) * ifac[MOD%i] % MOD;
rep(i, 1, n + m) ifac[i] = (LL)ifac[i] * ifac[i-1] % MOD, fac[i] = (LL)fac[i-1] * i % MOD;
ps[++ct] = mp(n, m);
sort(ps + 1, ps + ct + 1);
rep(t, 1, ct) {
Ans[t] = C(ps[t].x + ps[t].y, ps[t].x);
rep(mid, 1, t - 1) if(ps[mid].x <= ps[t].x && ps[mid].y <= ps[t].y) {
int tmp = C((ps[t].x - ps[mid].x) + (ps[t].y - ps[mid].y), ps[t].x - ps[mid].x);
tmp = (LL)tmp * Ans[mid] % MOD;
Ans[t] = (Ans[t] - tmp + MOD) % MOD;
}
}
printf("%d\n", Ans[ct]);
return ;
}
void gcd(LL a, LL b, LL& x, LL& y) {
if(!b){ x = 1; y = 0; return ; }
gcd(b, a % b, y, x); y -= a / b * x;
return ;
}
const int need = 10017;
int Fac[4][need], iFac[4][need], prime[4] = {3, 5, 6793, 10007};
LL Cm(int n, int m, int Mid) {
return (LL)Fac[Mid][n] * iFac[Mid][m] % prime[Mid] * iFac[Mid][n-m] % prime[Mid];
}
LL calc(LL n, LL m, int Mid) {
if(n < m) return 0;
if(n < prime[Mid] && m < prime[Mid]) return Cm(n, m, Mid);
return (LL)calc(n / prime[Mid], m / prime[Mid], Mid) * calc(n % prime[Mid], m % prime[Mid], Mid) % prime[Mid];
}
int Ch(LL n, LL m) {
int a1 = calc(n, m, 0), a2 = calc(n, m, 1), a3 = calc(n, m, 2), a4 = calc(n, m, 3);
LL x, y; gcd(3ll, 5ll, x, y); x *= a1 - a2; x = (x % 15 + 15) % 15; a1 = ((a1 - x * 3) % 15 + 15) % 15; a2 = a3;
gcd(15ll, 6793ll, x, y); x *= a1 - a2; x = (x % 101895 + 101895) % 101895; a1 = ((a1 - x * 15) % 101895 + 101895) % 101895; a2 = a4;
gcd(101895ll, 10007ll, x, y); x *= a1 - a2; x = (x % MOD + MOD) % MOD; a1 = ((a1 - x * 101895) % MOD + MOD) % MOD;
return a1;
}
void solve2() {
rep(i, 1, ct) {
int X = read(), Y = read();
ps[i] = mp(X, Y);
}
rep(pr, 0, 3) {
Fac[pr][0] = iFac[pr][0] = 1;
iFac[pr][1] = 1;
rep(i, 2, prime[pr] - 1) iFac[pr][i] = (LL)(prime[pr] - prime[pr] / i) * iFac[pr][prime[pr]%i] % prime[pr];
rep(i, 1, prime[pr] - 1) iFac[pr][i] = (LL)iFac[pr][i] * iFac[pr][i-1] % MOD, Fac[pr][i] = (LL)Fac[pr][i-1] * i % MOD;
}
ps[++ct] = mp(n, m);
sort(ps + 1, ps + ct + 1);
rep(t, 1, ct) {
Ans[t] = Ch(ps[t].x + ps[t].y, ps[t].x);
rep(mid, 1, t - 1) if(ps[mid].x <= ps[t].x && ps[mid].y <= ps[t].y) {
int tmp = Ch((ps[t].x - ps[mid].x) + (ps[t].y - ps[mid].y), ps[t].x - ps[mid].x);
tmp = (LL)tmp * Ans[mid] % MOD;
Ans[t] = (Ans[t] - tmp + MOD) % MOD;
}
}
printf("%d\n", Ans[ct]);
return ;
}
int main() {
freopen("path.in", "r", stdin);
freopen("path.out", "w", stdout);
n = read(); m = read(); ct = read(); MOD = read();
if(MOD == 1000003) solve1();
else solve2(); // MOD = 3 * 5 * 6793 * 10007
fclose(stdin);
fclose(stdout);
return 0;
}day3
第 k 大斜率(slope)
试题描述
在平面直角坐标系上,有 \(n\) 个不同的点。任意两个不同的点确定了一条直线。请求出所有斜率存在的直线按斜率从大到小排序后,第 \(k\) 条直线的斜率为多少。
为了避免精度误差,请输出斜率向下取整后的结果。(例如:\(\lfloor 1.5 \rfloor = 1\) ,\(\lfloor −1.5 \rfloor = −2\))
输入
第一行,包含两个正整数 \(n\) 和 \(k\) 。
接下来 \(n\) 行,每行包含两个整数 \(x_i, y_i\),表示每个点的横纵坐标。
输出
输出一行,包含一个整数,表示第 \(k\) 小的斜率向下取整的结果。
输入示例
4 1
-1 -1
2 1
3 3
1 4输出示例
2数据规模及约定
令 $M = 所有斜率存在且大于 0 的直线的数量 $。
对于 \(10\%\) 的数据,\(1 \le n \le 10\)。
对于 \(20\%\) 的数据,\(1 \le n \le 100\) ,\(|x_i|, |y_i| \le 10^3\)。
对于 \(30\%\) 的数据,\(1 \le n \le 1000\)。
对于 \(40\%\) 的数据,\(1 \le n \le 5000\)。
对于另 \(20\%\) 的数据,满足 \(k = 1\)。
对于另 \(20\%\) 的数据,满足 \(1 \le x_i, y_i \le 10^3\) 。
对于 \(100\%\) 的数据,\(1 \le n \le 100000\),\(k \le M\) ,\(|x_i|, |y_i| \le 10^8\)。
题解
二分答案 \(k\),问题转化成了求斜率 \(\ge k\) 的直线有多少条。
如果一个过 \((x_0, y_0), (x_1, y_1)\) 的直线满足斜率 \(\ge k\),那么就是要满足
\[ \frac{y_1 - y_0}{x_1 - x_0} \ge k \]
如果我们令 \(x_1 > x_0\),那么可以移项得到
\[ y_1 - y_0 \ge kx_1 - kx_0 \\\\ y_1 - kx_1 \ge y_0 - kx_0 \]
于是我们将所有点按照横坐标从大到小排序(若横坐标相等则要纵坐标从小到大,这样能够避免对无穷大斜率的直线的统计),然后按顺序查询点 \(i\) 和后面的哪些点 \(j(j > i)\) 能够满足 \(y_i - kx_i \le y_j - kx_j\),将这样的 \(j\) 的个数累加,插入点 \(i\),就可以完成斜率 \(\ge k\) 的直线的数目统计了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
#define LL long long
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
LL read() {
LL x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = Getchar(); }
return x * f;
}
#define maxn 100010
struct Point {
int x, y;
Point() {}
Point(int _, int __): x(_), y(__) {}
bool operator < (const Point& t) const { return x != t.x ? x < t.x : y > t.y; }
} ps[maxn];
int n;
LL K;
int sumv[maxn<<2];
void update(int o, int l, int r, int p) {
if(l == r) sumv[o]++;
else {
int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
if(p <= mid) update(lc, l, mid, p);
else update(rc, mid + 1, r, p);
sumv[o] = sumv[lc] + sumv[rc];
}
return ;
}
int query(int o, int l, int r, int ql) {
if(ql <= l) return sumv[o];
int mid = l + r >> 1, lc = o << 1, rc = lc | 1, ans = query(rc, mid + 1, r, ql);
if(ql <= mid) ans += query(lc, l, mid, ql);
return ans;
}
LL val[maxn], num[maxn];
LL total(int k) {
rep(i, 1, n) num[i] = val[i] = (LL)ps[i].y - (LL)k * ps[i].x;
sort(num + 1, num + n + 1);
rep(i, 1, n) val[i] = lower_bound(num + 1, num + n + 1, val[i]) - num;
memset(sumv, 0, sizeof(sumv));
LL ans = 0;
dwn(i, n, 1) {
ans += query(1, 1, n, val[i]);
update(1, 1, n, val[i]);
}
// printf("total(%d) = %lld\n", k, ans);
return ans;
}
int main() {
freopen("slope.in", "r", stdin);
freopen("slope.out", "w", stdout);
n = read(); K = read();
rep(i, 1, n) {
int x = read(), y = read();
ps[i] = Point(x, y);
}
sort(ps + 1, ps + n + 1);
int l = -(int)2e8, r = (int)2e8 + 1;
while(r - l > 1) {
int mid = l + r >> 1;
if(total(mid) < K) r = mid; else l = mid;
}
printf("%d\n", l);
fclose(stdin);
fclose(stdout);
return 0;
}餐巾计划问题(napkin)
试题描述
一个餐厅在相继的 \(n\) 天里,每天需用的餐巾数不尽相同。假设第 \(i\) 天(\(i = 1,2, \cdots , n\)) 需要 \(r_i\) 块餐巾。餐厅可以在任意时刻购买新的餐巾,每块餐巾的费用为 \(p\) 。使用过的旧餐巾,则需要经过清洗才能重新使用。把一块旧餐巾送到清洗店 A,需要等待 \(m_1\) 天后才能拿到新餐巾,其费用为 \(c_1\) ;把一块旧餐巾送到清洗店 B,需要等待 \(m_2\) 天后才能拿到新餐巾,其费用为 \(c_2\) 。例如,将一块第 \(k\) 天使用过的餐巾送到清洗店 A 清洗,则可以在第 \(k + m_1\) 天使用。
请为餐厅合理地安排好 \(n\) 天中餐巾使用计划,使总的花费最小。
输入
第一行,包含六个个正整数 \(n, m_1, m_2, c_1, c_2, p\)。
接下来输入 \(n\) 行,每行包含一个正整数 \(r_i\) 。
输出
输出一行,包含一个正整数,表示最小的总花费。
输入示例
4 1 2 2 1 3
8
2
1
6输出示例
35数据规模及约定
对于 \(30\%\) 的数据,\(1 \le n \le 5\) ,\(1 \le c_1, c_2, p \le 5\) ,\(1 \le r_i \le 5\)。
对于 \(50\%\) 的数据,\(1 \le n \le 100\),\(1 \le r_i \le 50\)。
对于 \(70\%\) 的数据,\(1 \le n \le 5000\)。
对于 \(100\%\) 的数据,\(1 \le n \le 200000\),\(1 \le m_1, m_2 \le n\) ,\(1 \le c_1, c_2, p \le 100\),\(1 \le r_i \le 100\)。
题解
这题写费用流就输了……
我们假设已经知道了使用的餐巾数量 \(x\),那么这 \(n\) 天的使用情况就可以贪心了。首先优先使用新买的餐巾,然后优先使用慢洗能来得及的餐巾,接着优先使用日期靠后的快洗来得及的餐巾。
考虑费用流暴力增广的过程,在满足最大流(即满足购买的餐巾数量足够)的情况下,每次增加 \(1\) 的流量(即多买 \(1\) 块餐巾),最短路都会变长。开始时最短路是负数,到一定时候最短路会变正,所以我们发现最后费用关于餐巾数量 \(x\) 的函数 \(f(x)\) 是一个下凸函数。
于是我们就可以在餐巾足够的范围三分 \(x\) 啦。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <queue>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 200010
#define oo 2147483647
#define pii pair <int, int>
#define x first
#define y second
#define mp(x, y) make_pair(x, y)
int n, m1, m2, c1, c2, p, need[maxn], Need[maxn], sum;
deque <pii > Fast, Slow, Not;
void PushBack(deque <pii >& Q, pii x) {
if(!Q.empty() && Q.back().y == x.y) {
pii t = Q.back(); Q.pop_back();
t.x += x.x; Q.push_back(t);
}
else Q.push_back(x);
return ;
}
void PushFront(deque <pii >& Q, pii x) {
if(!Q.empty() && Q.front().y == x.y) {
pii t = Q.front(); Q.pop_front();
t.x += x.x; Q.push_front(t);
}
else Q.push_front(x);
return ;
}
int calc(int x) {
rep(i, 1, n) need[i] = Need[i];
while(!Fast.empty()) Fast.pop_back();
while(!Slow.empty()) Slow.pop_back();
while(!Not.empty()) Not.pop_back();
int ans = p * x;
rep(i, 1, n) {
while(!Not.empty() && i - Not.front().y >= m1) PushBack(Fast, Not.front()), Not.pop_front();
while(m2 < oo && !Fast.empty() && i - Fast.front().y >= m2) PushBack(Slow, Fast.front()), Fast.pop_front();
if(x >= need[i]) PushBack(Not, mp(need[i], i)), x -= need[i];
else {
if(x) PushBack(Not, mp(x, i)), need[i] -= x, x = 0;
if(m2 < oo) {
while(need[i] > 0 && !Slow.empty()) {
pii now = Slow.front(); Slow.pop_front();
if(now.x >= need[i]) PushBack(Not, mp(need[i], i)), now.x -= need[i], ans += need[i] * c2, need[i] = 0, PushFront(Slow, now);
else PushBack(Not, mp(now.x, i)), need[i] -= now.x, ans += now.x * c2;
}
}
while(need[i] > 0 && !Fast.empty()) {
pii now = Fast.back(); Fast.pop_back();
if(now.x >= need[i]) PushBack(Not, mp(need[i], i)), now.x -= need[i], ans += need[i] * c1, need[i] = 0, PushBack(Fast, now);
else PushBack(Not, mp(now.x, i)), need[i] -= now.x, ans += now.x * c1;
}
if(need[i] > 0) return oo;
}
}
return ans;
}
int main() {
freopen("napkin.in", "r", stdin);
freopen("napkin.out", "w", stdout);
n = read(); m1 = read(); m2 = read(); c1 = read(); c2 = read(); p = read();
rep(i, 1, n) Need[i] = need[i] = read(), sum += need[i];
// 1: faster; 2: slower.
if(m1 > m2) swap(m1, m2), swap(c1, c2);
if(c1 < c2) m2 = c2 = oo;
int l = 1, r = sum;
while(l < r) {
int mid = l + r >> 1;
if(calc(mid) == oo) l = mid + 1; else r = mid;
}
// printf("st: %d %d\n", l, sum);
r = sum;
while(r - l > 1) {
int ml = l + (r - l) / 3, mr = ml + r >> 1;
// printf("[%d, %d] %d %d: %d %d\n", l, r, ml, mr, calc(ml), calc(mr));
if(calc(ml) < calc(mr)) r = mr;
else l = ml + 1;
}
printf("%d\n", min(calc(l), calc(r)));
fclose(stdin);
fclose(stdout);
return 0;
}A
试题描述
绿意盎然的一天,Scape去XX赛区加冕为王。
Scape倒开题目,看到了这样一道题:
有一个序列 \(A\) 和 \(L,R\),每次可以合并相邻的 \(K\) 个元素(要求 \(L \le K \le R\) ),代价为这 \(K\) 个元素的和并合并产生一个新元素,权值为这 \(K\) 个元素的和。
求把整个序列合并为一个元素的最小代价。
\(T\) 组数据,\(T \le 10, n \le 300\)。
Scape 想都不想就写了一个 \(n^4\) 暴力,结果居然 \(T\) 了,作为 XX 之王的 Scape 自然不会管这种辣鸡题,请你写出这道题。
输入
第一行一个整数 \(T(T \le 10)\),表示数据组数。
每组数据第一行三个整数 \(n,L,R\) 表示序列 \(A\) 的长度,和 \(K\) 的上下界限制。
第二行 \(n\) 个整数表示序列 \(A\)。
输出
每行一个整数表示结果,无解输出 \(0\)。
输入示例
3
3 2 2
1 2 3
3 2 3
1 2 3
4 3 3
1 2 3 4输出示例
9
6
0数据规模及约定
对于 \(20\%\) 的数据,\(n \le 20\)。
对于 \(60\%\) 的数据,\(n \le 50\)。
对于 \(100\%\) 的数据,\(n \le 300, A_i \le 100\)。
题解
还是倍增。
令 \(f(k, l, r)\) 表示对于 \([l, r]\) 中的所有数字,最后一步合并是 \(2^k\) 段合并在一起,其余的合并都是段数在 \([L, R]\) 之间的,最小代价。
\(g(k, l, r)\) 表示对于 \([l, r]\) 中的所有数字,最后一步合并为不超过 \(2^k\) 段合并在一起,其余的合并都是段数在 \([L, R]\) 之间的,最小代价。
那么这样就可以用 \(f(k, l, r)\) 组出 \(L\),然后再用 \(g(k, l, r)\) 组出 \(R - L\),就可以合并了。
为了方便合并,我们需要维护一个 \(F(k, l, r)\)。令 \(L\) 的二进制最低的 \(k\) 位组成的数位 \(x\),那么 \(F(k, l, r)\) 就是最后一步合并是 \(x\) 段合并在一起,其余的合并都是段数在 \([L, R]\) 之间的,最小代价。
同理,再维护一个 \(G(k, l, r)\)。令 \(R - L\) 的二进制最低的 \(k\) 位组成的数位 \(x\),那么 \(G(k, l, r)\) 就是最后一步合并为不超过 \(x\) 段合并在一起,其余的合并都是段数在 \([L, R]\) 之间的,最小代价。
这样将 \(F(maxb, l, r)\) 与 \(G(maxb, l, r)\) 的 dp 值再合并一下,就能得到区间 \([l, r]\) 的答案了。(\(maxb\) 表示二进制位数)
上面的合并都是指枚举中转点 \(i\),然后用 \(f_l(l, i) + f_r(i+1, r)\) 去更新 \(f_t(l, r)\),其中 \(f_l, f_r\) 指的是待合并的两个 dp 数组,\(f_t\) 指的是合并后的目标数组。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cassert>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
//#define DEBUG 233
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 310
#define maxlog 9
#define oo 2147483647
int n, L, R, S[maxn];
void upd(int& a, int b) {
if(a > b) a = b;
return ;
}
int f[maxlog][maxn][maxn], g[maxlog][maxn][maxn], F[maxlog][maxn][maxn], G[maxlog][maxn][maxn], vis[maxn][maxn];
void dp(int l, int r) {
if(l > r || vis[l][r]) return ;
vis[l][r] = 1;
if(l == r) {
f[0][l][r] = g[0][l][r] = 0;
if(L & 1) F[0][l][r] = 0;
if(R - L & 1) G[0][l][r] = 0;
rep(k, 1, maxlog - 1) {
upd(g[k][l][r], g[k-1][l][r]);
if(R - L >> k & 1) G[k][l][r] = 0;
upd(G[k][l][r], G[k-1][l][r]);
if(!(L >> k & 1)) upd(F[k][l][r], F[k-1][l][r]);
}
#ifdef DEBUG
rep(k, 0, maxlog - 1) printf("f[%d][%d][%d] = %d\n", k, l, r, f[k][l][r]);
#endif
return ;
}
rep(i, l, r) dp(l, i), dp(i + 1, r);
rep(k, 1, maxlog - 1) {
rep(i, l, r) {
if(i == r) assert(f[k-1][i+1][r] == oo);
if(f[k-1][l][i] < oo && f[k-1][i+1][r] < oo) upd(f[k][l][r], f[k-1][l][i] + f[k-1][i+1][r]);
if(g[k-1][l][i] < oo && g[k-1][i+1][r] < oo) upd(g[k][l][r], g[k-1][l][i] + g[k-1][i+1][r]);
if(L >> k & 1) {
if(f[k][l][i] < oo && F[k-1][i+1][r] < oo) upd(F[k][l][r], f[k][l][i] + F[k-1][i+1][r]);
}
else upd(F[k][l][r], F[k-1][l][r]);
if(R - L >> k & 1) {
if(g[k][l][i] < oo && G[k-1][i+1][r] < oo) upd(G[k][l][r], g[k][l][i] + G[k-1][i+1][r]);
}
upd(G[k][l][r], G[k-1][l][r]);
}
if((L & -L) == (1 << k)) upd(F[k][l][r], f[k][l][r]);
// printf("F[%d][%d][%d] = %d\n", k, l, r, F[k][l][r]);
}
rep(i, l, r) if(F[maxlog-1][l][i] < oo && G[maxlog-1][i+1][r] < oo)
upd(f[0][l][r], F[maxlog-1][l][i] + G[maxlog-1][i+1][r] + S[r] - S[l-1]);
upd(g[0][l][r], f[0][l][r]);
if(L & 1) F[0][l][r] = f[0][l][r];
if(R - L & 1) G[0][l][r] = g[0][l][r];
rep(k, 1, maxlog - 1) {
upd(g[k][l][r], g[k-1][l][r]);
if(R - L >> k & 1) upd(G[k][l][r], g[0][l][r]);
upd(G[k][l][r], G[k-1][l][r]);
if(!(L >> k & 1)) upd(F[k][l][r], F[k-1][l][r]);
}
#ifdef DEBUG
rep(k, 0, maxlog - 1) printf("f[%d][%d][%d] = %d\n", k, l, r, f[k][l][r]);
#endif
return ;
}
void work() {
n = read(); L = read(); R = read();
rep(i, 1, n) S[i] = read() + S[i-1];
memset(vis, 0, sizeof(vis));
rep(k, 0, maxlog - 1) rep(i, 1, n + 1) rep(j, 1, n + 1) {
f[k][i][j] = F[k][i][j] = oo;
g[k][i][j] = G[k][i][j] = i <= j ? oo : 0;
}
dp(1, n);
printf("%d\n", f[0][1][n] < oo ? f[0][1][n] : 0);
return ;
}
int main() {
freopen("A.in", "r", stdin);
freopen("A.out", "w", stdout);
int T = read();
while(T--) work();
fclose(stdin);
fclose(stdout);
return 0;
}B
试题描述
Scape 一到机房,所有做题的人便都看着他笑,有的叫道,“Scape,你一定又被标准分倍杀了!”他不回答,对柜里说,“测两个程序,看一眼成绩单。”便拷出两个程序。他们又故意的高声嚷道,“你怎么欧拉回路和逆序对都WA了!”……
Scape 知道,以上的故事只是 OI 生涯里的一个意外,为了证明自己,他决定教你 Border 的四种求法。
给一个小写字母字符串 \(S\),\(q\) 次询问每次给出 \(l,r\) ,求 \(s[l..r]\) 的 Border 。
Border: 对于给定的串 \(s\) ,最大的 \(i\) 使得 \(s[1..i] = s[|s|-i+1..|s|]\),\(|s|\) 为 \(s\) 的长度。
输入
第一行一个字符串 \(S\) 。
第二行一个整数 \(q\) 表示询问个数。
接下来的 \(q\) 行每行两个整数 \(l,r\) 表示一个询问。
输出
对于每组询问输出答案。
输入示例
abbabbaa
3
1 8
1 7
2 7输出示例
1
4
3数据规模及约定
对于 \(30\%\) 的数据,\(n,q \le 1000\)。
对于 \(50\%\) 的数据,\(n,q \le 20000\)。
对于另外 \(30\%\) 的数据,答案至少为 \(r-l+1\) 的一半。
对于 \(100\%\) 的数据,\(n,q \le 10^5\)。
题解
目前不会做
day4
神奇的钟点(time)
试题描述
一天,小 L 看到了 \(3\) 块钟表,分别显示着 \(01:08\)、\(03:40\)、\(13:52\)。小 L 发现,每块表上的时间都是 \(hh:mm\) 的形式,其中 \(hh\) 表示小时,\(mm\) 表示分钟,而且都不是整点(即 \(0 \le hh < 24, 1 \le mm < 60\))。
回想起小学数学老师刚刚讲的关于比例的知识,\(hh:mm\) 也表示一个比,它的值等于 \(\frac{hh}{mm}\)。这时小 L 发现了一件神奇的事情:把这三个钟点加起来会得到 \(18:40\),这也是一个不是整点的合法时间(注意小时数要小于 \(24\)),它对应的比值 \(\frac{9}{20}\) 与这三个钟点对应的比值 \(\frac{1}{8}\)、\(\frac{3}{40}\)、\(\frac{1}{4}\) 之和竟然相等!
现在小 L 想知道,把所有的满足这个神奇的性质的 \(3\) 个钟点组成的钟点组按照字典序排序后,第 \(k\) 小的是什么。
输入
输入只包含一个正整数 \(k\)。
输出
输出字典序第 \(k\) 小的满足题目所述神奇性质的钟点组,以一个空格隔开,详见样例输出。如果答案不存在,输出“\(-1\)”(不含引号)。
输入示例1
65432输出示例1
01:08 03:40 13:52输入示例2
1输出示例2
00:01 00:01 00:01输入示例3
58输出示例3
00:01 00:02 00:01输入示例4
2000000000输出示例4
-1数据规模及约定
对于 \(30\%\) 的数据,\(k \le 1000\)。
对于 \(60\%\) 的数据,\(k \le 20000\)。
对于 \(100\%\) 的数据,\(1 \le k \le 2 \times 10^9\)。
题解
分段打表、暴力剪枝均可。
(我是 \(1000\) 个打一次表,打表程序就是下面的程序改一下即可)
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
char Ans[130][50] = {
"00:01 00:01 00:01",
"00:01 00:22 00:13",
"00:02 00:07 00:26",
"00:02 00:35 00:04",
"00:03 00:15 00:28",
"00:04 00:02 00:25",
"00:04 00:26 00:29",
"00:05 00:10 00:29",
"00:05 00:57 17:34",
"00:06 00:21 00:31",
"00:07 00:07 00:22",
"00:07 00:47 00:02",
"00:08 00:19 00:32",
"00:09 00:06 00:13",
"00:09 00:53 01:02",
"00:10 00:19 00:17",
"00:11 00:06 00:27",
"00:11 01:08 00:57",
"00:12 00:23 00:11",
"00:13 00:07 00:20",
"00:13 08:42 08:56",
"00:14 00:33 00:06",
"00:15 00:16 00:28",
"00:16 00:03 00:31",
"00:16 04:08 06:54",
"00:17 00:26 00:07",
"00:18 00:15 00:16",
"00:19 00:02 00:02",
"00:19 05:50 06:15",
"00:20 00:45 01:05",
"00:21 00:14 00:12",
"00:22 00:05 00:27",
"00:22 12:57 05:19",
"00:23 05:45 07:18",
"00:24 02:26 00:49",
"00:25 00:17 00:02",
"00:26 00:08 00:02",
"00:27 00:03 00:05",
"00:27 13:44 03:33",
"00:28 07:49 00:39",
"00:29 07:15 03:36",
"00:30 05:30 06:36",
"00:31 02:16 00:37",
"00:32 03:12 05:40",
"00:33 01:30 07:42",
"00:34 01:52 01:26",
"00:35 02:30 05:15",
"00:36 03:24 15:32",
"00:37 03:15 12:40",
"00:38 08:32 00:26",
"00:39 11:33 04:12",
"00:40 11:22 10:20",
"00:42 00:06 00:10",
"00:43 00:19 05:10",
"00:44 02:20 04:16",
"00:45 07:18 10:09",
"00:47 00:03 00:07",
"00:48 03:08 10:20",
"00:49 16:32 01:06",
"00:51 02:08 12:16",
"00:53 00:03 00:02",
"00:54 09:18 00:08",
"00:56 08:48 00:10",
"00:59 00:05 10:40",
"01:03 08:32 03:45",
"01:06 09:54 07:33",
"01:10 10:50 05:40",
"01:15 02:45 15:36",
"01:20 03:45 08:15",
"01:25 00:38 00:47",
"01:30 14:45 01:30",
"01:44 00:22 05:22",
"02:04 00:39 11:34",
"02:08 11:26 07:52",
"02:14 00:46 04:21",
"02:20 01:30 11:55",
"02:24 13:36 06:36",
"02:32 03:36 04:24",
"02:40 03:20 09:30",
"02:55 14:40 00:09",
"03:08 01:24 00:40",
"03:15 01:36 16:45",
"03:21 00:58 00:09",
"03:30 03:30 08:35",
"03:36 18:40 01:24",
"03:50 03:15 02:20",
"04:08 00:37 00:25",
"04:15 05:24 03:45",
"04:22 00:40 07:22",
"04:30 07:35 02:30",
"04:40 01:14 00:41",
"04:48 10:24 00:18",
"05:09 02:18 00:45",
"05:18 03:45 14:15",
"05:30 00:11 01:57",
"05:40 00:28 04:32",
"05:52 02:13 09:15",
"06:12 00:41 14:28",
"06:22 00:27 08:44",
"06:32 12:24 02:32",
"06:44 00:24 07:14",
"07:05 00:45 12:20",
"07:16 02:04 07:56",
"07:28 02:32 07:32",
"07:42 00:18 13:48",
"07:55 02:20 00:29",
"08:15 05:20 03:45",
"08:30 03:33 02:30",
"08:48 00:12 04:54",
"09:10 01:05 00:55",
"09:27 06:09 00:40",
"09:45 02:15 09:36",
"10:10 00:37 04:26",
"10:25 01:30 07:35",
"10:40 05:30 07:20",
"11:11 00:25 00:36",
"11:35 02:56 00:09",
"12:12 00:12 00:49",
"12:32 01:40 04:15",
"12:52 07:26 00:22",
"13:32 03:36 04:24",
"14:14 00:45 00:16",
"14:49 04:35 02:16",
"15:36 00:35 01:01",
"16:32 00:40 04:06",
"17:44 00:37 03:12",
"19:14 01:04 02:56",
"22:44 00:25 00:37"
};
int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
void Nxt(int& a1, int& b1, int& a2, int& b2, int& a3, int& b3) {
b3++;
if(b3 < 60) return ;
b3 = 1; a3++;
if(a3 < 24) return ;
a3 = 0; b2++;
if(b2 < 60) return ;
b2 = 1; a2++;
if(a2 < 24) return ;
a2 = 0; b1++;
if(b1 < 60) return ;
b1 = 1; a1++;
return ;
}
int main() {
freopen("time.in", "r", stdin);
freopen("time.out", "w", stdout);
int n = read();
if(n > 127034) return puts("-1"), 0;
int cnt = n / 1000 * 1000; if(!cnt) cnt = 1;
char *str = Ans[n/1000];
int a1, b1, a2, b2, a3, b3;
sscanf(str, "%d:%d %d:%d %d:%d", &a1, &b1, &a2, &b2, &a3, &b3);
for(;; Nxt(a1, b1, a2, b2, a3, b3)) {
int tA = a1 + a2 + a3 + (b1 + b2 + b3) / 60, tB = (b1 + b2 + b3) % 60,
A = a1 * b2 * b3 + a2 * b1 * b3 + a3 * b1 * b2, B = b1 * b2 * b3;
if(tA >= 24) continue;
int g = gcd(tA, tB); tA /= g; tB /= g;
g = gcd(A, B); A /= g; B /= g;
if(tA == A && tB == B)
if(cnt++ == n) return printf("%02d:%02d %02d:%02d %02d:%02d\n", a1, b1, a2, b2, a3, b3), 0;
}
fclose(stdin);
fclose(stdout);
return 0;
}最长上升子序列(lis)
试题描述
现在有一个长度为 \(n\) 的随机排列,求它的最长上升子序列长度的期望。
为了避免精度误差,你只需要输出答案模 \(998244353\) 的余数。
输入
输入只包含一个正整数 \(n\)。
输出
输出只包含一个非负整数,表示答案模 \(998244353\) 的余数。
可以证明,答案一定为有理数,设其为 \(\frac{a}{b}\)(\(a\)、\(b\) 为互质的整数),你输出的整数为 \(x\),则你需要保证 \(0 \le x < 998244353\) 且 \(a\) 与 \(bx\) 模 \(998244353\) 同余。
输入示例1
1输出示例1
1输入示例2
2输出示例2
499122178输入示例3
3输出示例3
2数据规模及约定
对于 \(100\%\) 的数据,\(1 \le n \le 28\)。
共有 \(25\) 组数据,对于第 \(i\) 组数据(\(1 \le i\ le 25\)),\(n=i+3\)。
题解
状压 dp + 打表。考虑我们求最长上升子序列的过程,有一个 \(g\) 数组,\(g_i\) 表示长度为 \(i\) 的最长上升子序列的最后一位的最小值。那么我们的状态就维护这个数组。由于 \(g_i\) 一定是单调增的(由于没有重复元素),我们可以记录那些值出现在了 \(g\) 数组中。
于是 \(f(i, S)\) 表示填上了排列的前 \(i\) 位,\(g\) 数组中有集合 \(S\) 中的数的概率。转移的时候枚举最后一位填写哪个数字,假设填写了数字 \(k\),那么前 \(i\) 位中 \(\ge k\) 的数字都 \(+1\),不难发现这样做是正确的(形象地想象我们在原来的 \(1 \sim i\) 的排列中插入了数字 \(k\),那么 \(\ge k\)
的部分就都要腾出一个位置)。
由于 \(f(i, S)\) 的中的 \(S\) 最多有 \(2^i\) 种状态,所以状态数是 \(O(2^n)\) 的,转移数 \(O(n)\),所以总复杂度是 \(O(2^nn)\) 的。
打表程序:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <vector>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 30
#define maxs 268435456
#define MOD 998244353
#define LL long long
int n, inv[maxn], bit[maxs];
vector <int> f[maxn];
int main() {
bit[0] = 0;
rep(i, 1, maxs - 1) bit[i] = bit[i^(i&-i)] + 1;
inv[1] = 1;
rep(i, 2, maxn - 1) inv[i] = (LL)(MOD - MOD / i) * inv[MOD%i] % MOD;
printf("Ans[30] = {0, ");
rep(n, 1, 28) {
rep(i, 0, n) f[i].clear(), f[i].resize(1 << i);
f[0][0] = 1;
rep(i, 0, n - 1)
rep(s, 0, f[i].size() - 1) if(f[i][s])
rep(k, 0, i) {
int ls = s & ((1 << k) - 1), rs = (s >> k); rs -= rs & -rs;
int ts = ls | (rs << k << 1) | (1 << k);
f[i+1][ts] += (LL)f[i][s] * inv[i+1] % MOD;
if(f[i+1][ts] >= MOD) f[i+1][ts] -= MOD;
}
int ans = 0, x = 0;
rep(s, 0, f[n].size() - 1) if(f[n][s]) {
x += f[n][s]; if(x >= MOD) x -= MOD;
ans += (LL)bit[s] * f[n][s] % MOD;
if(ans >= MOD) ans -= MOD;
}
printf("%d%s", ans, n < 28 ? ", " : "};\n");
}
return 0;
}最终程序:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
int Ans[30] = {0, 1, 499122178, 2, 915057326, 540715694, 946945688, 422867403, 451091574, 317868537, 200489273, 976705134, 705376344, 662845575, 331522185, 228644314, 262819964, 686801362, 495111839, 947040129, 414835038, 696340671, 749077581, 301075008, 314644758, 102117126, 819818153, 273498600, 267588741};
int main() {
freopen("lis.in", "r", stdin);
freopen("lis.out", "w", stdout);
int n = read();
printf("%d\n", Ans[n]);
fclose(stdin);
fclose(stdout);
return 0;
}拓扑序列(topo)
试题描述
小 C 最近学习了拓扑排序的相关知识。对一个有向无环图 \(G\) 进行拓扑排序,是将 \(G\) 中所有顶点排成一个线性序列,使得对图 \(G\) 中任意一条有向边 \((u, v)\),\(u\) 在线性序列中出现在 \(v\) 之前。例如,如果图 \(G\) 的点集为 \(\{1, 2, 3, 4\}\),边集为 \(\{(1, 2), (1, 3), (2, 4), (3, 4)\}\),那么 \((1, 2, 3, 4)\) 和 \((1, 3, 2, 4)\) 都是图 \(G\) 的拓扑序列。
现在小 C 对一个简单(无重边)有向无环图进行了拓扑排序,但不小心把原图弄丢了。
除了拓扑序列,小 C 只记得原图的边数为 \(k\),而且图中存在一个顶点 \(u\) 可以到达其他所有顶点。他想知道有多少个满足上述要求的简单有向无环图。由于答案可能很大,你只需要输出答案模 \(m\) 的余数。
输入
输入第一行包含 \(3\) 个整数 \(n\)、\(k\)、\(m\)。
第二行是空格隔开的 \(n\) 个正整数 \(a_1, a_2, \cdots , a_n\),表示原图的一个拓扑序列,保证是 \(1\) 到 \(n\) 的一个排列。
输出
仅输出一个整数,表示满足要求的简单有向无环图个数模 \(m\) 的余数。
输入示例
4 4 4
1 2 3 4输出示例
1数据规模及约定
对于 \(100\%\) 的数据,\(0 \le k \le n \le 200000\),\(1 \le m \le 10^{200000}\)。
| 数据点编号 | $n \le$ | $m \le$ | 约束 |
|---|---|---|---|
| 1 - 2 | $5$ | $10^9$ | 无 |
| 3 | $10$ | $k = n - 1$ | |
| 4 - 5 | 无 | ||
| 6 | $200000$ | $k = n - 1$ | |
| 7 - 9 | 无 | ||
| 10 - 11 | $10^{500}$ | $k = n - 1$ | |
| 12 | 无 | ||
| 13 | $10^{18000}$ | $k = n - 1$ | |
| 14 | $10^{19000}$ | ||
| 15 | $10^{20000}$ | 无 | |
| 16 | $45000$ | $10^{200000}$ | $k = n - 1$ |
| 17 | $50000$ | ||
| 18 | $60000$ | 无 | |
| 19 | $150000$ | $10^{150000}$ | $k = n - 1$ |
| 20 | $180000$ | ||
| 21 | $200000$ | 无 | |
| 22 | $150000$ | $10^{200000}$ | $k = n - 1$ |
| 23 | $200000$ | ||
| 24 | $180000$ | 无 | |
| 25 | $200000$ |
题解
当 \(k = n - 1\) 时答案就是 \((n-1)!\);当 \(k = n\) 时设 \(f(i, 0)\) 表示前 \(i\) 个点,连接了 \(i-1\) 条边的方案数,\(f(i, 1)\) 表示前 \(i\) 个点,连接了 \(i\) 条边的方案数 dp 就好了。
丧心病狂高精度部分自动忽略
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 200010
#define LL long long
int n, k, MOD, f[maxn][2];
int main() {
freopen("topo.in", "r", stdin);
freopen("topo.out", "w", stdout);
n = read(); k = read(); MOD = read();
if(k < n - 1) return puts("0"), 0;
if(!k) {
if(MOD == 1) return puts("0"), 0;
return puts("1"), 0;
}
if(k == n - 1) {
int ans = 1;
rep(i, 1, n - 1) ans = (LL)ans * i % MOD;
printf("%d\n", ans);
}
else {
f[1][0] = 1;
rep(i, 2, n) {
f[i][0] = (LL)f[i-1][0] * (i - 1) % MOD;
f[i][1] = (LL)f[i-1][0] * (((LL)(i - 1) * (i - 2) >> 1) % MOD) % MOD + (LL)f[i-1][1] * (i - 1) % MOD;
if(f[i][1] >= MOD) f[i][1] -= MOD;
}
printf("%d\n", f[n][1]);
}
fclose(stdin);
fclose(stdout);
return 0;
}




















 3572
3572











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








