椭圆极点极线性质_椭圆，恁么美的焦点弦

专题：椭圆焦点弦

解析几何，对于许多学生来说，可能是倍觉无奈的。

仅计算量的问题，就凸显了自己的不足吧。

而且因为对图形性质的认识不足，在做题时就会显得底气不足，会常常因为知识的储备问题，备觉捉襟见肘。

所以，解析几何，知识的整理是必要的。

那么今天，

就讲讲椭圆的焦点弦。

当然，

双曲线与抛物线的焦点弦，

就自行脑补了。

【焦点弦】：

过椭圆、双曲线或抛物线焦点的弦

焦半径公式

① 直角坐标视角下的焦半径：

---

记住：和函数图像平移一样，左加右减哦。

---

② 极角坐标视角下的焦半径：

---

注意：左减右加，和上面的焦半径公式相哦！

③　两种视角下的焦点弦长：

极坐标视角下几个结论

① 通径：

两个简单性质：

①AM与椭圆相切 ② kBM=e，kAM=-e

---

② 焦半径倒数和：

---

③ 焦定比结论：

焦点分焦点弦的比值问题，称为焦定比问题，利用椭圆第二定义或极坐标方程，可以获知焦定比下的一组重要结论。

3焦点弦与切线

从上面的图像中，最少可以看出三个结论：

■过焦点弦的两端点分别作椭圆切线，

切线交点在准线上。

■过椭圆准线上任一点作椭圆两切线，

切点的连线过定点。

■垂直关系：PF1〦AB。

定点、定线的证明：

从上面的证明过程，

我们还可以得出一个重要的切点弦方程哦：

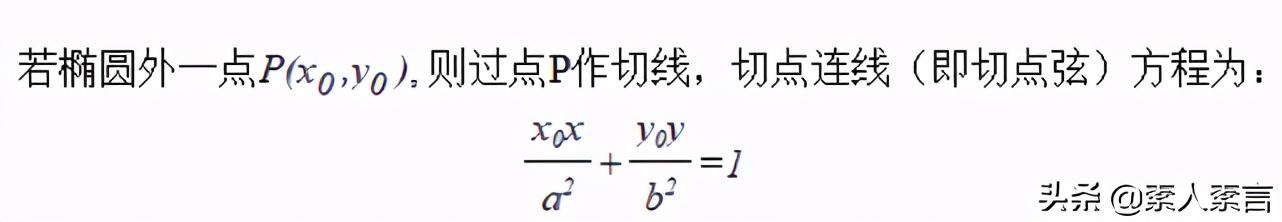
其实，根据切点弦方程，我们还可以大胆猜测：

只要动点P在一定直线上，

则切点弦所在直线一定过定点。

(观看视频验证结论)

点P和切点弦AB

就是传说中的极点和极线

有兴趣的你

是不是可以自己给自己编个题

来玩玩这个性质呢

垂直关系的证明可以这样：

圆锥曲线中的结论有许多，今天主要就焦点弦相关的几个常见结论做了部分讲解。

其实我认为，对类似这些结论做些研究，不仅便于我们加强对圆锥曲线性质的认识和理解，而且一些结论的证明过程，也包含了解析几何问题处理的常规思路，会让我们以后的解题更加理性和清晰。

当然，双曲线和抛物线中，相应的图形性质有很多是相似的，也需要我们去多比较、多总结，以提高我们解决解析几何问题的整体能力。

END