快速排序及其性能分析

QuickSort

• 快速排序算法是分治算法
• 快速排序是原地排序
• 在微调的情况下快速排序是非常实用的算法

Divide and conque

• Divide:选取合适的主元元素(pivot)将数组一分为二，divide结束后pivot左边的元素要小于等于pivot，右边的元素要大于pivot

• 再分别在子数组上利用递归来划分两个数组

• 最后合并

Running time

• 线性时间排序:

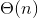
划分过程伪代码如下

    Partion(A,p,q)       //A[p,.....q]
    pivot <- A[p]
    i <- p
    for j <- p + 1 to q
        do if a[j] <= pivot
            i <- i + 1
            Exchange A[j] <-> A[i]
     Exchange A[i] <-> A[p]
     return i

• 算法描述

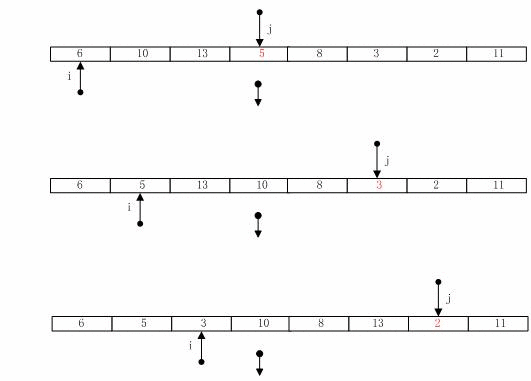
以上是一次划分的过程，再分别在两边递归划分，最后输入的数组的排序就完成了

快速排序的伪代码如下：

    QuickSort(A,p,q)
    if p < q
        r = Partition(A,p,q)
        QuickSort(A,p,r)
        QuickSort(A,r + 1,q)

以下是快速排序的动态过程：

快速排序的python实现可以移步至我的github去查看(QuickSort)

• 快速排序的算法复杂度分析

    

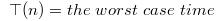
• **在最坏的划分下，每次划分完成时，pivot两边的子数组总有一边为0个元素，这时快速排序相当于插入排序，其递归式如下: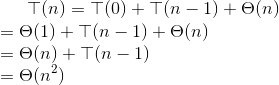

  

• 在最佳的划分下，每次划分之后 pivot正好位于数组中间

  

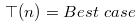
其递归式如下：

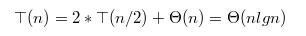
• 在更符合实际情况下我们假设划分的比例维持在1 ： 9的情况下，来计算快速排序的性能

其递归式如下：

由以上递归式可知其左子树的高度(T(n/10)的部分)会小于右子树(T(9n/10))的部分，所以

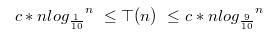
所以平均情况下快速排序的平均性能为，然而在现实生活中排序的情况要复杂的多，由于输入序列影响快速排序的性能，所以为了抵消由于输入序列而导致的性能问题，我们引入随机化的方法

• 随机快速排序

  • 其运行时间不依赖输入序列的顺序
  • 无需对输入序列的分布做任何假设
  • 不存在一种会输入序列会引起最差的运行效率
  • 最差的情况由随机数生成器确定

其伪代码如下

    Randomized-Parttion(A,p,q)
    i = Random(p,q)
    exchange A[i] <-> A[p]
    return Parttion(A,p,q) 

转载于:https://www.cnblogs.com/gcMerge/p/4778958.html