在数学中,ARG MAX(或ARGMAX)代表最大值,即给定参数的点集,给定表达式的值达到其最大值:
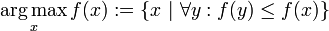
换一种说法,
是f(x)具有最大值M的x的值的集合。例如,如果f(x)是1- | x |,那么它在x = 0时达到其最大值1并且仅在那里, 所以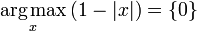 .
.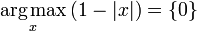 .
.
等价地,如果M是f的最大值,那么arg max是最大值的水平集
如果最大值达到一个值,那么一个将该点称为arg max,这意味着我们将arg max定义为一个点,而不是一组点。所以,例如
(而不是单独集合{5}),因为x(10-x)的最大值是25,这在x = 5时发生。 但是,如果在许多值处达到最大值,则arg max是一组点。 然后,我们举例说
![\underset{x \in [0,4\pi]}{\operatorname{arg\,max}} \, \cos(x) = \{0,2\pi,4\pi\}](http://upload.wikimedia.org/math/0/c/9/0c99d783a9fe097e42c3c38b2a1c0dd5.png)
因为cos(x)的最大值是1,当x =0,2π或4π时,这个间隔发生。在整个实线上,arg max是 
arg min(或argmin)被类似地定义.
还要注意函数通常不会达到最大值,因此通常不会有arg max: 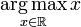 没有定义,因为x在实线上是无界的。然而,通过极值定理(或经典致密性理论),紧凑区间上的连续函数具有最大值,因此arg max。
没有定义,因为x在实线上是无界的。然而,通过极值定理(或经典致密性理论),紧凑区间上的连续函数具有最大值,因此arg max。
argmin 表示使目标函数取最小值时的变量值









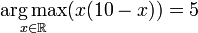













 6万+
6万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








