题目链接:https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1630
和挑战程序设计竞赛199页的题目几乎一样,将斐波那契数列的递推式表示成矩阵
我们把矩阵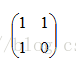
因此只要我们求出 A^n 就可以了。这就用到了矩阵快速幂。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
typedef long long ll;
typedef vector<int> vec; // 矩阵的一排
typedef vector<vec> mat; // 矩阵共有几排
const int maxn = 110010;
int mod;
mat mul(mat&A , mat&B){
mat C(A.size(),vec(B[0].size())); // A.size() :矩阵A排数,B[0].size() :矩阵B列数
for(int i=0;i<A.size();i++){
for(int k=0;k<B.size();k++){ // i k j;
for(int j=0;j<B[0].size();j++){
C[i][j] = C[i][j] + A[i][k]*B[k][j];
C[i][j] %=mod;
}
}
}
return C;
}
mat pow(mat A,int n){ //快速幂
mat B(A.size(),vec(A.size()));
for(int i=0;i<A.size();i++){ // 初始化为1;
B[i][i] = 1;
}
while(n > 0){
if(n & 1) B = mul(B,A);
A = mul(A,A);
n>>= 1;
}
return B;
}
int main(){
int a,b,n,m,T;
mat Mar(2,vec(2)); //构造函数 , 2个vec , 每个的值都是 vec(2);
scanf("%d",&T);
while(T--){
scanf("%d%d%d%d",&a,&b,&n,&m);
mod = 1;
while(m--) mod*=10;
Mar[0][0] = 1;
Mar[0][1] = 1;
Mar[1][0] = 1;
Mar[1][1] = 0;
Mar = pow(Mar,n-1); //求出n-1 则用 M[0][0] 和 M[0][1]对应的乘 F1 F0就可以了
printf("%d\n",(b*Mar[0][0] +a*Mar[0][1])%mod);
}
return 0;
}







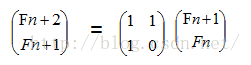
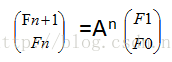














 2224
2224

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








