2010–2011, NEERC, Northern Subregional C.Commuting Functions

C.Commuting Functions 

 

由于要求答案字典序最小，我们肯定希望从g(1)开始对函数g进行赋值，于是又公式f(g(x))=g(f(x)) 设f(x)=i 我们推导出 

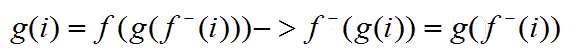
由于f是双射，当i逐个遍历1到n时 x也逐个遍历1到n

根据右边的公式，我们可以看出 当g的下标进行f-变换后 对应值也要进行f-变换 

回到f的value list 显然对于任意 f(a)=b 进行若干次f变换后 必有f(c)=a 也就是说 f的value list 是由若干个环组成的

每个环上都有唯一最小值， 且小环可以套到长度为其倍数的大环上

于是我们计算出f中所有长度环的最小值，并用长度小的环更新长度大的环 根据这个环的值对g从前往后赋值即可

代码很简单

#include<iostream>
#include<cstdio>
#include<cmath>
#include<vector>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int maxn=400000+5;
int f[maxn],ff[maxn],g[maxn],minn[maxn];
bool vis[maxn];
int main()
{//freopen("commuting.in","r",stdin);
 //freopen("commuting.out","w",stdout);
 int n;
 scanf("%d",&n);
 int les=-1;
 for(int i=1;i<=n;i++)
 	{
 	 scanf("%d",&f[i]);
 	 ff[f[i]]=i;
 	 g[i]=-1;
 	 vis[i]=0;
 	 minn[i]=-1;
	}
 for(int i=1;i<=n;i++)
 	{
 	 if(vis[i])continue;
 	 vis[i]=true;
 	 int nv=i,len=1,minv=i;
 	 while(ff[nv]!=i)
 	 	{

 	 	 nv=ff[nv];
 	 	 vis[nv]=true;
 	 	 len++;
		}
	 if(minn[len]==-1)minn[len]=i;
	 		else minn[len]=min(i,minn[len]);
	}
 for(int i=1;i<=n;i++)
 	{
 	 if(minn[i]==-1)continue;
 	 for(int j=i;j<=n;j+=i)
 	 	minn[j]=min(minn[j],minn[i]);
	}
 for(int i=1;i<=n;i++)
 	{
 	 if(g[i]!=-1)continue;
 	 int nv=i,len=1;
 	 while(ff[nv]!=i)
 	 	{
 	 	 nv=ff[nv];
 	 	 len++;
		}
	 
	 g[i]=minn[len];
	 
	 nv=i;
	 int val=g[i];
	 while(ff[nv]!=i)
	 	{
	 	 nv=ff[nv];
	 	 g[nv]=ff[val];
	 	 val=g[nv];
		}
	}
 for(int i=1;i<n;i++)
    printf("%d ",g[i]);
 printf("%d\n",g[n]);
 return 0;
}

　　通过这个题 增进了我对双射函数的理解。

 

转载于:https://www.cnblogs.com/heisenberg-/p/6715166.html