c实现三角形角度大于一个值_初三中考复习之解直角三角形：锐角三角函数1，学生可以自己复习...

第1课时 锐角三角函数(1)

一．课前预习

1. 直角三角形ABC中，∠C=90°，∠A=60°，∠B=_______°

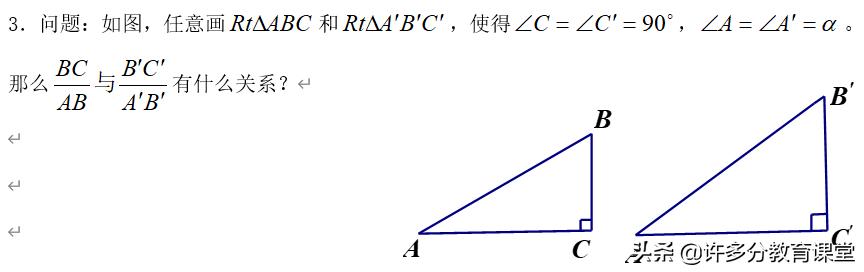
2. 直角三角形ABC中，∠C=90°，∠A=60°，AC=8，则AB=_______

3. 如图，△ABC中，AB=16，AC=4，则AC/AB=_______

二．师生互动，合作交流

1.问题：如图，直角三角形ABC中，∠C=90°，∠A=30°，BC=35m，求AB的长

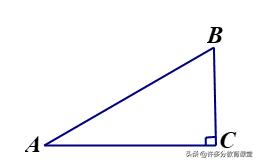
小结：在直角三角形中，30°角所对的边等于斜边的一半，即：

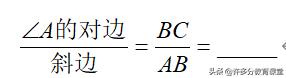
思考：在上面问题中，如果BC为50m，那么AB=_______

归纳：在一个直角三角形中，如果一个锐角等于30°，那么不管三角形的大小如何，这个角的对边与斜边的比值都等于1/2

2．问题：(1)如图，∠C=90°，∠A=45°，AC=2，计算∠A的对边与斜边的比BC/AB

(2)若AB=4，计算∠A的对边与斜边的比BC/AB

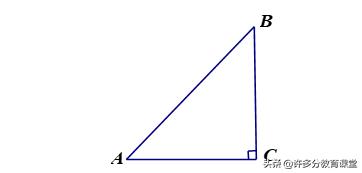
归纳：在一个直角三角形中，如果一个锐角等于45°，那么不管三角形的大小如何，这个角的对边与斜边的比值都等于√2/2.

归纳：1、在一个直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比都是一个______值

2、在Rt△ABC中，∠C=90°，我们把锐角A的对边与斜边的比叫做________，记作______, 即：

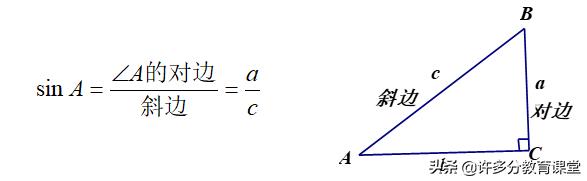
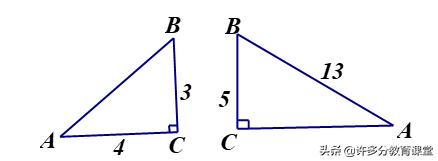
例1、如图，在Rt△ABC中，∠C=90°，求SinA和SinB的值

三．课堂练习

1、在Rt△ABC中，∠C=90°，AB=2，AC=1，则SinB的值是__________

2、在Rt△ABC中，∠C=90°，AB=5，AC=4，则SinA的值是__________

3、在Rt△ABC中，∠C=90°，AC=6，BC=8，则SinB=__________

4、Rt△ABC中，∠C=90°，BC=4，SinA=2/3，则AB=______，AC=_______

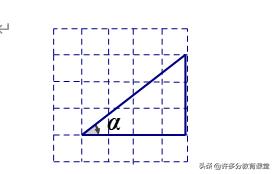
5、如图，三角形在正方形网格中的位置如图所示，则Sinα=( )

A、3/4 B、4/3 C、3/5 D、4/5

6、在直角三角形中，锐角A的对边与斜边的比值( )

A、小于0 B、大于1 C、可以等于1 D、大于0且小于1

7、在Rt△ABC中，∠C=90°，BC=2，SinA=2/3，则AC等于( )

A、√5 B、3 C、4/3 D、√13

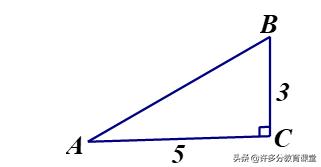
8、根据右图，求SinA和SinB的值

四．学习体会

通过今天的学习，我们应该掌握：

1. 锐角三角函数：∠A的正弦的概念

2. 固定角度的正弦是一个固定值

3．通过直角三角形的边长，求出某个锐角的正弦值

五．自我测试

1. 在Rt△ABC中，∠C=90°，AC=4，BC=3，则SinB的值是__________

2.在Rt△ABC中，∠C=90°，AB=10，AC=6，则SinA的值是__________

3.在Rt△ABC中，∠C=90°，AC=2，BC=2，则SinB=__________

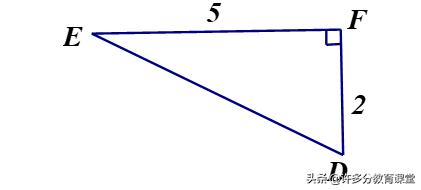
4.如图所示，求SinD和SinE的值

5、如图，在Rt△ABC中，∠ABC=90°，CD⊥AB，BC=5，CD=4，求SinA的值

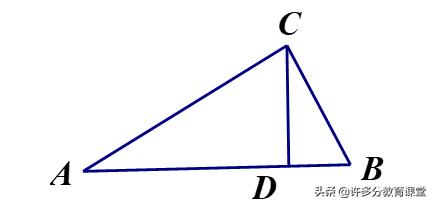
六．应用与拓展

如图所示，CD、BE是锐角三角形ABC的两条高，如果CD:BE=3:2，求Sin∠ABC:Sin∠ACB的值

欢迎关注@许多分教育课堂，之后会上传本节课的视频课，敬请关注！