那些教材中未给出证明的定理,到底能否使用?

初中几何知识体系,是基于《几何原本》中的公理体系建立的,可以看作是公理体系的子集,在教材编写中,为了教学方便,并没有直接照搬,而是有选择性地“重建”了一套公理体系,原本许多定理,在教材中被称为公理。
教材中的几何十大公理:1.过两点有且只有一条直线.2.两点之间,线段最短.3.垂线段最短.4.过一点有且只有一条直线与已知直线垂直.5.过直线外一点有且只有一条直线与已知直线平行.(平行公理)6.同位角相等,两直线平行.7.有两边及其夹角对应相等的两个三角形全等.(SAS)8.有两角及其夹边对应相等的两个三角形全等.(ASA)9.三边对应相等的两个三角形全等.(SSS)10.斜边和一条直角边对应相等的两个直角三角形全等.(HL)
公理体系便以这十条公理为基础,先证明一批真命题作为定理,再以这些定理为基础证明一批推论,这些公理、定理、推论便构成了我们整个初中几何证明体系。既然是公理体系,那么便要遵循体系规则,按教材安排的前后顺序进行教学,原则上凡是能成为证明依据的定理,需要首先用已知结论证明。
到了九年级中考复习阶段,基本已经完成了所有定理的证明,那么综合题中,学生可使用的范围便不再受限制,可自由使用。但是受教材知识结构限制,有一部分真命题,从最早期的定理沦落成命题,那么这些真命题,能否在考试中作为依据出现?一直是复习课教学中引发争论的地方。
争论一
定理:直角三角形中,30°角所对的直角边等于斜边的一半。出现位置在人教版八年级上册,其实它有一个逆命题:直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的角为30°。
我们可以对它的正确性进行必要的证明,如下图:
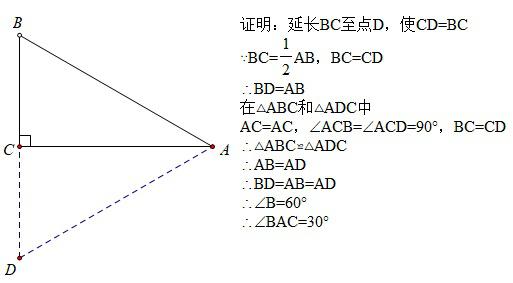
根据它出现的教材位置,可以使用八年级的知识进行证明,因此,在体系中,它有资格成为一个定理。可惜的是,在教材中,它并不是,只能作为一个真命题出现。
而在学习了三角函数之后,它的证明又更进一步简化了,根据直角边与斜边的比值,得到对角的正弦值,从而也能得到30°角。
争论二
定理:直角三角形中,斜边上的中线等于斜边的一半。它也有一个逆命题,同样为真命题,三角形中,如果某边上的中线等于这条边的一半,则这个三角形是直角三角形。
我们同样可以对它的正确性进行证明,如下图:
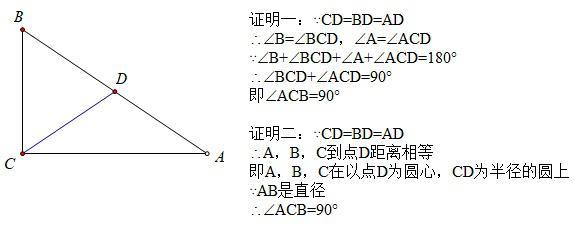
根据该定理出现的教材位置,用证明一可以完成证明,或者在中考复习中用证明二完成,它也是一个真命题。
争论三
定理:在同圆或等圆中,同弧所对的圆周角是圆心角的一半;同弧所对的弦相等;相等的弧所对的圆心角相等。
后来教材中进行了归纳,同圆或等圆中,圆心角、圆周角、弧、弦四组量中只要有一组量相等,剩下三组量均相等。再往后学习了弦心距之后,再加上它,总共五组量,简称为“五合一”,这五组量之间的关系同样也能证明为真命题。那么补充进来的几组量可以作为证明依据使用吗?
争论四
圆的垂径定理中,可由垂直于弦的直径得到两个结论,直径平分这条弦、直径平分弦所对的弧;也可由平分弦(不是直径)的直径得到两个结论,直径垂直于弦、直径平分弦所对的弧。那么,由直径平分弦所对的弧,其实也能得到直径垂直于弦、直径平分这条弦,如下图:

也就是说,垂径定理中的三个条件,任意一个可以得到另外两个。
以上四种争论,其实归根到底就是究竟学生在解几何综合题时,到底能否将之作为依据。
原则上,不能。
根据教材要求,也仿照公理化体系,未经证实的结论,不可作为定理直接用,但如果要使用,可先将这个命题证明一次,再利用它的结论,这样是符合教材要求的。
而在实际教学中,学生真要书写这些过程,无疑将使解答时间大大延长,对于中考120分钟的时间限定,是一大挑战,于是,在某些时候,我们默认了学生“省”步骤的做法。但作为老师,还是要有原则,不妨碍主体证明思路的步骤,省了可以,但涉及到主线思维中的关键步骤,不能省。在使用证明依据时,未经教材注明为定理的依据,不能直接使用,而是要先简要说明。
疑惑依然存在,如果在中考时,题目过程较多,那是否又可以使用上述“定理”呢?我想首先应从命题角度出发,从源头上避免证明步骤较多的情况,其次,避开有可能用到上述“定理”的条件,最后,本着人文关怀的理念,阅卷过程中,发现用到了这些定理的,不用挑刺的眼光看待。
举报/反馈





















 1124
1124











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








