java 树 最短路径代码_算法系列笔记8(有关图的算法二—最短路径问题)

结果如下：

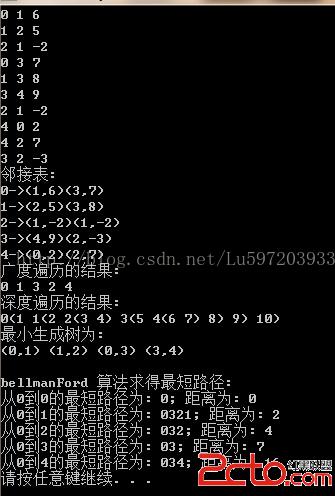
时间复杂度为O(VE).

注意：这里有个应用就是差分约束系统。其实线性规划的一种特殊情况，即A矩阵每行只有一个1和-1，其它的都为0，这样可以构造约束图，求得最短路径就是差分约束系统的解。这里不详细介绍了。

DAG图的单源最短路径

算法的基本思想：求DAG图的拓扑排序，然后按照拓扑排序顶点的顺序对其每条边进行松弛操作即如果d[v] > d[u]+w[u,v]，则d[v] = d[u]+w[u,v]。其时间复杂度为O(V+E).

二：全对最短路径问题

求所有的两两顶点之间的最短路径，最基本的思想就是对所有的顶点都运用单源最短路径问题。这样当无权值时，时间复杂度为O(V^2+VE);权值非负为O(V^2lgV+VE);一般情况为O(V^2*E),此时对于稠密图E=O(V^2)，要达到O(V^4)了，效率会非常差，因此需要其他算法来改进时间复杂度。主要有三种方法，第一种为动态规划方法(结合矩阵乘法)；第二种为Floyd-Warshall算法；第三种为Johnson算法，对于稀疏图要优于Floy-Warshall算法。

动态规划方法

其中dijm表示从i到j的最短路径，其中最多经过m条边。此时当m=V-1即为我们要求的最短路径(对于无负权环)。D(1)=W为权重矩阵。即求D(V-1).

此外将(1)式看做某种新运算*，那么每次都是求D(m) = D(m-1) * W。

代码如下：

// 用动态规划求全最短路径

void Graph::dpAllDistance(){

int Adj[maxSize][maxSize];

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

minAllDistance[i][j] = MAXPRICE;

if(i == j) minAllDistance[i][j] = 0;

AllPath[i][j] = intToStr(i);

Adj[i][j] = minAllDistance[i][j];

}

}

for(int i = 0; i < vertexNum; i++){

GNode *p = edges[i].next;

while(p != NULL){

minAllDistance[i][p->val] = p->weight; // 经过了1条边 即为权重

Adj[i][p->val] = p->weight;

AllPath[i][p->val] = AllPath[i][p->val] + intToStr(p->val);

p = p->next;

}

}

for(int m = 2; m < vertexNum; m++){ // 至多经过m条边

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

for(int k = 0; k < vertexNum; k++){

if(minAllDistance[i][j] > minAllDistance[i][k] + Adj[k][j]){

minAllDistance[i][j] = minAllDistance[i][k] + Adj[k][j];

AllPath[i][j] = AllPath[i][k] + intToStr(j);

}

}

}

}

}

// 检测是否存在负权环

for(int i = 0; i < vertexNum; i++){

if(minAllDistance[i][i] < 0){

cout << "该图存在负权环" << endl;

return;

}

}

// 将全对最短路径输出

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

cout << "从" <

时间复杂度：此时时间复杂度仍然为O(V^4)，但是采用D(m) = D(m/2)*D(m/2)来计算，时间复杂度即为O(V^3*lgV).

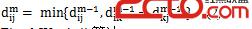
Floyd-Warshall算法

定义dijk表示从i到j考虑了从中间节点{1,2,3…k}经过的所有情况的最小值。当k=n时，即考虑了所有顶点，此时即为最短路径。

代码如下：

// floyd-warshall算法求最短路径问题

void Graph::floydWarshall(){

int Adj[maxSize][maxSize];

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

minAllDistance[i][j] = MAXPRICE;

if(i == j) minAllDistance[i][j] = 0;

AllPath[i][j] = intToStr(i);

Adj[i][j] = minAllDistance[i][j];

}

}

for(int i = 0; i < vertexNum; i++){

GNode *p = edges[i].next;

while(p != NULL){

minAllDistance[i][p->val] = p->weight; // 经过了1条边 即为权重

Adj[i][p->val] = p->weight;

AllPath[i][p->val] = AllPath[i][p->val] + intToStr(p->val);

p = p->next;

}

}

for(int k = 0; k < vertexNum; k++){

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

if(minAllDistance[i][j] > minAllDistance[i][k] + minAllDistance[k][j]){

minAllDistance[i][j] = minAllDistance[i][k] + minAllDistance[k][j];

AllPath[i][j] = AllPath[i][k] + AllPath[k][j];

}

}

}

}

// 检测是否存在负权环

for(int i = 0; i < vertexNum; i++){

if(minAllDistance[i][i] < 0){

cout << "该图存在负权环" << endl;

return;

}

}

// 将全对最短路径输出

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

cout << "从" <

结果如下：

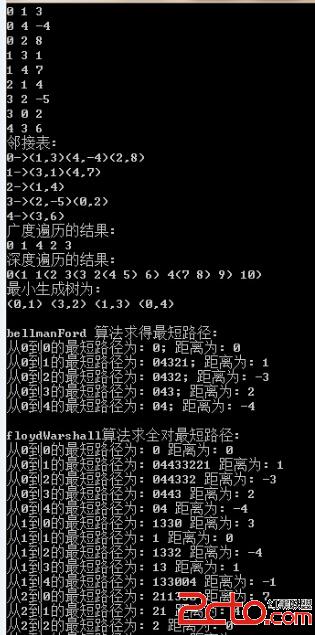
时间复杂度为O(V^3).

Johnson算法

Johnson算法采用了重赋权重方法。重赋权重方法不会改变最短路径，此外通过重赋权重产生的都是非负权重。

伪代码：

时间复杂度为O(V)*Dijkstra算法。

算法全部代码：

graph.h

#ifndef GRAPH_H

#define GRAPH_H

#include #include #include #include #include using namespace std;

#define maxSize 10

#define MAXPRICE 0x10000000 // 将此值设为权值的最大值

struct GNode{

int val;

int weight;

GNode *next;

};

class Graph{

public:

void createGraph(int n, int e);

void destroyGraph(GNode *p);

~Graph(){

for(int i = 0; i < vertexNum; i++){

destroyGraph(edges[i].next);

//cout << "析构:" << i << endl;

}

}

void showGraph();

void bfsTravel(); // 广度遍历

void dfsTravel(); // 深度遍历

void showTopSort(); // 输出拓扑序列

void componentSC(); // 建立图g的强连通分量

void prim();

void dijkstra();

void bellmanFord();

// 动态规划求全最短路径

void dpAllDistance();

void floydWarshall();

private:

int vertex[maxSize]; // 存放顶点

GNode edges[maxSize]; // 存放邻接表

int vertexNum; //顶点个数

int edgesNum; //边条数

//bfs and dfs 遍历

int visited[maxSize];

void bfs(int s);

void dfs(int s);

int beginTime[maxSize]; // 深度开始访问x的时间

int endTime[maxSize]; // 结束访问x的时间

static int time;

vectortopSort; // topSort的逆序为有向无回路的拓扑排序

void buildTransGraph(Graph &g); // 建立图g的转置

// prim

mapmPriceQueue; // 保存最小生成树和dijkstra算法的造价

pairgetMinPriceVet();

int preNode[maxSize]; // 用于保存最小生成树的边 值为该结点的前驱

// 保存dijkstra 路径

string path[maxSize]; // 保存最终的最短路径

int minDistance[maxSize]; // 保存最终的最小距离

string intToStr(int i);

// 保存所有路劲

int minAllDistance[maxSize][maxSize];

string AllPath[maxSize][maxSize];

};

#endifgraph.cpp

#include #include "graph.h"

#include #include #include using namespace std;

int Graph::time = 0;

void Graph::createGraph(int n, int e){

vertexNum = n;

edgesNum = e;

for(int i = 0; i < n; i++){

vertex[i] = i;

edges[i].val = i;

edges[i].weight = 0;

edges[i].next = NULL;

}

for(int i = 0; i < e; i++){

int source, dest, wei;

cin >> source >> dest >> wei;

GNode *newNode = new GNode();

newNode->val = dest;

newNode->weight = wei;

newNode ->next = NULL;

GNode *p = &edges[source];

while(p->next != NULL) p = p->next;

p->next = newNode;

// 无向图 有向图就将这段删除掉

/*GNode *newNode2 = new GNode();

newNode2->val = source;

newNode2->weight = wei;

newNode2 ->next = NULL;

GNode *p2 = &edges[dest];

while(p2->next != NULL) p2 = p2->next;

p2->next = newNode2;*/

}

}

void Graph::destroyGraph(GNode *p){

if(p == NULL) return;

else{

destroyGraph(p->next);

delete p;

}

}

void Graph::showGraph(){

for(int i = 0; i < vertexNum; i++){

int j = i;

cout << i << "->";

GNode *p = edges[j].next;

while( p != NULL) {

cout << "(" << p->val

p = p->next;

}

cout << endl;

}

}

// 广度遍历图

void Graph::bfs(int s){

queueq;

q.push(s);

visited[s] = 1;

while(!q.empty()){

int u = q.front();

q.pop();

cout << u

q.push(p->val);

visited[p->val] = 1;

}

p = p->next;

}

}

}

void Graph::bfsTravel(){

memset(visited, 0, sizeof(int)*vertexNum);

for(int i = 0; i < vertexNum; i++){

if(!visited[i]){

bfs(i);

cout << endl;

}

}

}

// 深度优先遍历

void Graph::dfs(int s){

visited[s] = 1;

time += 1;

beginTime[s] = time;

cout << s << "(" << beginTime[s] << " "; // shen

GNode *p = edges[s].next;

while(p != NULL){

if(!visited[p->val])

dfs(p->val);

p = p->next;

}

time += 1;

endTime[s] = time;

topSort.push_back(s);

cout << endTime[s] << ")" <::reverse_iterator iter="topSort.rbegin();" topsort.rend>

cout << *iter << " ";

cout << endl;

}

// 创建图g的转置

void Graph::buildTransGraph(Graph &g){

this->vertexNum = g.vertexNum;

this->edgesNum = g.edgesNum;

for(int i = 0; i < vertexNum; i++){

this->vertex[i] = g.vertex[i];

this->edges[i].val = g.edges[i].val;

this->edges[i].weight = g.edges[i].weight;

this->edges[i].next = NULL;

}

for(int i = 0; i < vertexNum; i++){

GNode *p = g.edges[i].next;

while(p != NULL){

GNode *newNode = new GNode();

newNode->val = i;

newNode->next = NULL;

newNode->weight = p->weight;

GNode *q = &edges[p->val];

while(q->next != NULL) q = q->next;

q->next = newNode;

p = p->next;

}

}

}

//强连通分量

void Graph::componentSC(){

//time = 0;

//dfsTravel(); // 对图g进行深度搜索得到完成x访问所需要的时间 并由此得到其拓扑排序

Graph g2;

g2.buildTransGraph(*this); // 得到图G的转置

time = 0;

memset(g2.visited, 0, sizeof(int)*vertexNum);

cout << "强连通分量: " << endl;

for(vector::reverse_iterator iter = topSort.rbegin(); iter != topSort.rend(); iter++){ // 对转置图g2进行深度搜索得到强连通分量

if(!g2.visited[*iter])

g2.dfs(*iter);

}

cout << endl;

}

// 最小生成树

/*最小生成树采用的是贪心算法：设T是图G的MST(minimum spanning tree),

A属于V， (u,v)是连接A与V-A之间的一条边且权值最小，则(u,v)边属于最小生成树

lowcost存放代价*/

pairGraph::getMinPriceVet(){

pairp;

int minPrice = MAXPRICE;

int minPriceVet = 0;

for(map::iterator iter = mPriceQueue.begin(); iter != mPriceQueue.end(); iter++){

if((*iter).second < minPrice){

minPrice = (*iter).second;

minPriceVet = (*iter).first;

p = *iter;

}

}

mPriceQueue.erase(minPriceVet); // 或者采用数组 此时就需要设置visited标记数组来判断该顶点是否已经加入S中了

return p;

}

void Graph::prim(){

mPriceQueue.clear();

mPriceQueue[0] = 0;

for(int i = 1; i < vertexNum; i++){

mPriceQueue[i] = MAXPRICE;

}

while(!mPriceQueue.empty()){

pairpMinNode = getMinPriceVet();

int minPriceVet = pMinNode.first;

GNode *p = edges[minPriceVet].next;

while(p != NULL){

if(mPriceQueue.count(p->val) && p->weight < mPriceQueue[p->val]){

mPriceQueue[p->val] = p->weight;

preNode[p->val] = minPriceVet;

}

p = p->next;

}

}

// 展示最小生成树的边

for(int i = 1; i < vertexNum; i++)

{

cout << "(" << preNode[i] << "," << i << ") ";

}

cout << endl;

}

// dijkstra 算法

string Graph::intToStr(int i){

string s;

stringstream ss;

ss << i;

ss >>s;

ss.clear();

return s;

}

void Graph::dijkstra(){

mPriceQueue.clear();

mPriceQueue[0] = 0;

path[0] = intToStr(0);

for(int i = 1; i < vertexNum; i++){

mPriceQueue[i] = MAXPRICE;

path[i] = "";

}

while(!mPriceQueue.empty()){

pairpMinNode = getMinPriceVet(); // dijkstra的贪心策略就是该点就是此时的pMinNode.second就是最短路径

int minPriceVet = pMinNode.first;

minDistance[minPriceVet] = pMinNode.second; // 保存最短路径到minDistance中

GNode *p = edges[minPriceVet].next;

while(p != NULL){

if(mPriceQueue.count(p->val) && (p->weight + pMinNode.second) < mPriceQueue[p->val]){ // 松弛操作

mPriceQueue[p->val] = p->weight + pMinNode.second;

path[p->val] = path[minPriceVet] + intToStr(p->val);

}

p = p->next;

}

}

// 输出路径

for(int i = 0; i < vertexNum; i++){

cout << "从0到" << i << "的最短路径为: " p->weight + minDistance[i]){ // 松弛每一条边

minDistance[p->val] = minDistance[i] + p->weight;

path[p->val] = path[i] + intToStr(p->val);

}

p = p->next;

}

}

}

for(int i = 0; i < vertexNum; i++){ // 检查是否存在负权回路

GNode *p = edges[i].next;

while(p != NULL){

if(minDistance[p->val] > p->weight + minDistance[i]){

cout << "该图存在负权环" << endl;

return;

}

p = p->next;

}

}

// 输出路径

for(int i = 0; i < vertexNum; i++){

cout << "从0到" << i << "的最短路径为: " weight; // 经过了1条边 即为权重

Adj[i][p->val] = p->weight;

AllPath[i][p->val] = AllPath[i][p->val] + intToStr(p->val);

p = p->next;

}

}

for(int m = 2; m < vertexNum; m++){ // 至多经过m条边

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

for(int k = 0; k < vertexNum; k++){

if(minAllDistance[i][j] > minAllDistance[i][k] + Adj[k][j]){

minAllDistance[i][j] = minAllDistance[i][k] + Adj[k][j];

AllPath[i][j] = AllPath[i][k] + intToStr(j);

}

}

}

}

}

// 检测是否存在负权环

for(int i = 0; i < vertexNum; i++){

if(minAllDistance[i][i] < 0){

cout << "该图存在负权环" << endl;

return;

}

}

// 将全对最短路径输出

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

cout << "从" weight; // 经过了1条边 即为权重

Adj[i][p->val] = p->weight;

AllPath[i][p->val] = AllPath[i][p->val] + intToStr(p->val);

p = p->next;

}

}

for(int k = 0; k < vertexNum; k++){

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

if(minAllDistance[i][j] > minAllDistance[i][k] + minAllDistance[k][j]){

minAllDistance[i][j] = minAllDistance[i][k] + minAllDistance[k][j];

AllPath[i][j] = AllPath[i][k] + AllPath[k][j];

}

}

}

}

// 检测是否存在负权环

for(int i = 0; i < vertexNum; i++){

if(minAllDistance[i][i] < 0){

cout << "该图存在负权环" << endl;

return;

}

}

// 将全对最短路径输出

for(int i = 0; i < vertexNum; i++){

for(int j = 0; j < vertexNum; j++){

cout << "从" <