两向量点乘坐标运算_三个视频搞定平面向量（坐标篇）：平面向量的正交分解、线性运算的坐标表示、平行向量的坐标表示、...

引导：高一、高三一轮复习阅读

● 本文适合高一学生预习与章节复习时阅读，也适合高三学生一轮复习时阅读；

● 阅读时建议先看视频，再读文字；

● 看视频时注意及时暂停，深入思考，步步为营，理解透彻。

学习向量的坐标表示，首先要理解向量坐标产生的原理，其次是练熟向量坐标运算的规则。

01

平面向量的正交分解

视频：平面向量的正交分解与坐标表示

1、把一个向量分解为两个互相垂直的向量，叫做把向量正交分解。

2、平面向量的坐标

(1)在平面直角坐标系中，分别取与x轴、y轴方向相同的两个单位向量　i、j作为基底.对于平面内的一个向量a，由平面向量基本定理可知，有且只有一对实数x，y，使得a＝xi＋yj.平面内的任一向量a都可由x、y唯一确定，我们把有序数对(x，y)叫做向量a的坐标，记作a＝(x，y).

(2)在平面直角坐标平面中，i＝(1，0)，j＝(0，1)，0＝(0，0).

02

平面向量的坐标表示举例、坐标运算

视频：平面向量坐标表示举例、坐标运算讲解

3、平面向量的坐标

即任意一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。

4、平面向量的坐标运算规则。

5、应用举例

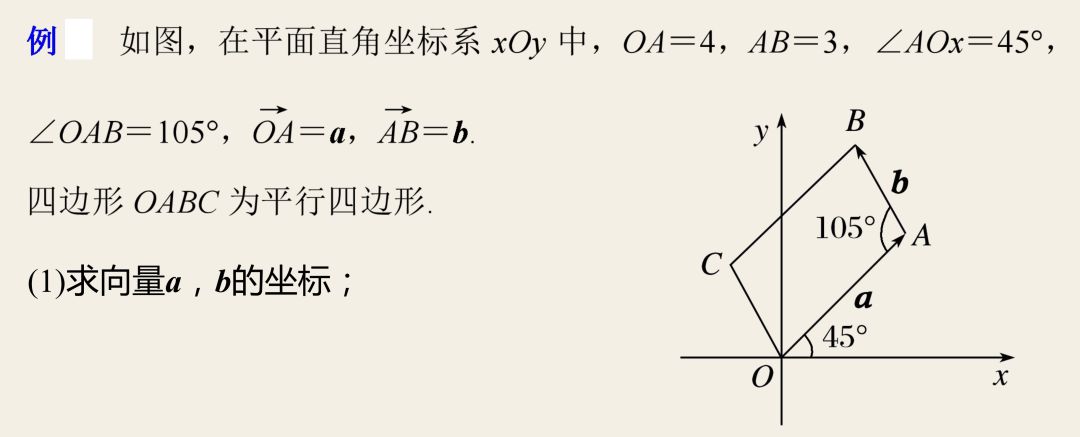
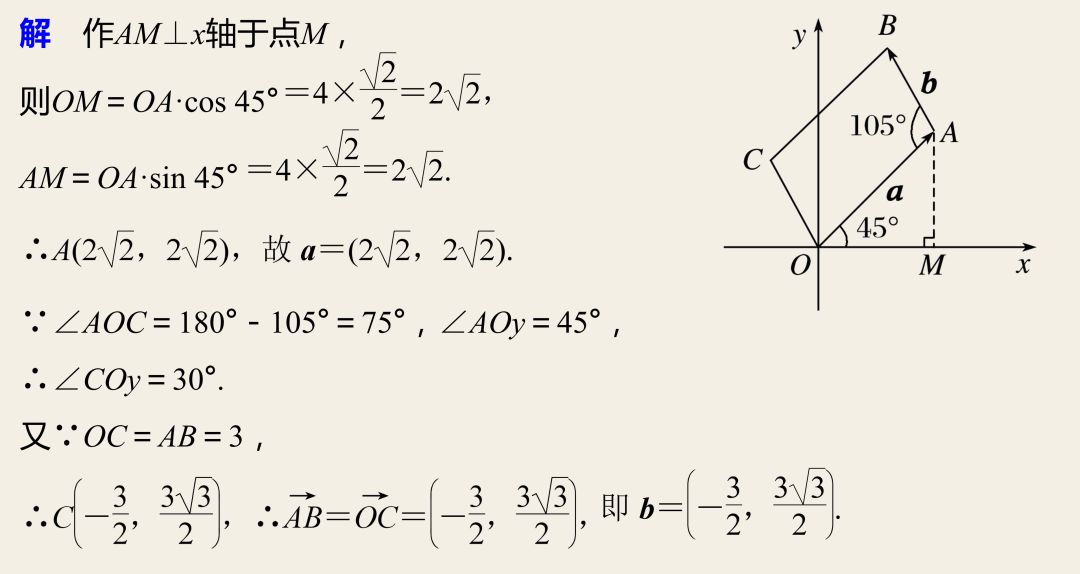
在表示点、向量的坐标时，可利用向量的相等、加减法运算等求坐标，也可以利用向量、点的坐标定义求坐标.。

向量坐标运算的方法

(1)若已知向量的坐标，则直接应用两个向量和、差及向量数乘的运算法则进行.

(2)若已知有向线段两端点的坐标，则可先求出向量的坐标，然后再进行向量的坐标运算.

(3)向量的线性坐标运算可完全类比数的运算进行。

03

平行向量的坐标表示

视频：平行向量的坐标表示

6、平行向量的坐标表示

7、应用举例

根据向量共线条件求参数问题，一般有两种思路，

一是利用向量共线 定理a＝λb(b≠0)，列方程组求解，

二是利用向量共线的坐标表达式 x1y2－x2y1＝0求解.

(1)三点共线问题的实质是向量共线问题，两个向量共线只需满足方向相 同或相反，两个向量共线与两个向量平行是一致的，利用向量平行证明 三点共线需分两步完成：①证明向量平行；②证明两个向量有公共点.

(2)若A，B，C三点共线，即由这三个点组成的任意两个向量共线。

人生有缘才相遇 扫码相识更有趣

        人生有缘

        扫码相识

        视频学习

        天然有趣