圆的相切相交相离公式_圆的完美终结篇

转载是一种动力 分享是一种美德

一直以来，

总是热衷于圆锥曲线的总结，

却忽视了对圆锥曲线初始内容，

圆的相关知识的整理。

也可能仅仅是觉得比较简单吧。

但作为圆锥曲线的初始内容，

课堂上，

我其实真的是很重视，

很重视圆的内容教学的。

不过，

应网友的要求，

今天还是决定写个圆的系统知识总结。

圆的形状

---

学了好长时间的椭圆了，

是不是都快忘记圆是什么样了呢？

其实，

圆与椭圆之间的关系是非常简单的，

看看下面这个图，

基本就能很直观的理解了。

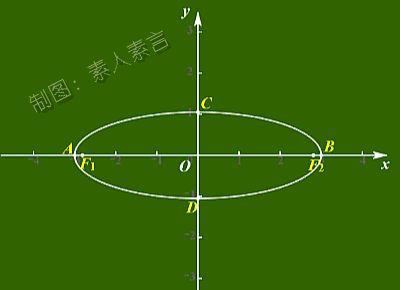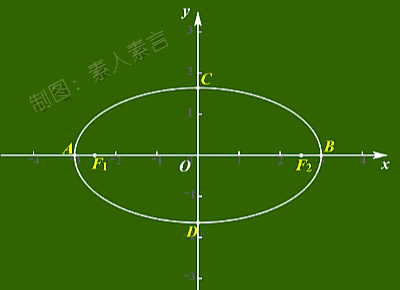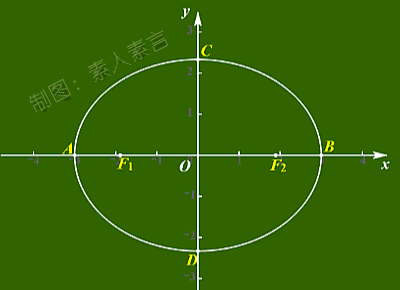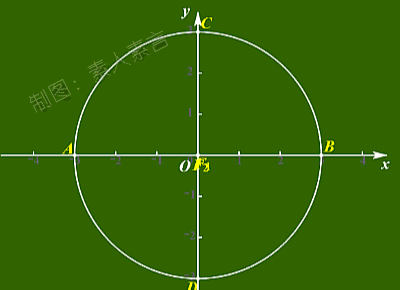
你是不是也看出了点什么呢？

原来，

当椭圆两焦点在无限接近的过程中，

椭圆会慢慢变得更圆了。

一直到F₁F₂=0时，

真的就变成了一个圆。

所以有时也说，

圆是当离心率为0时，

一个特殊的椭圆。

原来，

圆只是椭圆的一个极端情形。

两个要素

---

除了圆心和半径，

圆还有两个基本要素，

周长和面积。

显然，

圆的大小由它的半径决定，

所以圆的周长与面积，

都是关于半径的表达式。

圆的周长：l=2πr

1

圆的面积：S=πr²

你能从图中看出，

为什么圆的面积是πr²么？

其实，

按照动画的思路，

将圆无数次分割再拼接，

是一定能得到一个平行四边形的。

它的底边是半圆展开的长度πr，

高显然便是圆的半径了。

这样的结果，

圆的面积是不是就是πr²呢！

当然，

也不要太过于较真了，

因为这里用到了极限的感觉，

如果细究起来，

现在倒也真的是没办法解释的。

三个定义

---

定义一：

---

平面内到一定点距离为定值的点的集合。

上面那个，

是圆的静态定义。

但如果看到了下面这个动图，

是不难看出圆的另一个动态的定义的。

定义二：

---

将线段绕其一个端点旋转360°， 

另一端点的轨迹是圆。

其实，

除了这两个定义之外，

圆还有一个让人难忘的定义。

那当然就是，

最好用的阿氏圆，

全称“阿波罗尼斯圆”了。

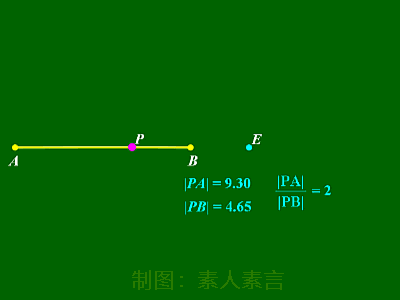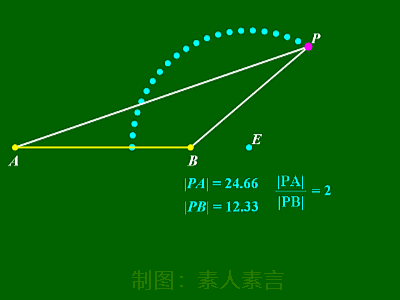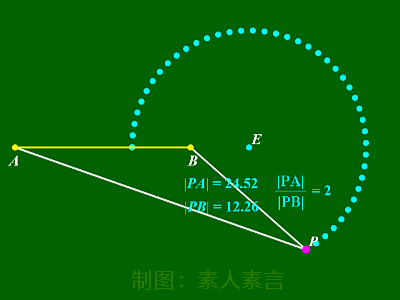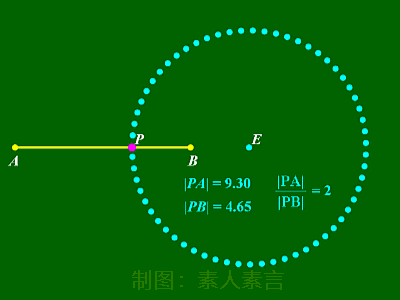
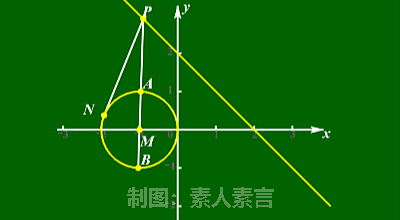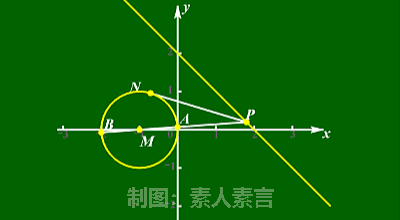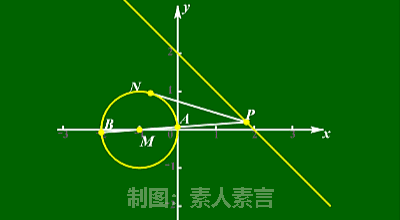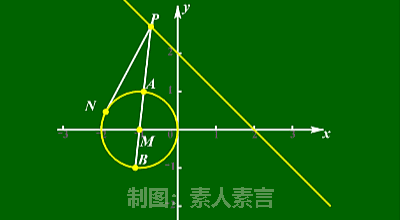
从动图不难看出，

在点P移动的过程中，

|PA|、|PB|的长度虽然都在不断变化，

但它们的比值却总是不变的。

定义三:

---

平面内到两定点的距离之比为定值(定值不为1)

的点的轨迹叫作圆。

这里的圆，

便是中考热点、高考难点的阿氏圆了。

有兴趣的同学或老师，

可以翻翻公众号里的这一篇：

“圆来如此，阿氏圆的深度学习”

(点击链接可查看)

典例解析：

---

根据阿氏圆特征，

阿氏圆的圆以必在线段BC延长线上。

既然都确实了满足条件的轨迹是圆，

当然是可以考虑取特殊位置的。

我在线段BC及延长线上，

分别取了点M、N，

且都满足|BM|=3|MC|,|BN|=3|NC|

那么再以MN为直径作圆，

便一定是阿氏圆了。

你能理解吗？

四个方程

---

根据已知条件特征的不同，

在求圆的方程时，

常有四种不同的表达方式。

标准式：

---

如果已知了圆心和半径，常用标准式来表示。

(x-a)²+(y-b)²=R²

一般式：

---

如果已知圆上的几个点，常用一般式来表示。

x²+y²+Dx+Ey+F=0

直径式：

---

如果已知直径的两个端点，常用直径式表示。

(x-x₁)(x-x₂)+(y-y₁)(y-y₂)=0

参数式：

圆系方程：

---

经过直线与圆交点的圆：

x²+y²+Dx+Ey+F+λ(ax+by+c)=0

经过两圆交点的圆：

x²+y²+D₁x+E₁y+F₁+λ(x²+y²+D₂x+E₂y+F₂)=0

典例解析：

---

特别说明：

根据需要，

有时是可以将点看成一个以0为半径的圆的。

所以，

第三种思路，

你是不是真的也能理解呢？

切线相关

---

切线定义：

---

如果一条直线与圆只有一个交点，则称直线与圆是相切的，这条直线叫圆的一条切线。

切线性质：

---

圆的任意一条切线均垂直于切点与圆心连线。

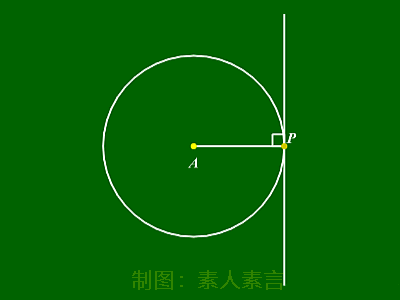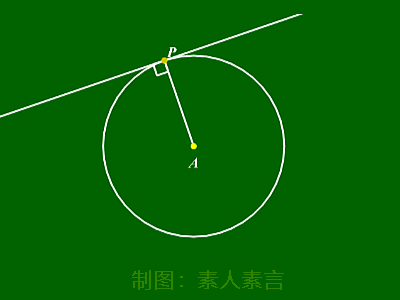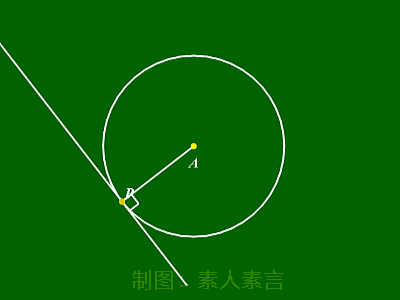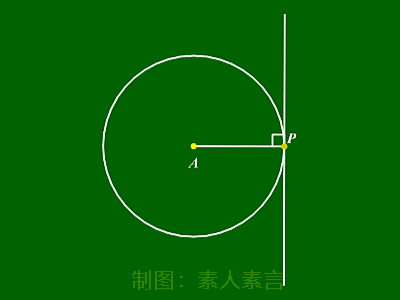
切线长：

---

①切线长定义：

过圆外一点向圆引切线，切点与该点之间的距离，

称为切线长。

②切线长度：

切线方程：

---

①求过圆上一点P(x₀,y₀)的圆的切线方程：

    先求切点与圆心连线斜率k.

❶ 若k不存在，

    由图形直接写出切线方程：y=y₀

❷ 若k=0，

    由图直接写出切线方程：x=x₀

❸ 其它：

     由垂直关系得切线斜率，由点斜率式写切线

     方程。 或者根据直线与圆的交点个数，用

     待定系数法。

客观题，

一定是可以直接用下面结论的：

将平方项及一次项分别改写得切线方程。

改写标准：平方改成积，一次方改成平均数。

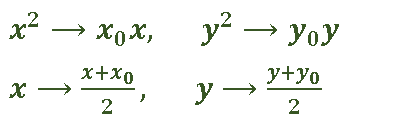
特别说明(圆的极点极线)

---

按照以上方式改写，所得直线几何意义为：

①若点Ｐ在圆上：直线为切线；

②若点Ｐ在圆外：直线为切点弦所在直线；

③若点Ｐ在圆内：直线为过该点的弦端点处切线

                             交点轨迹。

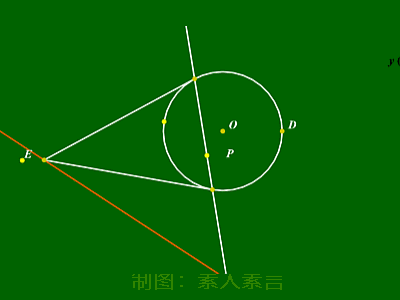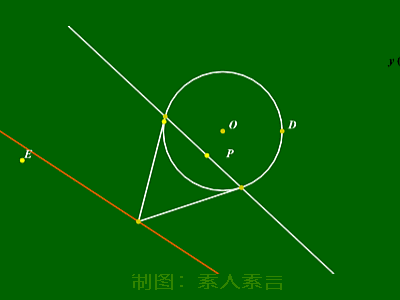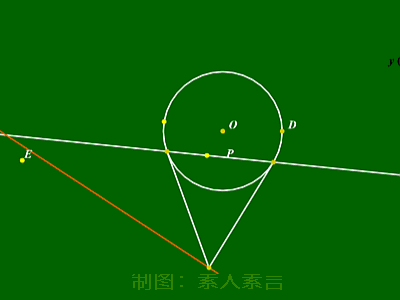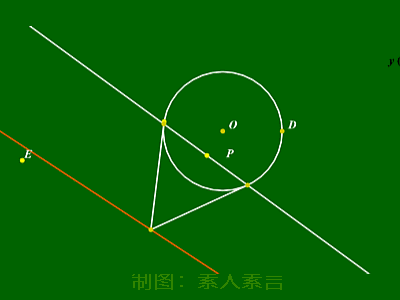
典例解析：

---

其实，

从上面的解法不难看出，

解析几何毕竟首先是几何，

所以解题思路的分析,

首先还是要从，

几何图形或几何性质上着手，

这样可以在一定程度上优化计算过程。

当然，

代数法虽然计算量很大，

但因为思路简洁，

也不失为一种比较理想的解法的。

1

②求过圆外一点P(x₀,y₀)的圆的切线方程

❶几何法：当斜率存在时，

　　　　　设直线方程为：y=k(x-x₀)+y₀

                     _{由圆心到直线距离等于半径求得k值，}

                  从而求出切线方程。

❷ 代数法：当斜率存在时，

　　　　　   设直线方程为：y=k(x-x₀)+y₀

                       _{代入圆的方程，得到关于x的一}

                    _{元二次方程，再由Δ=0，求得}

                    _{切线的斜率及方程。}

 _{典例解析：}

---

弦长相关

---

弦的定义：

---

圆周上任意两点的连线段，称为圆的一条弦。

垂径定理：

---

弦的中点与圆心的连线垂直平分弦。

弦长计算：

---

①代数法：

②几何法：

弦的最值：

---

过圆内一点，作圆的弦。

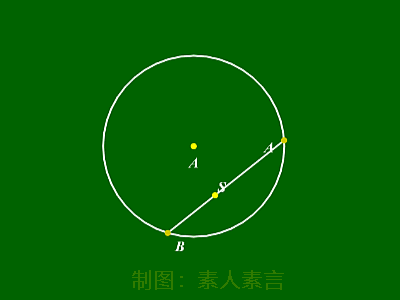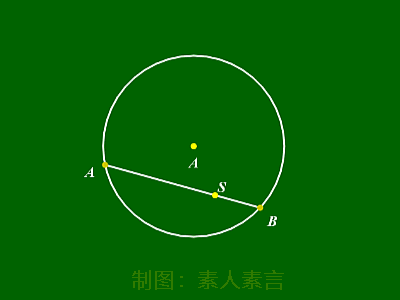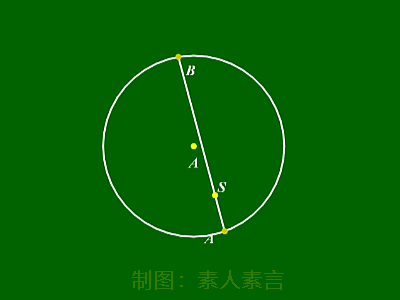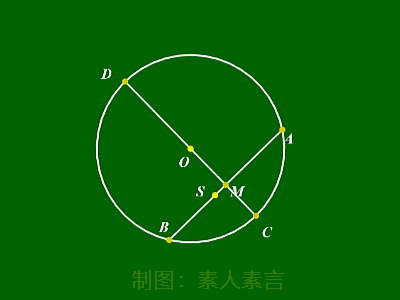
此时，从图中可以看出：

①最长弦为直径。

②最短弦为垂直于该直径的弦。

位置关系

直线与圆

相离

圆心到直线距离大于半径

方程组无解

相交

圆心到直线距离小于半径

方程组有

两组不同解

相切

圆心到直线距离等于半径

方程组有

两组相同解

▼

圆与圆

相离

圆心距大于半径之和

方程组无解

相交

圆心距小于半径之和

大于半径之差

方程组有

两组不同解

相切

圆心距等于半径之和

或半径之差

圆方程组有

两组相同解

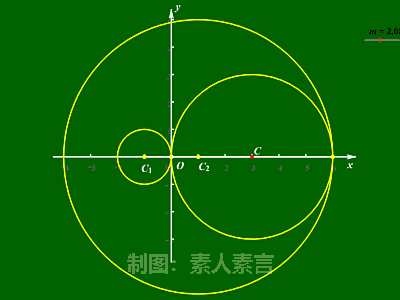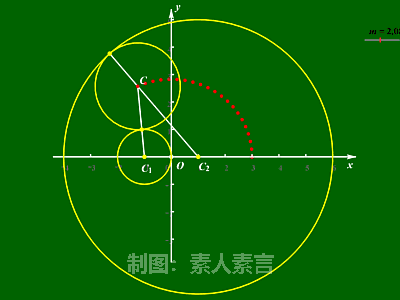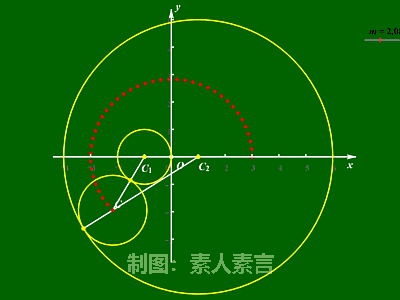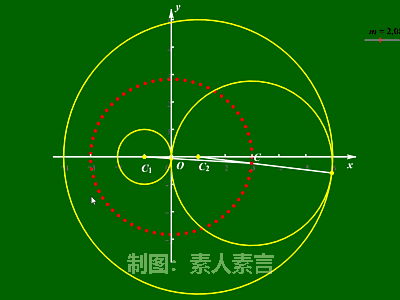
典例解析：

---

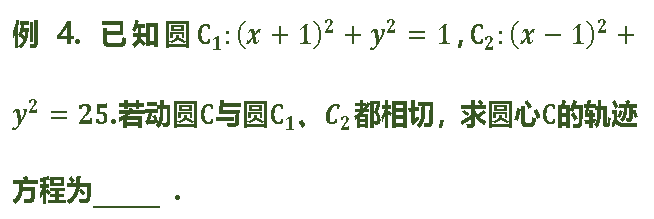
角 相 关

---

①直径所对的圆周长为90°；

---

∠BPA=90°

②内接四边形对角互补，

    任意外角等于其所对内对角；

---

∠BAD+∠BCD=180°

③同弦或等弦所对圆周角相等，

    圆心角是圆周角的二倍；

---

∠AMB=∠ANB,∠AOB=2∠ANB

④弦切角等于弦所对圆周角。

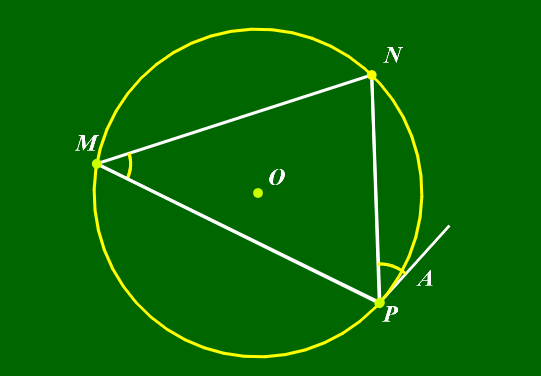
∠APN=∠PMN

几个定理

---

相交弦定理：▼

---

|AM|·|BM|=|CM|·|DM|

切割线定理：▼

---

|PA|²=|PB|·|PC|

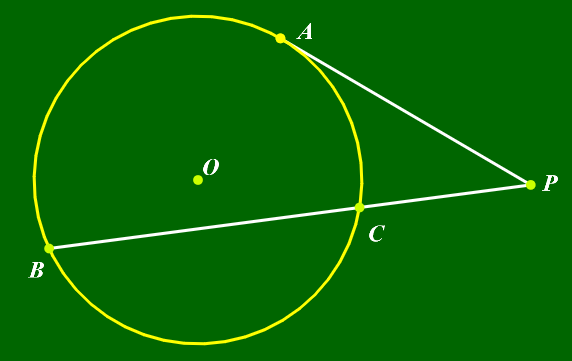
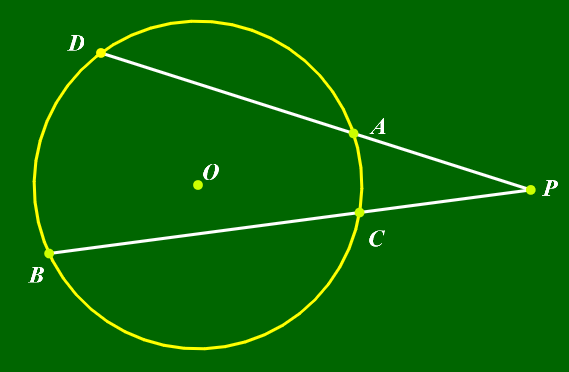
割线定理：▼

---

|PA|·|PD|=|PB|·|PC|

典例解析：

---