下面是从网上找的模板根据我自己的函数又改的,在运行的时候程序报错了,本人小白看不太懂,求各位大神解答一下,万分感谢!
function [best_x,best_fx,count]=dfp(x0,ess)
syms x1 x2 x3 t;
f=(x1^2+x2^2+x3^2-1183.215957^2)^2+(x1^2+(x2-1000)^2+x3^2-1095.445115^2)^2+((x1-500)^2+x2^2+x3^2-1204.159458^2)^2+((x1-500)^2+(x2-1000)^2+x3^2-1118.033989^2)^2;
fx=diff(f,x1);%求表达式f对x1的一阶求导
fy=diff(f,x2);%求表达式f对x2的一阶求导
fz=diff(f,x3);%求表达式f对x3的一阶求导
fi=[fx fy fz];%构造函数f的梯度函数
%初始点的梯度和函数值
g0=subs(fi,[x1 x2 x3],x0);
f0=subs(f,[x1 x2 x3],x0);
H0=eye(3);
%输出x0,f0,g0
x0
f0
g0
xk=x0;
fk=f0;
gk=g0;
Hk=H0;
k=1;
while(norm(gk)>ess)%迭代终止条件||gk||<=ess
disp('************************************************************')
disp(['第' num2str(k) '次寻优'])
%确定搜索方向
pk=-Hk*gk';
%由步长找到下一点x(k+1)
xk=xk+t*pk';
f_t=subs(f,[x1 x2 x3],xk); %构造一元搜索的一元函数φ(t)
%由一维搜索找到最优步长
df_t=diff(f_t,t);
tk=solve(df_t);
if tk~=0
tk=double(tk);
else
break;
end
%计算下一点的函数值和梯度
xk=subs(xk,t,tk)
fk=subs(f,[x1 x2 x3],xk)
gk0=gk;
gk=subs(fi,[x1 x2 x3],xk)
%DPF校正公式,找到修正矩阵
yk=gk-gk0;
sk=tk*pk';
Hk=Hk-(Hk*yk'*yk*Hk)/(yk*Hk*yk')+sk'*sk/(yk*sk')%修正公式
k=k+1;
end
disp('结果如下:')
best_x=xk;%最优点
best_fx=fk;%最优值
count=k-1;
命令窗输入
x0=[250 500 500];
ess=0.01;
[best_x,best_fx,count]=dfp(x0,ess)
报错画面:
2017-4-17 15:47 上传

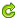
一
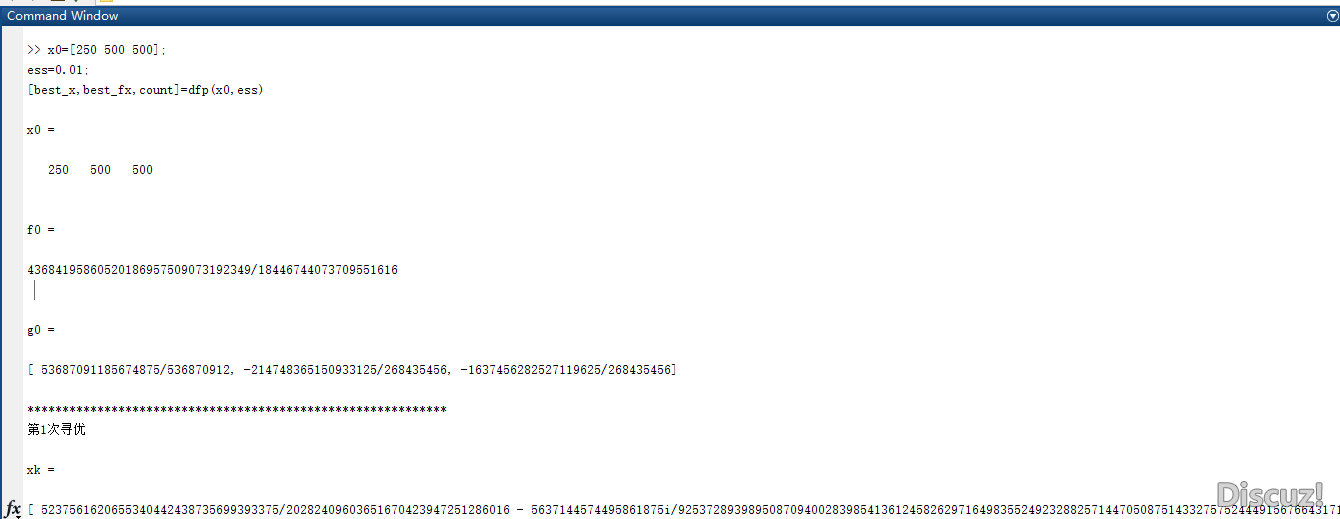
2017-4-17 15:47 上传

二





















 802
802











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








