两个集合根据属性取差集_python与集合

     集合，简称集，是数学中一个基本概念，也是集合论的主要研究对象。集合是“确定的一堆东西”，集合里的“东西”则称为元素。现代的集合一般被定义为：由一个或多个确定的元素所构成的整体。

集合满足的三个条件 1.不同元素组成 2.无序 3.集合中的元素必须是不可变类型

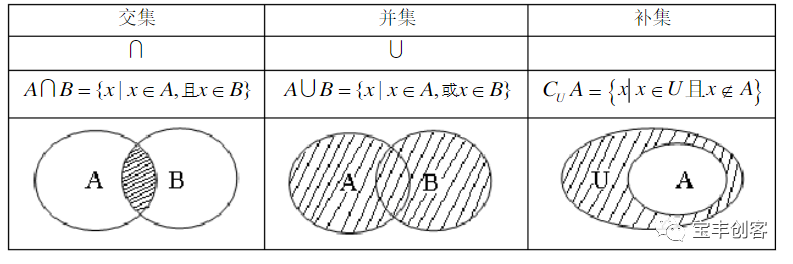
        集合是由不重复元素组成的无序的集。它的基本用法包括成员检测和消除重复元素。集合对象也支持像 联合，交集，差集，对称差分等数学运算。

在python中，集合set具有字典key的特点，其元素无序且唯一，可以通过大括号{}或者函数set来创建，需要注意一点，空的集合只可以通过set函数创建，因为单一的大括号用来表示空的字典。集合中元素是无序的，所以无法通过下标访问。

a = set('abracadabra')

b = set('alacazam')

print(a)                #可以看到集合元素的无序性，唯一性

print(b)                #{'m', 'l', 'z', 'a', 'c'}

print(a-b)            #取差集

print(b-a)            #取差集

print(a|b)             #取并集

print(a&b)           # 取交集

print(a^b)            #取a,b中独有元素的合集

同时，集合中的元素是可变的，可以增删改查。

c=set('123456')

c.add('7')

print(c)

c.remove('3')

print(c)

python中的set是可变序列，通过add等方法可以动态修改set中的内容，与之对应的，还有一种frozenset类型，顾名思义，是一种元素不可变的集合，其他特性和set完全相同，可以根据需要来选择set还是frozenset。

操作	等效运算	运算结果
len(s)		集合元素个数
x in s		判断元素x是否属于集合s
x not in s		判断元素x是否不属于集合s
s.issubset(t)	s <= t	测试集合s是否集合t的子集,或者说集合s包含于t
s.issuperset(t)	s >= t	测试集合s是否包含集合t
s.union(t)	s 此处竖杠 t	集合s与集合t的并集
s.intersection(t)	s & t	集合s与集合t的交集
s.difference(t)	s - t	集合s与集合t的差集
s.symmetric_difference(t)	s ^ t	集合s与t的对称差集,即那些既要么在s中要么在t中但是不同时在集合st的部分

可以参考我的例子，在网上试着运行自己的程序