二元函数最大最小值定理证明_2021考研数学 高数第3章 微分中值定理及导数应用...

目录

• 目录
• 1. 背景
• 2. 微分中值定理
  • 2.1. 费马引理
  • 2.2. 罗尔定理
  • 2.3. 拉格朗日中值定理
  • 2.4. 柯西中值定理
  • 2.5. 皮亚诺型余项泰勒公式
  • 2.6. 拉格朗日型余项泰勒公式
  • 2.7. 几个常用的泰勒公式（拉格朗日余项）
  • 2.8. 不等式的证明
• 3. 导数应用
  • 3.1. 函数的单调性
  • 3.2. 函数的极值
  • 3.3. 函数的最大值和最小值
  • 3.4. 曲线的凹凸性
  • 3.5. 曲线的渐近线
  • 3.6. 函数的作图
  • 3.7. 曲线的弧微分与曲率
• 4. 总结

---

1. 背景

前段时间复习完了高数第三章的内容，我参考《复习全书·基础篇》和老师讲课的内容对这一章的知识点进行了整理，形成了这篇笔记，方便在移动设备上进行访问和后续的补充修改。

2. 微分中值定理

2.1. 费马引理

设函数

在点

处可导，如果函数

在点

处取得极值，那么

.

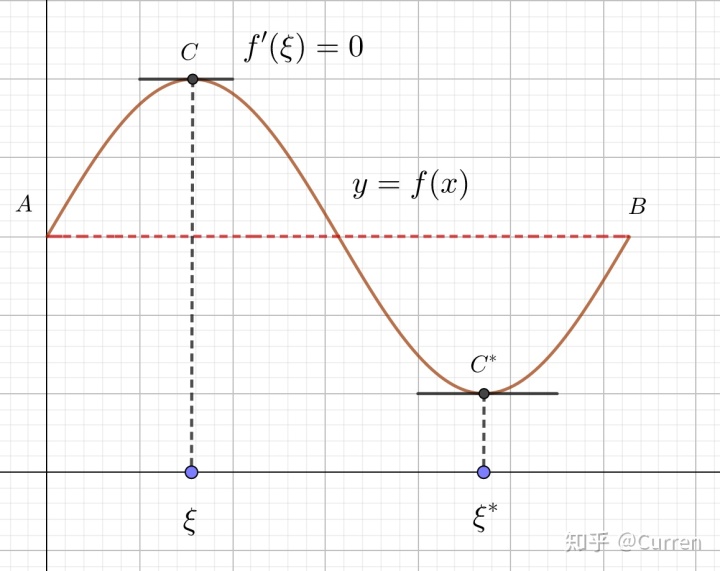
2.2. 罗尔定理

如果

满足以下条件

1. 在闭区间
   上连续
2. 在开区间
   内可导
3. ,

则在

内至少存在一点

，使得

.

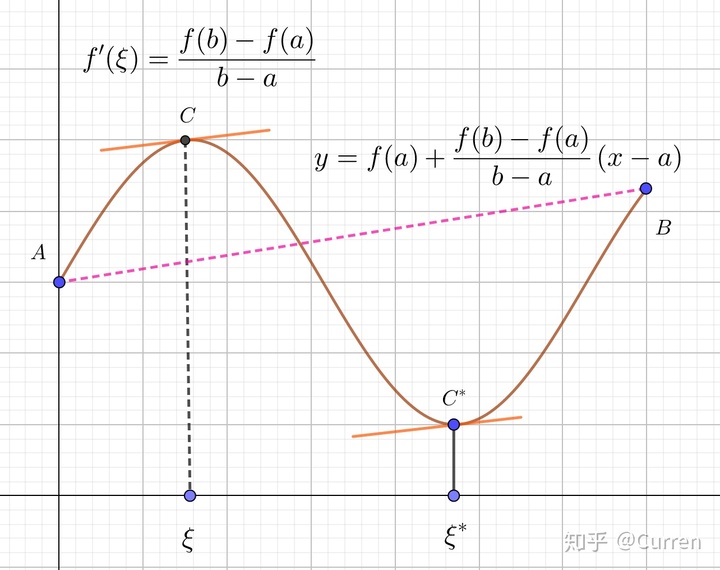
2.3. 拉格朗日中值定理

• 定义

如果

满足以下条件

1. 在闭区间
   上连续
2. 在开区间
   内可导，

则在

内至少存在一点

，使得

• 证明

已知函数在闭区间

上连续，在开区间

内可导，构造辅助函数

可得

，又因为

在

上连续，在开区间

内可导，所以根据罗尔定理可得必有一点

，使得